Saltar al contenido principal
LibreTexts Español

10.3: Principio de Arquímedes

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128473
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Calcular la dirección de la fuerza de flotabilidad

    Cuando te levantas de sumergirte en un baño tibio, tus brazos pueden sentirse extrañamente pesados. Este efecto se debe a la pérdida del soporte flotante del agua. ¿Qué crea esta fuerza de flotación? ¿Por qué es que algunas cosas flotan y otras no? ¿Los objetos que se hunden obtienen algún apoyo del fluido? ¿Tu cuerpo está impulsado por la atmósfera, o solo se ven afectados los globos de helio?

    Fuerza de flotación: causa y cálculo

    Encontramos las respuestas a las preguntas anteriores en el hecho de que en cualquier fluido dado, la presión aumenta con la profundidad. Cuando un objeto se sumerge en un fluido, la fuerza ascendente en la parte inferior de un objeto es mayor que la fuerza descendente en la parte superior del objeto. El resultado es una fuerza neta hacia arriba (una fuerza de flotación) sobre cualquier objeto en cualquier fluido. Si la fuerza de flotación es mayor que el peso del objeto, el objeto se elevará a la superficie y flotará. Si la fuerza de flotación es menor que el peso del objeto, el objeto se hundirá. Si la fuerza de flotación es igual al peso del objeto, el objeto permanecerá suspendido a esa profundidad. La fuerza de flotación siempre está presente en un fluido, ya sea que un objeto flote, se hunda o permanezca suspendido.

    La fuerza de flotación es resultado de la presión ejercida por el fluido. El fluido empuja en todos los lados de un objeto sumergido, pero a medida que la presión aumenta con la profundidad, el empuje es más fuerte en la superficie inferior del objeto que en la parte superior (como se ve en).

    Se puede calcular la fuerza de flotación sobre un objeto sumando las fuerzas ejercidas en todos los lados de un objeto. Por ejemplo, considere el objeto que se muestra en.

    La superficie superior tiene área\(\mathrm{A}\) y está en profundidad\(\mathrm{h_1}\); la presión a esa profundidad es:

    \[\mathrm{P_1=h_1ρg,}\]

    donde ρρ es la densidad del fluido y\(\mathrm{g≈9.81 \frac{m}{s^2}}\) es la aceleración gravitacional. La magnitud de la fuerza en la superficie superior es:

    \[\mathrm{F_1=P_1A=h_1ρgA.}\]

    Esta fuerza apunta hacia abajo. Del mismo modo, la fuerza sobre la superficie inferior es:

    \[\mathrm{F_2=P_2A=h_2ρgA}\]

    y apunta hacia arriba. Debido a que es cilíndrica, la fuerza neta en los lados del objeto es cero: las fuerzas en diferentes partes de la superficie se oponen entre sí y cancelan exactamente. Así, la fuerza neta hacia arriba sobre el cilindro debida al fluido es:

    \[\mathrm{F_B=F_2−F_1=ρgA(h_2−h_1)}\]

    El principio de Arquímedes

    Aunque calcular la fuerza de flotación de esta manera siempre es posible, muchas veces es muy difícil. Un método más sencillo se desprende del principio de Arquímedes, que establece que la fuerza de flotación ejercida sobre un cuerpo sumergido en un fluido es igual al peso del fluido que desplaza el cuerpo. Es decir, para calcular la fuerza de flotación sobre un objeto asumimos que la parte sumergida del objeto está hecha de agua y luego calcular el peso de esa agua (como se ve en).

    imagen

    Principio de Arquímedes: La fuerza de flotación sobre el buque (a) es igual al peso del agua desplazada por el buque, que se muestra como la región discontinua en (b).

    El principio se puede afirmar como una fórmula:

    \[\mathrm{F_B=w_{fl}}\]

    El razonamiento detrás del principio de Arquímedes es que la fuerza de flotación sobre un objeto depende de la presión ejercida por el fluido sobre su superficie sumergida. Imagínese que reemplazamos la parte sumergida del objeto con el fluido en el que está contenido, como en (b). La fuerza de flotabilidad sobre esta cantidad de fluido debe ser la misma que en el objeto original (el barco). No obstante, también sabemos que la fuerza de flotabilidad sobre el fluido debe ser igual a su peso, ya que el fluido no se hunde en sí mismo. Por lo tanto, la fuerza de flotabilidad sobre el objeto original es igual al peso del “fluido desplazado” (en este caso, el agua dentro de la región discontinua (b)).

    El principio de Arquímedes es válido para cualquier fluido, no solo líquidos (como el agua) sino también gases (como el aire). Exploraremos esto más a medida que discutamos las aplicaciones del principio en secciones posteriores.

    Principio de Arquímedes — Ejemplo simple: Utilizamos el Principio de Arquímedes para determinar el número de pingüinos que un flotador de hielo puede soportar secamente.

    Sumersión Completa

    La fuerza de flotabilidad sobre un objeto de volumen completamente sumergido es\(\mathrm{F_B=Vρg}\).

    objetivias de aprendizaje

    • Identificar los factores que determinan la fuerza de flotabilidad en un objeto completamente sumergido

    El principio de Arquímedes es más fácil de entender y aplicar en el caso de objetos totalmente sumergidos. En esta sección discutimos algunos ejemplos relevantes. En general, la fuerza de flotación sobre un objeto completamente sumergido viene dada por la fórmula:

    \[\mathrm{F_B=Vρg,}\]

    donde\(\mathrm{V}\) está el volumen del objeto,\(\mathrm{ρ}\) es la densidad del fluido, y\(\mathrm{g}\) es la aceleración gravitacional. Esto se desprende inmediatamente del principio de Arquímedes, y del hecho de que el objeto esté completamente sumergido (y así el volumen del fluido desplazado es solo el volumen del objeto).

    Cilindro

    En la sección anterior, calculamos la fuerza de flotabilidad sobre un cilindro (mostrada en) considerando la fuerza ejercida en cada uno de los lados del cilindro. Ahora, calcularemos esta fuerza usando el principio de Arquímedes. La fuerza de flotabilidad en el cilindro es igual al peso del fluido desplazado. Este peso es igual a la masa del fluido desplazado multiplicada por la aceleración gravitacional:

    imagen

    Fuerza de flotación: El fluido empuja en todos los lados de un objeto sumergido. Sin embargo, debido a que la presión aumenta con la profundidad, el empuje hacia arriba en la superficie inferior (F2) es mayor que el empuje hacia abajo en la superficie superior (F1). Por lo tanto, la fuerza neta de flotación es siempre hacia arriba.

    \[\mathrm{F_B=w_{fl}=m_{fl}g}\]

    La masa del fluido desplazado es igual a su volumen multiplicado por su densidad:

    \[\mathrm{m_{fl}=V_{fl}ρ}\]

    Sin embargo (y este es el punto crucial), el cilindro está completamente sumergido, por lo que el volumen del fluido desplazado es solo el volumen del cilindro (ver), y:

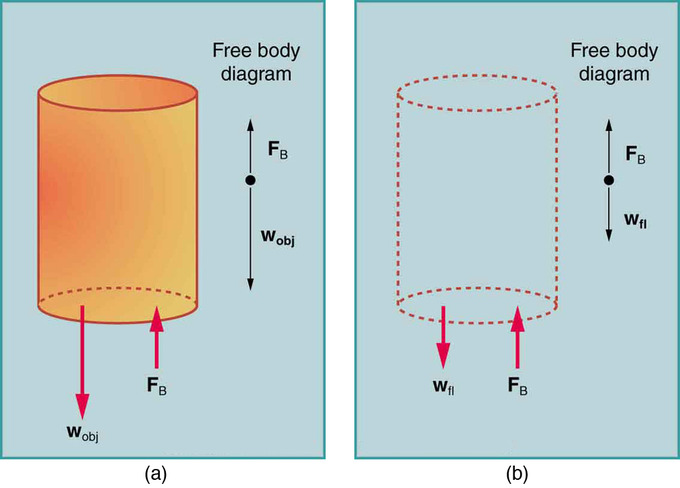
    imagen

    Principio de Arquímedes: El volumen del fluido desplazado (b) es el mismo que el volumen del cilindro original (a).

    \[\mathrm{m_{fl}=V_{fl}ρ=V_{cylinder}ρ.}\]

    El volumen de un cilindro es el área de su base multiplicada por su altura, o en nuestro caso:

    \[\mathrm{V_{cylinder}=A(h_2−h_1).}\]

    Por lo tanto, la fuerza de flotabilidad en el cilindro es:

    \[\mathrm{F_B=m_{fl}g=V_{cylinder}ρg=(h_1−h_2)ρgA.}\]

    Este es el mismo resultado obtenido en la sección anterior al considerar la fuerza debida a la presión ejercida por el fluido.

    Difusor de helio

    Considere el USS Macon, un dirigible lleno de helio (mostrado en). Su envoltura (el “globo”) contenía 184,059.5 metros cúbicos de helio. Ignorando el pequeño volumen de la góndola, ¿cuál era la fuerza de flotabilidad en esta aeronave? Si el dirigible pesaba 108,000 kg, ¿cuánta carga podría llevar? Supongamos que la densidad del aire es de 1.225 kg por metro en cubos. La fuerza de flotabilidad en una aeronave se debe al aire en el que se encuentra inmersa. Aunque desconocemos la forma exacta de la aeronave, conocemos su volumen y la densidad del aire, y así podemos calcular la fuerza de flotabilidad:

    imagen

    Diaereador de helio: El USS Macon, un dirigible lleno de helio de los años treinta.

    \[\mathrm{F_B=V_{ρg}=184,059.5 \; kg \times 1.225 \dfrac{kg}{m^3} \times 9.81 \dfrac{m}{s^2}≈2.212 \times 10^6 \; N}\]

    Para encontrar la capacidad de carga de la aeronave, restamos el peso de la aeronave a la fuerza de flotabilidad:

    \[\mathrm{F_{cargo}=F_B−mg=2.21 \times 10^6 \; N−1.08 \times 10^5 \; kg \times 9.81 \dfrac{m}{s^2}=1.15 \times 10^6 \; N}\]

    La masa que puede llevar la aeronave es:

    \[\mathrm{m_{cargo}=\dfrac{F_{cargo}}{g}=1.2 \times 10^5 \; kg= 120 \; tons.}\]

    Flotación

    Un objeto flota si la fuerza de flotación ejercida sobre él por el fluido equilibra su peso.

    objetivos de aprendizaje

    • Expresar la relación entre la fuerza de flotabilidad y el peso de un objeto flotante

    ¿Por qué flotan algunos objetos, pero otros no? Si pones una moneda de metal en un vaso de agua se hundirá. Pero la mayoría de los barcos están construidos de metal, y flotan. Entonces, ¿cómo es esto posible?

    Condición para flotación

    Un objeto flotará si la fuerza de flotación ejercida sobre él por el fluido equilibra su peso, es decir, si FB=MGFB=Mg.

    Pero el principio de Arquímedes establece que la fuerza de flotación es el peso del fluido desplazado. Entonces, para un objeto flotante sobre un líquido, el peso del líquido desplazado es el peso del objeto. Así, sólo en el caso especial de flotación la fuerza de flotación que actúa sobre un objeto es igual al peso del objeto. Considera un bloque de hierro sólido de una tonelada. Como el hierro es casi ocho veces más denso que el agua, desplaza solo 1/8 tonelada de agua cuando se sumerge, lo que no es suficiente para mantenerlo a flote. Supongamos que el mismo bloque de hierro se transforma en un tazón. Aún pesa una tonelada, pero cuando se pone en agua, desplaza un mayor volumen de agua que cuando era una cuadra. Cuanto más profundo se sumerge el cuenco de hierro, más agua desplaza, y mayor es la fuerza de flotación que actúa sobre él. Cuando la fuerza de flotación sea igual a una tonelada, no se hundirá más.

    Cuando cualquier barco desplaza un peso de agua igual a su propio peso, flota. Esto suele llamarse el “principio de flotación” donde un objeto flotante desplaza un peso de fluido igual a su propio peso. Cada barco, submarino y dirigible debe estar diseñado para desplazar un peso de fluido igual a su propio peso. Un barco de 10,000 toneladas debe construirse lo suficientemente ancho como para desplazar 10,000 toneladas de agua antes de que se hunda demasiado en el agua. Lo mismo ocurre con los buques en el aire (ya que el aire es un fluido): Un dirigible que pesa 100 toneladas desplaza al menos 100 toneladas de aire; si desplaza más, sube; si desplaza menos, cae. Si el dirigible desplaza exactamente su peso, flota a una altitud constante.

    Flotación y Densidad

    La densidad juega un papel crucial en el principio de Arquímedes. La densidad promedio de un objeto es lo que determina en última instancia si flota. Si su densidad promedio es menor que la del fluido circundante, flotará. Esto se debe a que el fluido, al tener una mayor densidad, contiene más masa y por lo tanto más peso en el mismo volumen. La fuerza de flotación, que equivale al peso del fluido desplazado, es así mayor que el peso del objeto. De igual manera, un objeto más denso que el fluido se hundirá. La medida en que se sumerge un objeto flotante depende de cómo se relaciona la densidad del objeto con la del fluido. Por ejemplo, un buque descargado tiene una densidad menor, y menos de él está sumergido en comparación con el mismo barco cargado con carga. Podemos derivar una expresión cuantitativa para la fracción sumergida considerando la densidad. La fracción sumergida es la relación entre el volumen sumergido y el volumen del objeto, o

    imagen

    Densidad e Sumersión: Un buque descargado (a) flota más alto en el agua que un barco cargado (b).

    \[\mathrm{fraction \; submerged=\dfrac{V_{sub}}{V_{obj}}=\dfrac{V_{fl}}{V_{obj}}}\]

    El volumen sumergido equivale al volumen de fluido desplazado, al que llamamos\(\mathrm{V_{fl}}\). Ahora podemos obtener la relación entre las densidades sustituyéndolo\(\mathrm{ρ=mV}\) en la expresión. Esto da

    \[\mathrm{fraction \; submerged=\dfrac{m_{fl}/ρ_{fl}}{m_{obj}/ \bar{ρ}_{obj}}}\]

    donde\(\mathrm{\bar{ρ}_{obj}}\) es la densidad promedio del objeto y ρflρflis la densidad del fluido. Dado que el objeto flota, su masa y la del fluido desplazado son iguales, y así cancelan de la ecuación, dejando

    \[\mathrm{fraction \; submerged=\dfrac{\bar{ρ}_{obj}}{ρ_{fl}.}}\]

    Hay un par de cosas a tener en cuenta sobre esta expresión:

    1. Tenga en cuenta que menciona la densidad promedio del objeto. Esto puede ser mucho menor que la densidad del material del que está hecho el objeto. Por ejemplo, un barco de acero en realidad está mayormente lleno de aire (piense en los pasillos, bodegas de carga, etc.), por lo que su densidad promedio se encuentra entre la del aire y el acero. Para ser más precisos, la densidad promedio se define como la masa total de un objeto dividida por su volumen total:\(\mathrm{\bar{ρ}=\frac{m}{V}.}\)
    2. Esta fórmula sólo tiene sentido si la densidad del objeto es menor que la densidad del fluido. De lo contrario, la fracción sumergida se vuelve mayor que una, ¡una señal de que el objeto no flota en absoluto, sino que se hunde!

    Puntos Clave

    • La fuerza de flotabilidad es causada por la presión ejercida por el fluido en el que se sumerge un objeto.
    • La fuerza de flotabilidad siempre apunta hacia arriba porque la presión de un fluido aumenta con la profundidad.
    • Se puede calcular la fuerza de flotabilidad ya sea directamente calculando la fuerza ejercida sobre cada una de las superficies del objeto, o indirectamente encontrando el peso del fluido desplazado.
    • Si un objeto está completamente sumergido, el volumen del fluido desplazado es igual al volumen del objeto.
    • La fuerza de flotabilidad sobre globos aerostáticos, dirigibles y otros objetos se puede calcular asumiendo que están completamente sumergidos en el aire.
    • La fuerza de flotabilidad no depende de la forma del objeto, sólo de su volumen.
    • La fuerza de flotabilidad que experimenta un objeto depende de su forma.
    • La fracción del volumen de un objeto que está sumergido viene dada por la relación entre su densidad promedio y la del fluido:\(\mathrm{\frac{\bar{ρ}_{obj}}{ρ_{fl}}}\).
    • Un objeto flota si la fuerza de flotación ejercida sobre él por el fluido equilibra su peso.

    Términos Clave

    • fuerza de flotación: Fuerza ascendente ejercida por un fluido que se opone al peso de un objeto sumergido.
    • Principio de Arquímedes: La fuerza de flotación ejercida sobre un cuerpo sumergido en un fluido es igual al peso del fluido que desplaza el cuerpo.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 10.3: Principio de Arquímedes is shared under a not declared license and was authored, remixed, and/or curated by Boundless.