10.6: Deformación de Sólidos

Última actualización
Guardar como PDF

Page ID: 128462

Boundless
Boundless

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Objetivos de aprendizaje

Explicar cómo se determina la longitud de un objeto

Largo

En las medidas geométricas, la longitud es la dimensión más larga de un objeto. En otros contextos “longitud” es la dimensión medida de un objeto. Por ejemplo: es posible cortar una longitud de un alambre que sea más corta que el grosor del alambre. La longitud se puede distinguir de la altura, que es la extensión vertical, y la anchura o anchura, que son la distancia de lado a lado, midiendo a través del objeto en ángulo recto con la longitud.

La longitud es una medida de una dimensión, mientras que el área es una medida de dos dimensiones (longitud cuadrada) y el volumen es una medida de tres dimensiones (longitud en cubos). En la mayoría de los sistemas de medición, la unidad de longitud es una unidad fundamental, a partir de la cual se definen otras unidades.

Después de la Teoría de la Relatividad Especial de Albert Einstein, ya no se puede pensar que la longitud sea constante en todos los marcos de referencia. Por lo tanto, una regla de un metro de largo en un marco de referencia no tendrá un metro de largo en un marco de referencia que se desplaza a una velocidad relativa al primer fotograma. Esto significa que la longitud de un objeto es variable dependiendo del observador.

Unidades

Una de las unidades de medida de longitud más antiguas utilizadas en el mundo antiguo fue el 'codo ', que era la longitud del brazo desde la punta del dedo hasta el codo. Esto podría entonces subdividirse en unidades más cortas como el pie, la mano (que a las 4 pulgadas todavía se usa hoy en día para expresar la altura de los caballos) o el dedo, o agregarse para hacer unidades más largas como la zancada. El codo podría variar considerablemente debido a los diferentes tamaños de personas.

En las ciencias físicas y la ingeniería, cuando se habla de “unidades de longitud”, la palabra “longitud” es sinónimo de “distancia”. Existen varias unidades que se utilizan para medir la longitud. Las unidades de longitud pueden basarse en longitudes de partes del cuerpo humano, la distancia recorrida en varios pasos, la distancia entre hitos o lugares en la Tierra, o arbitrariamente en la longitud de algún objeto fijo.En el Sistema Internacional de Unidades (SI), la unidad básica de longitud es el metro y ahora se define en términos de la velocidad de la luz. El centímetro y el kilómetro, derivados del medidor, también son unidades de uso común. En las unidades habituales de Estados Unidos, inglés o sistema imperial de unidades, las unidades de longitud comúnmente utilizadas son la pulgada, el pie, el patio y la milla. Las unidades utilizadas para denotar distancias en la inmensidad del espacio, como en la astronomía, son mucho más largas que las utilizadas típicamente en la Tierra e incluyen la unidad astronómica, el año luz y el pársec.

imagen

Longitud: La longitud métrica de un kilómetro es equivalente a la medida imperial de 0.62137 millas.

Forma

La forma de un objeto es una descripción del espacio que ocupa el objeto; la forma puede cambiar si el objeto se deforma.

objetivos de aprendizaje

Describir los efectos de las deformaciones, rotaciones y aumentos

Forma

La forma de un objeto ubicado en algún espacio es una descripción geométrica de la parte de ese espacio ocupada por el objeto, según lo determinado por su límite externo, abstrayendo de la ubicación y orientación en el espacio, el tamaño y otras propiedades como el color, el contenido y la composición del material

Formas simples y complejas

Las formas simples se pueden describir mediante objetos de geometría básica como un conjunto de dos o más puntos, una línea, una curva, un plano, una figura plana (por ejemplo, cuadrado o círculo) o una figura sólida (por ejemplo, cubo o esfera). La mayoría de las formas que ocurren en el mundo físico son complejas. Algunas, como las estructuras vegetales y las costas, pueden ser tan arbitrarias que desafían la descripción matemática tradicional, en cuyo caso pueden analizarse por geometría diferencial, o como fractales.

En geometría, dos subconjuntos de un espacio euclidiano tienen la misma forma si uno puede transformarse al otro mediante una combinación de traslaciones, rotaciones (juntas también llamadas transformaciones rígidas) y escalados uniformes. En otras palabras, la forma de un conjunto de puntos es toda la información geométrica que es invariante a las traslaciones, rotaciones y cambios de tamaño. Tener la misma forma es una relación de equivalencia, y en consecuencia se puede dar una definición matemática precisa de la noción de forma como una clase de equivalencia de subconjuntos de un espacio euclidiano que tiene la misma forma.

Las formas de los objetos físicos son iguales si los subconjuntos de espacio que ocupan estos objetos satisfacen la definición anterior. En particular, la forma no depende del tamaño y la colocación en el espacio del objeto.

imagen

Formas: Ejemplos de formas.

Volumen

El volumen es una medida del espacio tridimensional que ocupa un objeto, generalmente tomado en términos de longitud, anchura y altura.

objetivos de aprendizaje

Explicar cómo se mide el volumen geométricamente

Volumen es la cantidad de espacio tridimensional contenido por un límite cerrado; es el espacio que ocupa o contiene una sustancia (sólida, líquida, gas o plasma) o forma. El volumen a menudo se cuantifica numéricamente usando una unidad derivada del SI, el metro cúbico. No obstante, para los líquidos la unidad de volumen utilizada se conoce como el litro (equivalente a 0.001 metros cúbicos).

imagen

Volumen de medición: Se puede usar una taza medidora para medir volúmenes de líquidos. Esta copa mide el volumen en unidades de tazas, onzas líquidas y mililitros.

El volumen se mide geométricamente multiplicando las tres dimensiones de un objeto, generalmente tomadas como longitud, ancho y alto. Algunos volúmenes comunes se toman de la siguiente manera:

El volumen de un cubo: largo por ancho por alto.
El volumen de un cilindro: el área de la sección transversal multiplicada por la altura del cilindro.
El volumen de una esfera: 4/3 veces el radio cúbico por pi.

El volumen de un sólido puede ser determinado por el volumen de líquido que desplaza cuando se sumerge.

El volumen de un contenedor se entiende generalmente como la capacidad del contenedor, es decir, la cantidad de fluido (gas o líquido) que el contenedor puede contener, en lugar de la cantidad de espacio que desplaza el propio contenedor. Las tazas medidoras, como se ve en, funcionan tomando un área de sección transversal conocida de una taza y multiplicando esa por una altura variable. Dado que el líquido siempre cubrirá la sección transversal (si hay suficiente líquido), agregar más líquido aumentará la altura dentro del contenedor.

Los líquidos toman la forma de su contenedor, llenando la altura mínima necesaria. Los gases, por otro lado, ocupan la máxima cantidad de volumen posible. Así, una taza medidora puede medir con precisión el volumen de un líquido, mientras que un gas siempre llenará todo el contenedor, de manera más o menos uniforme, sin importar cuán poco gas haya.

Estrés y tensión

Una carga puntual crea un campo eléctrico que se puede calcular usando la Ley de Coulomb.

El campo eléctrico de una carga puntual es, como cualquier campo eléctrico, un campo vectorial que representa el efecto que la carga puntual tiene sobre otras cargas a su alrededor. El efecto se siente como una fuerza y cuando las partículas cargadas no están en movimiento esta fuerza se conoce como la fuerza electrostática. La fuerza electrostática es, al igual que la gravedad, una fuerza que actúa a distancia. Por lo tanto, racionalizamos esta acción a distancia diciendo que los cargos crean campos a su alrededor que tienen efectos en otros cargos.

Dada una carga puntual, o una partícula de tamaño infinitesimal que contiene cierta carga, las líneas de campo eléctrico emanan radialmente en todas las direcciones. Si la carga es positiva, las líneas de campo apuntan radialmente lejos de ella; si la carga es negativa, las líneas de campo apuntan radialmente hacia ella.

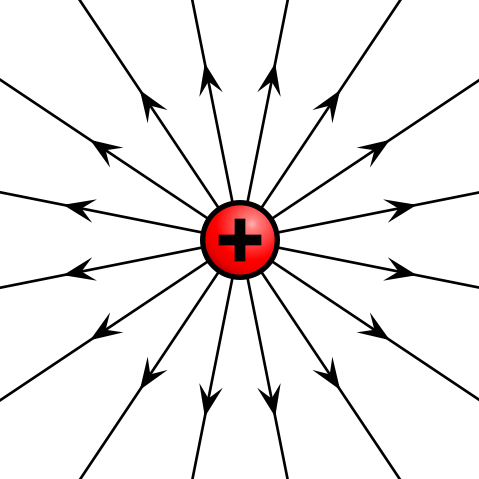
imagen

Campo eléctrico de carga puntual positiva: El campo eléctrico de una partícula cargada positivamente apunta radialmente lejos de la carga.

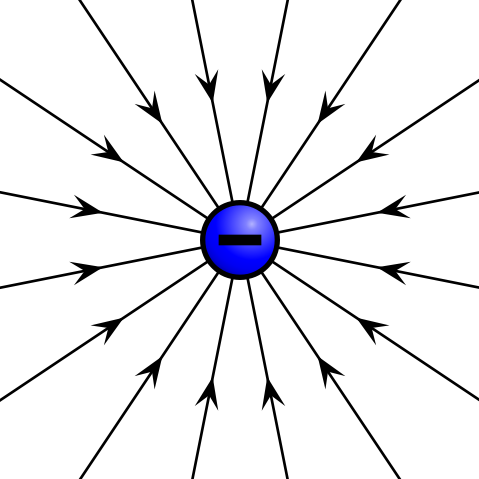
imagen

Campo eléctrico de carga de punto negativo: El campo eléctrico de una partícula cargada negativamente apunta radialmente hacia la partícula.

El motivo de estas direcciones se puede ver en la derivación del campo eléctrico de una carga puntual. Primero echemos un vistazo a la definición de campo eléctrico de una partícula puntual:

\[\mathrm{\overrightarrow{E}=\dfrac{1}{4πϵ_o}\dfrac{q}{r^2} \hat{r}=k\dfrac{q}{r^2} \hat{r}.}\]

En la ecuación anterior, q representa la carga de la partícula que crea el campo eléctrico y la constante k es el resultado de simplemente agrupar las constantes juntas. Esta carga es positiva o negativa. Si la carga es positiva, como se muestra arriba, el campo eléctrico estará apuntando en una dirección radial positiva desde la carga q (lejos de la carga) y el siguiente texto explica por qué. La ecuación anterior se define en coordenadas radiales que se pueden ver en.

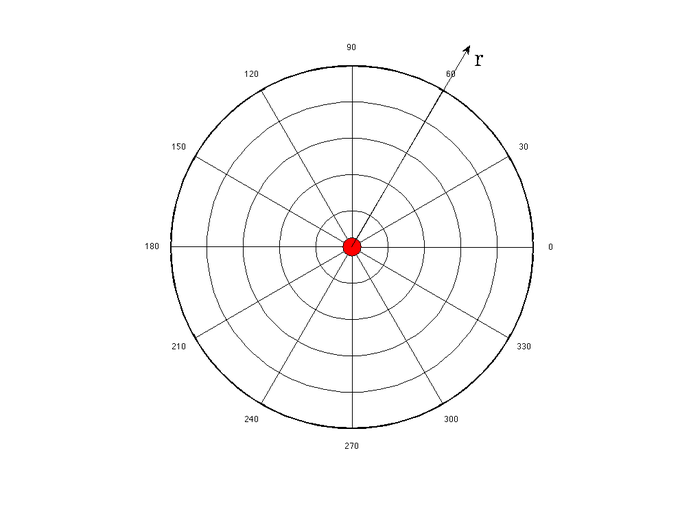
imagen

Sistema de coordenadas radiales: El campo eléctrico de una carga puntual se define en coordenadas radiales. La dirección r positiva apunta lejos del origen, y la dirección r negativa apunta hacia el origen. El campo eléctrico de una carga puntual es simétrico con respecto a la dirección θ.

Si ahora colocamos otra carga positiva, Q (llamada carga de prueba), a cierta distancia radial, R, lejos de la partícula original, la carga de prueba sentirá una fuerza dada por

\[\mathrm{\overrightarrow{F}=Q\overrightarrow{E}=Q\dfrac{1}{4πϵ_o}\dfrac{q}{R^2}\hat{r}}\]

Lo que hay que tener en cuenta es que la fuerza anterior está actuando sobre la carga de prueba Q, en la dirección radial positiva definida por la carga original q. Esto significa que debido a que las cargas son ambas positivas y se repelen entre sí, la fuerza sobre la carga de prueba apunta lejos de la carga original.

Si la carga de prueba fuera negativa, la fuerza que se siente sobre esa carga sería

\[\mathrm{\overrightarrow{F}=Q\overrightarrow{E}=-Q\dfrac{1}{4πϵ_o}\dfrac{q}{R^2}\hat{r}}\]

Observe que esto apunta en la\(\mathrm{\hat{r}}\) dirección negativa, que es hacia la carga original. Esto tiene sentido porque las cargas opuestas se atraen y la fuerza sobre la carga de prueba tenderá a empujarla hacia la carga positiva original creando el campo. La descripción matemática anterior del campo eléctrico de una carga puntual se conoce como Ley de Coulomb.

Puntos Clave

La longitud suele ser una medida de la dimensión más larga de un objeto.
La deformación de un objeto suele ser un cambio de longitud.
La unidad SI de longitud es el metro.
La forma de un objeto es una representación del espacio ocupado por el objeto.
Las deformaciones pueden cambiar la forma de un objeto.
Los objetos que tienen la misma forma se pueden transformar entre sí por rotación o aumento.
El volumen a menudo se cuantifica numéricamente usando una unidad derivada del SI, el metro cúbico. No obstante, para los líquidos la unidad de volumen utilizada se conoce como el litro (equivalente a 0.001 metros cúbicos).
Esto también puede entenderse como la cantidad de fluido que desplaza un objeto sumergido.
El volumen se puede medir para objetos geométricamente regulares mediante fórmulas simples. Sin embargo, los objetos más complicados son más fáciles de medir con el desplazamiento del fluido.
El campo eléctrico es un campo vectorial alrededor de una partícula cargada que representa la fuerza que otras partículas cargadas sentirían cuando se colocan cerca de la partícula creando el campo eléctrico.
Dada una carga puntual, o una partícula de tamaño infinitesimal, que contiene cierta carga, las líneas de campo eléctrico emanan por igual en todas las direcciones radiales.
Si la carga puntual es positiva, las líneas de campo apuntan lejos de ella; si la carga es negativa, las líneas de campo apuntan hacia ella.

Términos Clave

dimensión: Una medida de extensión espacial en una dirección particular, como la altura, anchura o anchura, o profundidad.
relatividad especial: Una teoría que (descuidando los efectos de la gravedad) reconcilia el principio de relatividad con la observación de que la velocidad de la luz es constante en todos los marcos de referencia.
plano: Una superficie nivelada o plana.
Euclidiana: Adherirse a los principios de la geometría tradicional, en la que las líneas paralelas son equidistantes.
sección transversal: Una sección formada por un plano que corta a través de un objeto, generalmente en ángulo recto con un eje.
dimensión: Una medida de extensión espacial en una dirección particular, como la altura, anchura o anchura, o profundidad.
ley del culombio: la ecuación matemática que calcula el vector de fuerza electrostática entre dos partículas cargadas
campo vectorial: una construcción en la que cada punto de un espacio euclidiano está asociado a un vector; una función cuyo rango es un espacio vectorial

Search

Text Color

Text Size

Margin Size

Font Type