Saltar al contenido principal
LibreTexts Español

12.3: Expansión Térmica

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128304
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Describir los cambios de volumen que ocurren en respuesta a un cambio de temperatura

    La expansión térmica es la tendencia de la materia a cambiar de volumen en respuesta a un cambio de temperatura. (Un ejemplo de esto es el pandeo de la vía del ferrocarril, como se ve en.) Los átomos y moléculas en un sólido, por ejemplo, oscilan constantemente alrededor de su punto de equilibrio. Este tipo de excitación se llama movimiento térmico. Cuando se calienta una sustancia, sus partículas constituyentes comienzan a moverse más, manteniendo así una mayor separación promedio con sus partículas vecinas. El grado de expansión dividido por el cambio de temperatura se denomina coeficiente de expansión térmica del material; generalmente varía con la temperatura.

    imagen

    Fig. 1: La expansión térmica de las secciones largas y continuas de las vías ferroviarias es la fuerza impulsora para el pandeo del riel. Este fenómeno resultó en 190 descarrilamientos de trenes durante 1998—2002 solamente en Estados Unidos.

    Expansión térmica: Una breve introducción a la expansión térmica para estudiantes.

    Expansión, no contracción

    ¿Por qué la materia suele expandirse cuando se calienta? La respuesta se puede encontrar en la forma del típico potencial partícula-partícula en la materia. Las partículas en sólidos y líquidos sienten constantemente la presencia de otras partículas vecinas. Esta interacción se puede representar matemáticamente como una curva de potencial. La figura 2 ilustra cómo este potencial entre partículas suele tomar una forma asimétrica en lugar de una forma simétrica, en función de la distancia partícula-partícula. Tenga en cuenta que la curva de potencial es más pronunciada para una distancia más corta. En el diagrama, (b) muestra que a medida que la sustancia se calienta, aumenta la distancia de equilibrio (o promedio) partícula-partícula. Los materiales que se contraen o mantienen su forma al aumentar la temperatura son raros. Este efecto es limitado en tamaño, y solo ocurre dentro de rangos de temperatura limitados.

    imagen

    Fig 2: Potencial interpartícula típico en materia condensada (tal como sólida o líquida).

    Expansión Lineal

    A una primera aproximación, el cambio en las mediciones de longitud de un objeto (dimensión lineal a diferencia de, por ejemplo, dimensión volumétrica) debido a la expansión térmica está relacionado con el cambio de temperatura por un coeficiente de expansión lineal. Es el cambio fraccionario de longitud por grado de cambio de temperatura. Asumiendo un efecto insignificante de la presión, podemos escribir:

    \[\mathrm{α_L=\dfrac{1}{L}\dfrac{dL}{dT},}\]

    donde\(\mathrm{L}\) es una medida de longitud particular y\(\mathrm{\frac{dL}{dT}}\) es la tasa de cambio de esa dimensión lineal por unidad de cambio de temperatura. A partir de la definición del coeficiente de expansión, se\(\mathrm{ΔT}\) puede estimar que el cambio en la dimensión\(\mathrm{ΔL}\) lineal en un rango de temperatura es:

    \[\mathrm{\dfrac{ΔL}{L}=α_LΔT.}\]

    Esta ecuación funciona bien siempre y cuando el coeficiente de expansión lineal no cambie mucho sobre el cambio de temperatura. Si lo hace, la ecuación debe estar integrada.

    Expansión de área

    Los objetos se expanden en todas las dimensiones. Es decir, sus áreas y volúmenes, así como sus longitudes, aumentan con la temperatura.

    objetivos de aprendizaje

    • Expresar el coeficiente de expansión térmica del área en forma de ecuación

    Aprendimos sobre la expansión lineal (en una dimensión) en el Átomo anterior. Los objetos se expanden en todas las dimensiones, y podemos extender la expansión térmica para 1D a dos (o tres) dimensiones. Es decir, sus áreas y volúmenes, así como sus longitudes, aumentan con la temperatura.

    Quiz

    Antes de indagar en detalles, aquí hay una pregunta interesante. Imagina que tenemos una lámina rectangular de metal con un agujero circular en el medio. Si se calienta el metal, podemos adivinar que la pieza, en general, se hará más grande debido a la expansión térmica. Ahora bien, ¿qué va a pasar con el agujero circular en el medio? ¿El agujero va a ser más grande o más pequeño? Respuesta: Imagínese que tenemos una lámina metálica similar pero sin agujero. Dibuja una línea circular imaginaria que representa el agujero circular en nuestro cuestionario. ¿Cómo cambia este círculo imaginario a medida que se calienta el metal? Sí. Se hará más grande. Por lo tanto, puedes adivinar que el agujero en nuestro quiz se hará más grande.

    imagen

    Fig 1: En general, los objetos se expanden en todas las direcciones a medida que aumenta la temperatura. En estos dibujos, los límites originales de los objetos se muestran con líneas continuas, y los límites expandidos con líneas discontinuas. a) El área aumenta debido a que aumentan tanto la longitud como la anchura. El área de un tapón circular también aumenta. (b) Si se quita el tapón, el orificio que deja se hace más grande con el aumento de la temperatura, tal como si el tapón expandible estuviera todavía en su lugar.

    Coeficiente de expansión térmica de área

    El coeficiente de expansión térmica del área relaciona el cambio en las dimensiones del área de un material con un cambio en la temperatura. Es el cambio fraccionario de área por grado de cambio de temperatura. Haciendo caso omiso de la presión, podemos escribir:\(\mathrm{α_A=\dfrac{1}{A}\dfrac{dA}{dT}}\), donde hay alguna área de interés sobre el objeto, y\(\mathrm{\frac{dA}{dT}}\) es la tasa de cambio de esa área por unidad de cambio de temperatura. El cambio en la dimensión lineal se puede estimar como:\(\mathrm{\frac{ΔA}{A}=α_AΔT}\). Esta ecuación funciona bien siempre y cuando el coeficiente de expansión lineal no cambie mucho sobre el cambio de temperatura\(\mathrm{ΔT}\). Si lo hace, la ecuación debe estar integrada.

    Relación con el coeficiente de expansión térmica lineal

    Para materiales isotrópicos, y para pequeñas expansiones, el coeficiente de expansión térmica lineal es la mitad del coeficiente de área. Para derivar la relación, tomemos un cuadrado de acero que tenga lados de longitud L. El área original será\(\mathrm{A = L^2}\), y la nueva área, después de un aumento de temperatura, será

    \[\begin{align} \mathrm{A+ΔA} & \mathrm{=(L+ΔL)^2} \\ & \mathrm{=L^2+2LΔL+(ΔL)^2} \\ & \mathrm{≈L^2+2LΔL} \\ & \mathrm{=A+2A\dfrac{ΔL}{L}} \end{align} \]

    La aproximación se mantiene para una\(\mathrm{ΔL}\) cámara suficientemente pequeña a\(\mathrm{L}\). Ya que\(\mathrm{\dfrac{ΔA}{A}=2\dfrac{ΔL}{L}}\) a partir de la ecuación anterior (y de las definiciones de los coeficientes térmicos), obtenemos\(\mathrm{α_A=2_{αL}}\).

    Expansión de Volumen

    Las sustancias se expanden o contraen cuando su temperatura cambia, con expansión o contracción ocurriendo en todas las direcciones.

    objetivos de aprendizaje

    • Comparar los efectos de la presión sobre la expansión de materiales gaseosos y sólidos

    El coeficiente de expansión térmica volumétrica es el coeficiente de expansión térmica más básico. ilustra que, en general, las sustancias se expanden o contraen cuando su temperatura cambia, con expansión o contracción ocurriendo en todas las direcciones. Tales sustancias que se expanden en todas las direcciones se llaman isotrópicas. Para los materiales isotrópicos, el área y los coeficientes lineales pueden calcularse a partir del coeficiente volumétrico (discutido a continuación).

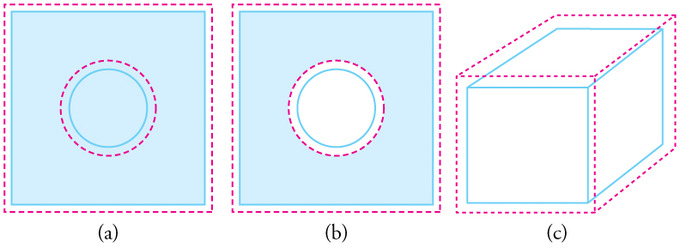
    imagen

    Expansión volumétrica: En general, los objetos se expanden en todas direcciones a medida que aumenta la temperatura En estos dibujos, los límites originales de los objetos se muestran con líneas continuas, y los límites expandidos con líneas discontinuas. a) El área aumenta debido a que aumentan tanto la longitud como la anchura. El área de un tapón circular también aumenta. (b) Si se quita el tapón, el orificio que deja se hace más grande con el aumento de la temperatura, tal como si el tapón expandible estuviera todavía en su lugar. (c) El volumen también aumenta, porque las tres dimensiones aumentan.

    Expansión Térmica — Expansión de Volumen: Una breve introducción a la expansión térmica para estudiantes.

    Las definiciones matemáticas de estos coeficientes se definen a continuación para sólidos, líquidos y gases:

    \[\mathrm{α_V=\dfrac{1}{V}(\dfrac{∂V}{∂T})p.}\]

    El subíndice p indica que la presión se mantiene constante durante la expansión. En el caso de un gas, es importante que la presión se mantenga constante, ya que el volumen de un gas variará apreciablemente con la presión así como con la temperatura.

    Para un sólido, podemos ignorar los efectos de la presión sobre el material, así se puede escribir el coeficiente de expansión térmica volumétrica:

    \[\mathrm{α_V=\dfrac{1}{V}\dfrac{dV}{dT},}\]

    donde V es el volumen del material, y es dV/dt la tasa de cambio de ese volumen con la temperatura. Esto significa que el volumen de un material cambia en alguna cantidad fraccionaria fija. Por ejemplo, un bloque de acero con un volumen de 1 metro cúbico podría expandirse a 1.002 metros cúbicos cuando la temperatura se eleva 50 °C, es decir, una expansión de 0.2%. El coeficiente de expansión volumétrica sería de 0.2% para 50 °C, o 0.004% por grado C.

    Relación con el coeficiente de expansión térmica lineal

    Para el material isotrópico, y para pequeñas expansiones, el coeficiente de expansión térmica lineal es un tercio del coeficiente volumétrico. Para derivar la relación, tomemos un cubo de acero que tenga lados de longitud L. El volumen original será\(\mathrm{V = L^3}\), y el nuevo volumen, después de un aumento de temperatura, será:

    \[\begin{align} \mathrm{V+ΔV} & \mathrm{=(L+ΔL)^3} \\ & \mathrm{=L^3+3L^2ΔL+3L(ΔL)^2+(ΔL)^3} \\ & \mathrm{≈L^3+3L^2ΔL} \\ & \mathrm{=V+3V\dfrac{ΔL}{L}.} \end{align}\]

    La aproximación se mantiene para una suficientemente pequeña\(\mathrm{ΔL}\) en comparación con L. Desde:

    \[\mathrm{\dfrac{ΔV}{V}=3\dfrac{ΔL}{L}}\]

    (y de las definiciones de los coeficientes térmicos), llegamos a:

    \[\mathrm{α_V=3α_L}\]

    Propiedades Especiales del Agua

    Los objetos se expandirán con el aumento de la temperatura, pero el agua es la excepción más importante a la regla general.

    objetivos de aprendizaje

    • Describir las propiedades de expansión térmica del agua

    Propiedades Especiales del Agua

    En general, los objetos se expandirán con el aumento de la temperatura. Sin embargo, una serie de materiales se contraen al calentar dentro de ciertos rangos de temperatura; esto generalmente se llama expansión térmica negativa, en lugar de “contracción térmica”. El agua es la excepción más importante a la regla general. El agua tiene esta característica única debido a la naturaleza particular del enlace de hidrógeno en H 2 O.

    Densidad del agua a medida que cambia la temperatura

    A temperaturas mayores a 4ºC (40ºF) el agua se expande al aumentar la temperatura (su densidad disminuye). Sin embargo, se expande con la disminución de la temperatura cuando está entre +4ºC y 0ºC (40ºF a 32ºF). El agua es más densa a +4ºC.

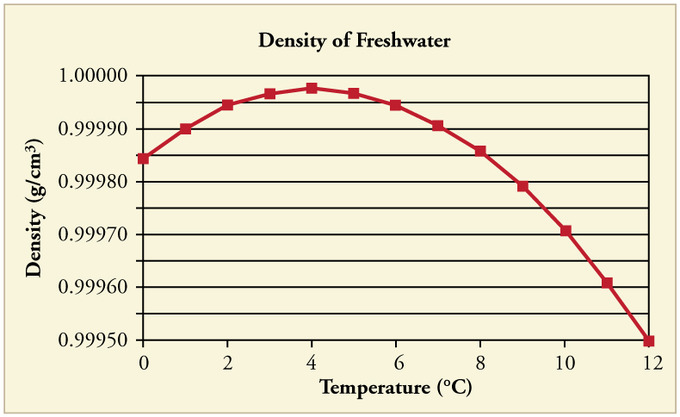
    imagen

    Densidad del agua vs. Temperatura: La densidad del agua en función de la temperatura. Tenga en cuenta que la expansión térmica es en realidad muy pequeña. La densidad máxima a +4ºC es solo 0.0075% mayor que la densidad a 2ºC, y 0.012% mayor que la de 0ºC.

    Quizás el efecto más llamativo de este fenómeno es la congelación del agua en un estanque. Cuando el agua cerca de la superficie se enfría hasta 4ºC es más densa que el agua restante y así se hundirá hasta el fondo. Esta “rotación” da como resultado una capa de agua más cálida cerca de la superficie, que luego se enfría. Eventualmente el estanque tiene una temperatura uniforme de 4ºC. Si la temperatura en la capa superficial cae por debajo de los 4ºC, el agua es menos densa que el agua de abajo, y así permanece cerca de la parte superior.

    Como resultado, la superficie del estanque puede congelarse completamente, mientras que el fondo puede permanecer a 4ºC. El hielo en la parte superior del agua líquida proporciona una capa aislante de las duras temperaturas del aire exterior del invierno. Los peces y otras especies acuáticas pueden sobrevivir en agua a 4ºC bajo el hielo, debido a esta característica inusual del agua. También produce circulación de agua en el estanque que es necesaria para un ecosistema saludable del cuerpo de agua.

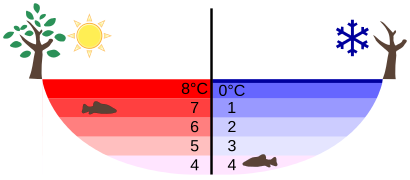
    imagen

    Temperatura en un lago: Distribución de la temperatura en un lago en días cálidos y fríos en invierno

    Hielo Versus Agua

    La forma sólida de la mayoría de las sustancias es más densa que la fase líquida; así, un bloque de la mayoría de los sólidos se hundirá en el líquido. Sin embargo, un bloque de hielo flota en agua líquida porque el hielo es menos denso. Al congelarse, la densidad del agua disminuye aproximadamente 9%.

    Puntos Clave

    • El potencial entre partículas generalmente toma una forma asimétrica, en lugar de una forma simétrica en función de la distancia partícula-partícula. Por ello, la materia se expande y se contrae a medida que cambia la temperatura
    • El cambio en las mediciones de longitud de un objeto debido a la expansión térmica está relacionado con el cambio de temperatura por un “coeficiente de expansión lineal”, que se da como\(\mathrm{α_L=\dfrac{1}{L} \dfrac{dL}{dT}}\).
    • El coeficiente de expansión lineal es solo como una aproximación a lo largo de un intervalo de temperatura estrecho.
    • El coeficiente de expansión térmica del área relaciona el cambio en las dimensiones del área de un material con un cambio en la temperatura. Se define como\(\mathrm{α_A=\dfrac{1}{A}\dfrac{dA}{dT}}\).
    • La relación entre el área y el coeficiente de expansión térmica lineal se da de la siguiente manera:\(\mathrm{α_A=2α_L}\).
    • Al igual que el coeficiente de expansión lineal, el coeficiente de expansión térmica de área funciona como una aproximación solo a lo largo de un intervalo de temperatura estrecho.
    • Las sustancias que se expanden a la misma velocidad en todas las direcciones se denominan isotrópicas.
    • En el caso de un gas, la expansión depende de cómo cambió la presión en el proceso debido a que el volumen de un gas variará apreciablemente con la presión y la temperatura.
    • Para un sólido, podemos ignorar los efectos de la presión sobre el material, y el coeficiente de expansión térmica volumétrica se puede escribir como\(\mathrm{α_V=\dfrac{1}{V}\dfrac{dV}{dT}}\). Para materiales isotrópicos,\(\mathrm{α_V=3α_L}\).
    • El agua se expande al aumentar la temperatura (su densidad disminuye) cuando se encuentra a temperaturas superiores a 4ºC (40ºF). Sin embargo, se expande con la disminución de la temperatura cuando está entre +4ºC y 0ºC (40ºF a 32ºF). El agua es más densa a +4ºC.
    • Debido a la peculiar propiedad de expansión térmica del agua, la superficie de un estanque puede congelarse completamente, mientras que el fondo puede permanecer a 4ºC. Los peces y otras especies acuáticas pueden sobrevivir en agua a 4ºC bajo el hielo, debido a esta característica inusual del agua.
    • La forma sólida de la mayoría de las sustancias es más densa que la fase líquida; así, un bloque de la mayoría de los sólidos se hundirá en el líquido. Sin embargo, un bloque de hielo flota en agua líquida porque el hielo es menos denso.

    Términos Clave

    • potencial: Una curva que describe la situación en la que la diferencia en las energías potenciales de un objeto en dos posiciones diferentes depende únicamente de esas posiciones.
    • coeficiente de expansión térmica lineal: El cambio fraccionario de longitud por grado de cambio de temperatura.
    • isotrópico: Tener propiedades idénticas en todas las direcciones; exhibir isotropía.
    • enlace de hidrógeno: Un enlace débil en el que un átomo de hidrógeno en una molécula es atraído por un átomo electronegativo (generalmente nitrógeno u oxígeno) en la misma o diferente molécula.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 12.3: Expansión Térmica is shared under a not declared license and was authored, remixed, and/or curated by Boundless.