Saltar al contenido principal
LibreTexts Español

15.1: Introducción

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128125
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Ondas mecánicas y electromagnéticas de contraste

    Visión general

    Una onda es una oscilación que viaja por el espacio, acompañada de una transferencia de energía. El movimiento de las olas transfiere energía de un punto a otro, a menudo sin desplazamiento permanente de las partículas del medio, es decir, con poco o ningún transporte masivo asociado. Consisten, en cambio, en oscilaciones o vibraciones alrededor de ubicaciones casi fijas. Hay dos tipos principales de olas. Las ondas mecánicas se propagan a través de un medio, y la sustancia de este medio se deforma. La deformación se invierte por sí misma debido a las fuerzas restauradoras resultantes de su deformación.

    El segundo tipo principal de onda, las ondas electromagnéticas, no requieren un medio (aunque aún pueden propagarse a través de un medio). En cambio, consisten en oscilaciones periódicas en campos eléctricos y magnéticos generados por partículas cargadas, y por lo tanto pueden viajar a través de un vacío.

    Ecuación de Onda

    La forma de una onda puede tomar la forma de cualquier función que se repita sobre alguna escala espacial característica λλ, la longitud de onda (ver). Más generalmente, las formas de onda son funciones escalares uu que satisfacen la ecuación de onda,\(\mathrm{\frac{∂^2u}{∂t^2}=c^2∇^2u}\). Esta ecuación simplemente establece que la aceleración de la forma de onda (Izquierda: segunda derivada con respecto al tiempo) es proporcional a la Laplaciana (Derecha: segunda derivada espacial) de la misma forma de onda. La constante de proporcionalidad,\(\mathrm{c^2}\), es el cuadrado de la velocidad de propagación de la onda.

    imagen

    Formas de onda comunes: Una muestra de varias formas de onda comunes y simples. Una forma de onda es una función que se repite en el espacio.

    Onda sinusoidal

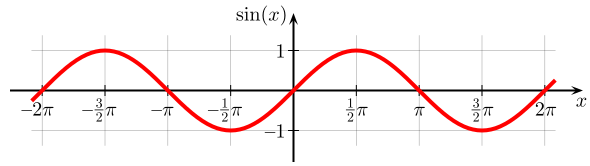
    imagen

    Trama de seno: La función sinusoidal graficada en el plano cartesiano. En esta gráfica, el ángulo x se da en radianes (π = 180°).

    Considera una de las formas de onda más comunes, la sinusoide. Una forma general de onda sinusoidal es\(\mathrm{y(x,t)=A \sin (kx−ωt+ϕ)}\), donde A es la amplitud de la onda,\(\mathrm{ω}\) es la frecuencia angular de la onda, k es el número de onda y\(\mathrm{ϕ}\) es la fase de la onda sinusoidal dada en radianes. Esta forma de onda da la posición de desplazamiento (“y”) de una partícula en un medio desde su equilibrio en función tanto de la posición “x” como del tiempo “t”.

    Al tomar derivadas, es evidente que la ecuación de onda dada anteriormente se mantiene para\(\mathrm{c=\frac{ω}{k}}\), lo que también se llama la velocidad de fase de la onda. Para encontrar la velocidad de una partícula en el medio a x y t, tomamos la derivada temporal de la forma de onda para obtener\(\mathrm{∂y(x,t)∂t=−Aω \cos (kx−ωt+ϕ)}\). De igual manera, para encontrar la aceleración de la partícula desplazada en el medio a x y t, tomamos la segunda derivada para obtener\(\mathrm{\frac{∂^2y(x,t)}{∂t^2}=−Aω^2 \sin (kx−ωt+ϕ)}\). Obsérvese la relación de fase entre las funciones trigonométricas en\(\mathrm{y(x,t), y'(x,t), y”(x,t)}\). Cuando el desplazamiento de partículas es máximo o mínimo, la velocidad es 0. Cuando el desplazamiento es 0, la velocidad de las partículas es máxima o mínima. De igual manera, la aceleración de partículas es máxima (o mínima) cuando el desplazamiento de la partícula es mínimo (o máximo), respectivamente.

    Onda Arbitraria

    Observamos de cerca la onda sinusoidal. Pero, ¿qué tal olas que tienen una forma general? Un aspecto importante de la ecuación de onda es su linealidad: la ecuación de onda es lineal en u y se deja inalterada por las traducciones en el espacio y el tiempo. Dado que una onda con una forma arbitraria puede ser representada por una suma de muchas ondas sinusoidales (esto se llama análisis de Fourier), podemos generar una gran variedad de soluciones de la ecuación de onda traduciendo y sumando ondas sinusoidales que acabamos de observar de cerca.

    Puntos Clave

    • La ecuación de onda requiere que la segunda derivada temporal de la forma de onda sea proporcional a su segunda derivada espacial.
    • Las formas de onda describen la forma de las ondas físicas, y pueden tomar la forma de cualquier función que se repita en el espacio.
    • Una de las formas de onda más comunes en la física es la sinusoide. Dado que cualquier forma de onda de arbitraje se puede generar agregando un conjunto de ondas sinusoidales, la física que gobierna una onda de forma arbitraria puede describirse usando sus componentes de onda sinusoidal.

    Términos Clave

    • forma de onda: La forma de una onda física, como el sonido o la radiación electromagnética. La forma puede ser cualquier función que se repita en el espacio.
    • Análisis de Fourier: Estudio de la manera en que las funciones generales pueden ser representadas o aproximadas por sumas de funciones trigonométricas más simples.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 15.1: Introducción is shared under a not declared license and was authored, remixed, and/or curated by Boundless.