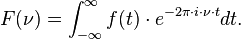32.10: Análisis de Fourier

Última actualización
Guardar como PDF

Page ID: 79690

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La transformada de Fourier convierte una función vs. tiempo continuo (o descretado) y la mapea en una función vs. frecuencias continuas (o descretadas). Por lo tanto, la transformada convierte datos de dominio de tiempo en datos de dominio de frecuencia (y viceversa). Esta descomposición de una función en sinusoides de diferentes frecuencias es un enfoque poderoso para muchos problemas experimentales y teóricos. La espectroscopia por transformada de Fourier es un enfoque mediante el cual los espectros se recopilan en base a mediciones que utilizan mediciones en el dominio del tiempo o del espacio de la radiación electromagnética u otro tipo de radiación. Se puede aplicar a una variedad de tipos de espectroscopía incluyendo espectroscopia óptica, espectroscopia infrarroja (FT IR, FT-NIRS), resonancia magnética nuclear de transformada de Fourier (RMN), espectrometría de masas y espectroscopia de resonancia de espín electrónico.

Introducción

El análisis de Fourier es un área temática que surgió del estudio de las series de Fourier. El sujeto comenzó tratando de entender cuándo era posible representar funciones generales mediante sumas de funciones trigonométricas más simples. El intento de entender funciones (u otros objetos) dividiéndolas en piezas básicas que son más fáciles de entender es uno de los temas centrales en el análisis de Fourier. El análisis de Fourier lleva el nombre de Joseph Fourier quien demostró que representar una función mediante una serie trigonométrica simplificó enormemente el estudio de la propagación del calor. Hoy en día el tema del análisis de Fourier abarca un vasto espectro de matemáticas con partes que, a primera vista, pueden parecer bastante diferentes. En las ciencias y la ingeniería el proceso de descomponer una función en piezas más simples se suele llamar análisis. En el análisis de Fourier, el término transformada de Fourier a menudo se refiere al proceso que descompone una función dada en las piezas básicas. Este proceso da como resultado otra función que describe cuánto de cada pieza básica hay en la función original. Sin embargo, a la transformación se le suele dar un nombre más específico dependiendo del dominio y otras propiedades de la función que se está transformando, como se detalla a continuación. Además, el concepto original del análisis de Fourier se ha extendido a lo largo del tiempo para aplicarlo a situaciones cada vez más abstractas y generales, y el campo general a menudo se conoce como análisis armónico.

Serie de Fourier

Cuando la función ¡es una función del tiempo y representa una señal física, la transformada tiene una interpretación estándar como el espectro de frecuencia de la señal. La magnitud de la función F de valor complejo resultante a la frecuencia ω representa la amplitud de un componente de frecuencia cuya fase inicial viene dada por la fase de F. Sin embargo, es importante darse cuenta de que las transformadas de Fourier no se limitan a funciones de tiempo y frecuencias temporales. Se pueden aplicar igualmente para analizar frecuencias espaciales, y de hecho para casi cualquier dominio de función.

Propiedades

http://www.math.ubc.ca/~feldman/demos/demo3.html

Transnform continuo de Fourier (CFT)

Muy a menudo, el término no calificado transformada de Fourier se refiere a la transformación de funciones de un argumento real continuo, como el tiempo (t). En este caso la transformada de Fourier describe una función ¡(t) en términos de exponenciales complejos básicos de diversas frecuencias. En términos de frecuencia ordinaria ν, la transformada de Fourier viene dada por el número complejo:

$F (\ nu) =\ int_ {-\ infty} ^ {\ infty} f (t)\ cdot e^ {- 2\ pi\ cdot i\ cdot\ cdot\ nu\ cdot t} dt.$

Evaluar esta cantidad para todos los valores de ν produce la función de dominio de frecuencia.

Transformada Discreta de Fourier (DFT)

Experimentalmente, recolectamos datos que no son continuos, sino que se toman muestras de mediciones en un punto específico. De ahí que tengamos que lidiar con la versión discreta de la Transformada de Fourier.

Transferencia rápida de Fourier (FFT)

La versión discreta de la transformada de Fourier (ver abajo) se puede evaluar rápidamente en computadoras usando algoritmos de transformada rápida de Fourier (FFT). Este algortihm requiere de manera sintomática un número de 2 ⁿ de mediciones para operar. De ahí que notará conjuntos de datos a menudo con tales dimensiones. (Conte & de Boor 1980)

Referencias

Arfken, G. “Serie de Fourier”. Ch. 14 en Métodos Matemáticos para Físicos, 3a ed. Orlando, FL: Academic Press, pp. 760-793, 1985.
Askey, R. y Haquimo, D. T. “Similitudes entre Fourier y Power Series”. Amer. Matemáticas. Mensual 103, 297-304, 1996.
Beyer, W. H. (Ed.). Tablas Matemáticas Estándar CRC, 28a ed. Boca Raton, FL: CRC Press, 1987.
Brown, J. W. y Churchill, R. V. Serie de Fourier y Problemas de Valor Límite, 5a ed. Nueva York: McGraw-Hill, 1993.
Byerly, W. E. Un tratado elemental sobre series de Fourier, y armónicos esféricos, cilíndricos y elipsoidales, con aplicaciones a problemas en física matemática. Nueva York: Dover, 1959.
Carslaw, H. S. Introducción a la Teoría de las Series e Integrales de Fourier, 3a ed., rev. y enl. Nueva York: Dover, 1950.
Davis, H. F. Serie de Fourier y Funciones Ortogonales. Nueva York: Dover, 1963.
Dym, H. y McKean, H. P. Serie de Fourier e Integrales. Nueva York: Academic Press, 1972.
Folland, G. B. Análisis de Fourier y sus aplicaciones. Pacific Grove, CA: Brooks/Cole, 1992.
Groemer, H. Aplicaciones Geométricas de la Serie de Fourier y Armónicos Esféricos. Nueva York: Cambridge University Press, 1996.
Körner, T. W. Análisis de Fourier. Cambridge, Inglaterra: Cambridge University Press, 1988.
Körner, T. W. Ejercicios para Análisis de Fourier. Nueva York: Cambridge University Press, 1993.
Krantz, S. G. “Serie de Fourier”. §15.1 en Manual de Variables Complejas. Boston, MA: Birkhäuser, pp. 195-202, 1999.
Lighthill, M. J. Introducción al Análisis de Fourier y Funciones Generalizadas. Cambridge, Inglaterra: Cambridge University Press, 1958.
Morrison, N. Introducción al Análisis de Fourier. Nueva York: Wiley, 1994.
Sansone, G. “Expansiones en la Serie de Fourier”. Ch. 2 en Funciones ortogonales, rev. English ed. Nueva York: Dover, pp. 39-168, 1991.
Weisstein, E. W. “Libros sobre Transformadas de Fourier”. http://www.ericweisstein.com/encyclopedias/books/FourierTransforms.html.
Whittaker, E. T. y Robinson, G. “Análisis Práctico de Fourier”. Capítulo 10 en El cálculo de las observaciones: un tratado de matemáticas numéricas, 4ª ed. Nueva York: Dover, pp. 260-284, 1967.
Espectroscopia de R. R. Williams y la Transformada de Fourier Wiley: Nueva York, 1995
Bettis, Acantilado; Lyons, Edward J.; Brooks, David W. J. Chem. Educ. 1996, 73, 839
Graff, Daria K. J. Chem. Educ. 1995, 72, 304.
Chesick, John P. J. Chem. Educ. 1989, 66, 128.
Glasser, L. J. Chem. Educ. 1987, 64, A228.
Glasser, L. J.Chem. Educ. 1987, 64, A255.
Glasser, L. J. Chem. Educ. 1987, 64, A306.

Colaboradores y Atribuciones

Entrada de Wikipedia (para empezar)
MMRC.Caltech.edu/FTIR/FTIRIntro.pdf