15.5: Olas

objetivos de aprendizaje

• Describir proceso de energía y transferencia de masa durante el movimiento de las olas

Las vibraciones y las ondas son fenómenos extremadamente importantes en la física. En la naturaleza, las oscilaciones se encuentran en todas partes. Desde el movimiento de los átomos hasta las grandes oscilaciones de las olas del mar, encontramos ejemplos de vibraciones en casi todos los sistemas físicos. En física una onda puede pensarse como una perturbación u oscilación que viaja a través del espacio-tiempo, acompañada de una transferencia de energía. El movimiento de las olas transfiere energía de un punto a otro, a menudo sin desplazamiento permanente de las partículas del medio, es decir, con poco o ningún transporte masivo asociado. Consisten, en cambio, en oscilaciones o vibraciones alrededor de ubicaciones casi fijas.

El énfasis del último punto resalta un importante concepto erróneo de las olas. Las olas transfieren energía, no masa. Una manera fácil de ver esto es imaginar una pelota flotante a unos metros del mar. A medida que las olas se propagan (es decir, viajan) hacia la orilla, la pelota no llegará hacia la orilla. Puede llegar a la orilla eventualmente debido a las mareas, la corriente o el viento, pero las olas mismas no llevarán la pelota con ellas. Una ola solo mueve la masa perpendicular a la dirección de propagación, en este caso hacia arriba y hacia abajo, como se ilustra en la siguiente figura:

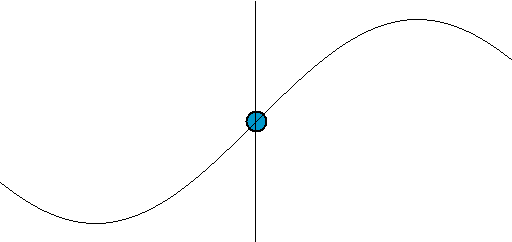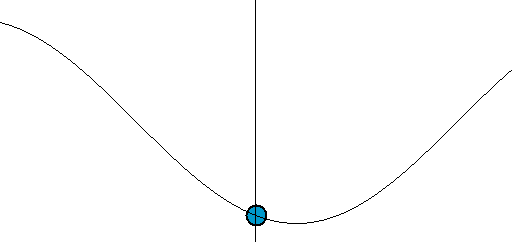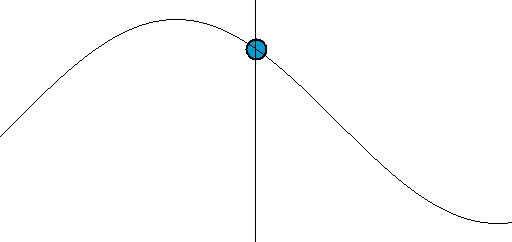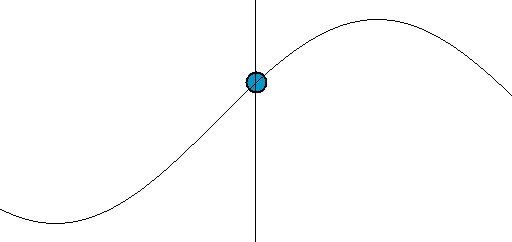
Movimiento de las olas: El punto a lo largo del eje es análogo a la bola flotante en el mar. Notamos que mientras se mueve hacia arriba y hacia abajo no se mueve en la dirección de la propagación de la onda.

Una onda puede ser transversal o longitudinal dependiendo de la dirección de su oscilación. Las ondas transversales ocurren cuando una perturbación provoca oscilaciones perpendiculares (en ángulo recto) a la propagación (la dirección de transferencia de energía). Las ondas longitudinales ocurren cuando las oscilaciones son paralelas a la dirección de propagación. Si bien las ondas mecánicas pueden ser tanto transversales como longitudinales, todas las ondas electromagnéticas son transversales. El sonido, por ejemplo, es una onda longitudinal.

La descripción de las ondas está estrechamente relacionada con su origen físico para cada instancia específica de un proceso de onda. Por ejemplo, la acústica se distingue de la óptica en que las ondas sonoras están relacionadas con una transferencia de ondas mecánicas más que electromagnéticas (de luz) causadas por la vibración. Por lo tanto, conceptos como masa, impulso, inercia o elasticidad se vuelven cruciales para describir los procesos de onda acústica (a diferencia de la óptica). Esta diferencia de origen introduce ciertas características de onda particulares a las propiedades del medio involucrado. En este capítulo examinaremos de cerca la diferencia entre ondas longitudinales y transversales junto con algunas de las propiedades que poseen. También aprenderemos cómo las ondas son fundamentales para describir el movimiento de muchos sistemas físicos aplicables.

La ecuación de onda: una breve introducción a la ecuación de onda, discutiendo la velocidad de onda, frecuencia, longitud de onda y período de onda.

Ondas Transversales

Las ondas transversales se propagan a través de medios con una velocidad →vwv→w ortogonalmente a la dirección de transferencia de energía.

objetivos de aprendizaje

• Describir las propiedades de la onda transversal

Una onda transversal es una onda móvil que consiste en oscilaciones que ocurren perpendiculares (o en ángulo recto) a la dirección de transferencia de energía. Si una onda transversal se mueve en la dirección x positiva, sus oscilaciones están en direcciones hacia arriba y hacia abajo que se encuentran en el plano y—z. La luz es un ejemplo de onda transversal. Para las ondas transversales en materia, el desplazamiento del medio es perpendicular a la dirección de propagación de la onda. Una ondulación en un estanque y una ola en una cuerda son ondas transversales fácilmente visualizadas.

Las ondas transversales son ondas que oscilan perpendicularmente a la dirección de propagación. Si anclas un extremo de una cinta o cuerda y sostienes el otro extremo en tu mano, puedes crear ondas transversales moviendo tu mano hacia arriba y hacia abajo. Sin embargo, observe que también puede lanzar olas moviendo su mano de lado a lado. Este es un punto importante. Hay dos direcciones independientes en las que puede ocurrir el movimiento de las olas. En este caso, estas son las direcciones y y z mencionadas anteriormente. Representa el movimiento de una onda transversal. Aquí observamos que la onda se mueve en t y oscila en el plano x-y. Se puede pensar que una onda comprende muchas partículas (como se ve en la figura) que oscilan hacia arriba y hacia abajo. En la figura observamos que este movimiento está en el plano x-y (denotado por la línea roja en la figura). A medida que pasa el tiempo, las oscilaciones están separadas por unidades de tiempo. El resultado de esta separación es la curva sinusoidal que esperamos cuando trazamos posición versus tiempo.

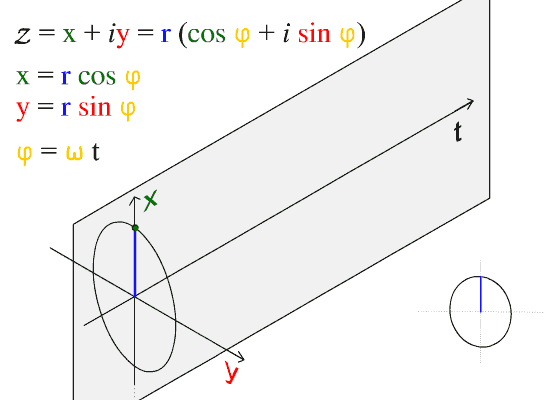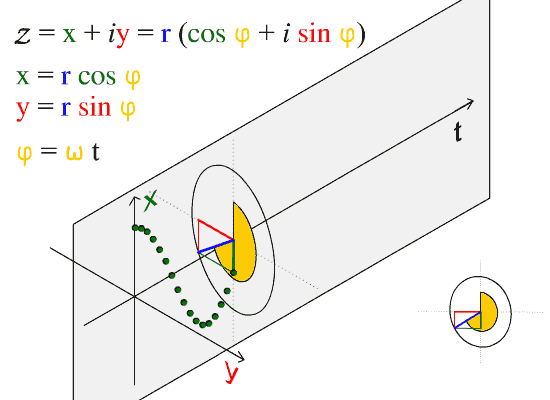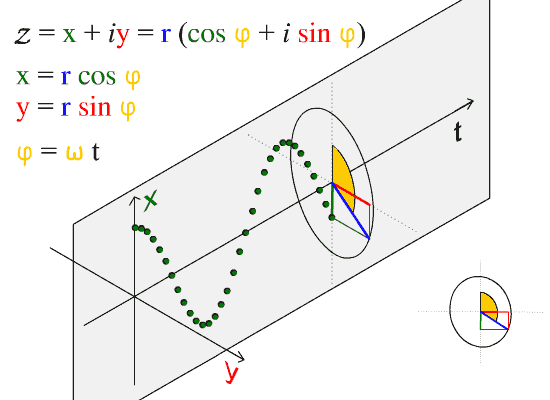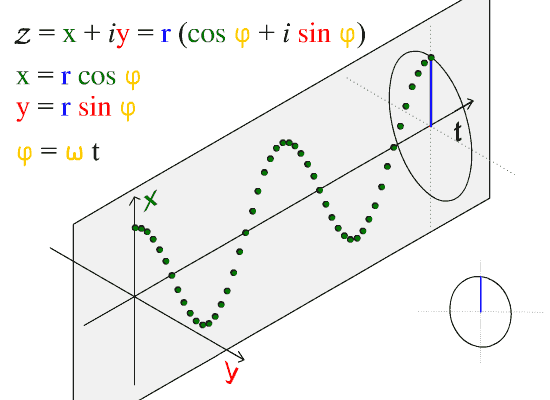
Onda sinusoidal: La dirección de propagación de esta onda es a lo largo del eje t.

Cuando una ola viaja a través de un medio, es decir, aire, agua, etc., o el medio de referencia estándar (vacío), lo hace a una velocidad dada: a esto se le llama velocidad de propagación. La velocidad a la que se propaga la onda se denota y se puede encontrar usando la siguiente fórmula:

\[\mathrm{v=fλ}\]

donde v es la velocidad de la onda, f es la frecuencia y es la longitud de onda. La longitud de onda abarca cresta a cresta mientras que la amplitud es 1/2 de la distancia total de cresta a canal. Las ondas transversales tienen sus aplicaciones en muchas áreas de la física. Ejemplos de ondas transversales incluyen ondas sísmicas S (secundarias), y el movimiento de los campos eléctrico (E) y magnético (M) en ondas planas electromagnéticas, las cuales oscilan perpendicularmente entre sí, así como a la dirección de transferencia de energía. Por lo tanto, una onda electromagnética consiste en dos ondas transversales, siendo la luz visible un ejemplo de una onda electromagnética.

Longitud de onda y amplitud: La longitud de onda es la distancia entre crestas adyacentes. La amplitud es el 1/2 la distancia de cresta a canal.

Dos Tipos de Olas: Longitudinal vs Transversal: ¡Incluso las olas del

Ondas longitudinales

Las ondas longitudinales, a veces llamadas ondas de compresión, oscilan en la dirección de propagación.

objetivos de aprendizaje

• Dar propiedades y proporcionar ejemplos de la onda longitudinal

Ondas longitudinales

Las ondas longitudinales tienen la misma dirección de vibración que su dirección de desplazamiento. Esto significa que el movimiento del medio está en la misma dirección que el movimiento de la ola. Algunas ondas longitudinales también se denominan ondas de compresión u ondas de compresión. Un experimento fácil para observar ondas longitudinales consiste en tomar un Slinky y sujetar ambos extremos. Después de comprimir y soltar un extremo del Slinky (mientras aún se mantiene en el extremo), un pulso de bobinas más concentradas viajará hasta el final del Slinky.

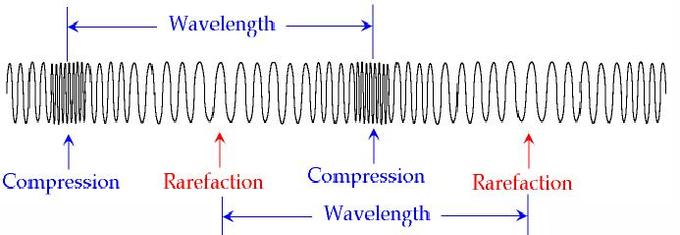
Ondas longitudinales: Un Slinky comprimido es un ejemplo de una onda longitudinal. El wve se propaga en la misma dirección de oscilación.

Al igual que las ondas transversales, las ondas longitudinales no desplazan la masa. La diferencia es que cada partícula que constituye el medio a través del cual se propaga una onda longitudinal oscila a lo largo del eje de propagación. En el ejemplo del Slinky, cada bobina oscilará en un punto pero no recorrerá la longitud del Slinky. Es importante recordar que la energía, en este caso en forma de pulso, se está transmitiendo y no la masa desplazada.

Las ondas longitudinales a veces también se pueden conceptualizar como ondas de presión. La onda de presión más común es la onda de sonido. Las ondas sonoras son creadas por la compresión de un medio, generalmente aire. Las ondas sonoras longitudinales son ondas de desviación de presión alterna de la presión de equilibrio, causando regiones locales de compresión y rarefacción. La materia en el medio es desplazada periódicamente por una onda sonora, y así oscila. Cuando las personas hacen un sonido, ya sea hablando o golpeando algo, están comprimiendo las partículas de aire en cierta cantidad significativa. Al hacerlo, crean ondas transversales. Cuando las personas escuchan sonidos, sus oídos son sensibles a las diferencias de presión e interpretan las ondas como diferentes tonos.

Dos Tipos de Olas: Longitudinal vs Transversal: ¡Incluso las olas del

Olas de Agua

Las olas de agua se pueden observar comúnmente en la vida diaria, y comprenden el movimiento de las olas tanto transversales como longitudinales.

objetivos de aprendizaje

• Describir el movimiento de partículas en olas de agua

Las olas de agua, que se pueden observar comúnmente en nuestra vida diaria, son de interés específico para los físicos. Describir la dinámica de fluidos detallada en las olas de agua está fuera del alcance de los cursos introductorios de física Aunque a menudo observamos la propagación de ondas de agua en 2D, en este átomo limitaremos nuestra discusión a la propagación 1D.

Ondas de agua: Olas superficiales en el agua

La singularidad de las olas de agua se encuentra en la observación de que comprenden tanto el movimiento de las olas transversales como longitudinales. Como resultado, las partículas que componen la onda se mueven en movimiento circular en sentido horario, como se ve en. El movimiento oscilatorio es mayor en la superficie y disminuye exponencialmente con la profundidad. Las olas son generadas por el viento que pasa sobre la superficie del mar. Siempre y cuando las olas se propaguen más lentamente que la velocidad del viento justo por encima de las olas, hay una transferencia de energía del viento a las olas. Tanto las diferencias de presión del aire entre el viento y el lado sotavento de la cresta de una ola, así como la fricción en la superficie del agua por el viento (haciendo que el agua entre en el esfuerzo cortante), contribuyen al crecimiento de las olas.

En el caso de las ondas planas lineales monocromáticas en aguas profundas, las partículas cercanas a la superficie se mueven en trayectorias circulares, creando una combinación de movimientos de onda longitudinales (ida y vuelta) y transversales (arriba y abajo). Cuando las ondas se propagan en aguas poco profundas (donde la profundidad es inferior a la mitad de la longitud de onda), las trayectorias de las partículas se comprimen en elipses A medida que aumenta la amplitud de onda (altura), las trayectorias de partículas ya no forman órbitas cerradas; más bien, después del paso de cada cresta, las partículas se desplazan ligeramente de sus posiciones anteriores, fenómeno conocido como deriva de Stokes.

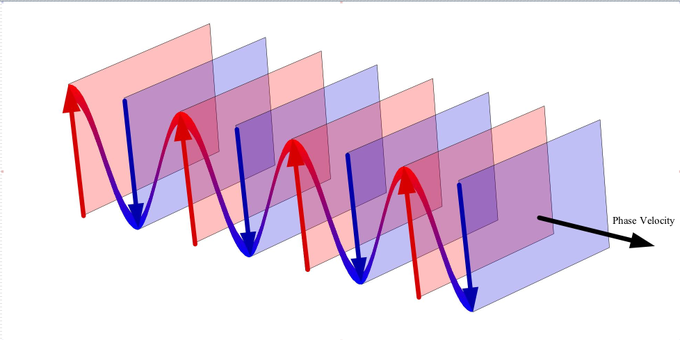
Onda plana: Vemos una onda propagándose en la dirección de la velocidad de fase. Se puede pensar que la onda está compuesta por planos ortogonales a la dirección de la velocidad de fase.

Desde que las olas de agua transportan energía, se han hecho intentos de generar energía a partir de ellas utilizando el movimiento físico de tales olas. Aunque las olas más grandes son más potentes, la potencia de las olas también está determinada por la velocidad de las olas, la longitud de onda y la densidad El agua profunda corresponde con una profundidad de agua mayor a la mitad de la longitud de onda, como es un caso común en el mar y el océano. En aguas profundas, las olas de período más largo se propagan más rápido y transportan su energía más rápido. La velocidad del grupo de aguas profundas es la mitad de la velocidad de fase. En aguas poco profundas para longitudes de onda mayores que aproximadamente veinte veces la profundidad del agua (como se encuentra a menudo cerca de la costa), la velocidad del grupo es igual a la velocidad de fase. Estos métodos han demostrado ser viables en algunos casos pero hasta la fecha no proporcionan una forma totalmente sustentable de energía renovable.

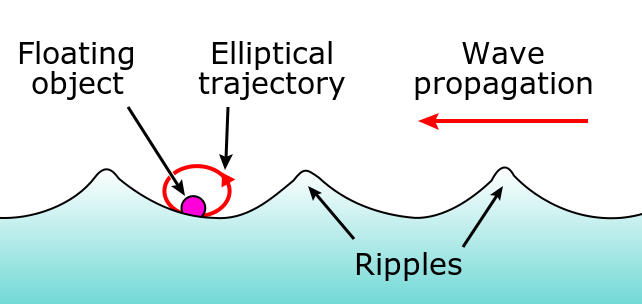
Ondas de agua: Las ondas de agua de movimiento hacen que las partículas sigan el movimiento circular en sentido horario Esto es resultado de que la onda tiene propiedades tanto transversales como longitudinales.

Longitud de onda, frecuencia en relación con la velocidad

Las ondas se definen por su frecuencia, longitud de onda y amplitud entre otras. También tienen dos tipos de velocidad: velocidad de fase y de grupo.

objetivos de aprendizaje

• Identificar las principales propiedades características de las olas

Características de Waves

Las olas tienen ciertas propiedades características que son observables a primera vista. La primera propiedad a tener en cuenta es la amplitud. La amplitud es la mitad de la distancia medida de cresta a canal. También observamos la longitud de onda, que es el período espacial de la onda (por ejemplo, de cresta a cresta o de valle a valle). Denotamos la longitud de onda por la letra griega λλ.

La frecuencia de una onda es el número de ciclos por unidad de tiempo; se puede pensar en ella como el número de crestas que pasan un punto fijo por unidad de tiempo. Matemáticamente, hacemos la observación de que,

Frecuencias de diferentes ondas sinusoidales. : La onda roja tiene un seno de baja frecuencia hay muy poca repetición de ciclos. Por el contrario decimos que la onda púrpura tiene una alta frecuencia. Observe que el tiempo aumenta a lo largo de la horizontal.

\[\mathrm{f=\dfrac{1}{T}}\]

donde T es el periodo de oscilación. La frecuencia y la longitud de onda también se pueden relacionar* con respecto a una “velocidad” de una onda. De hecho,

\ [\ mathrm {v=fλ}]

donde v se llama la velocidad de onda, o más comúnmente, la velocidad de fase, la velocidad a la que la fase de la onda se propaga en el espacio. Esta es la velocidad a la que viaja la fase de cualquier componente de frecuencia de la onda. Para tal componente, cualquier fase dada de la ola (por ejemplo, la cresta) parecerá viajar a la velocidad de fase.

Finalmente, la velocidad de grupo de una onda es la velocidad con la que la forma general de las amplitudes de las olas —conocida como modulación o envolvente de la onda— se propaga a través del espacio. En, uno puede ver que la forma general (o “envolvente”) se propaga hacia la derecha, mientras que la velocidad de fase es negativa.

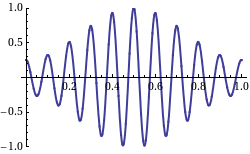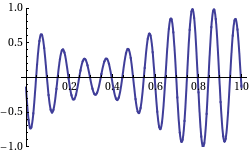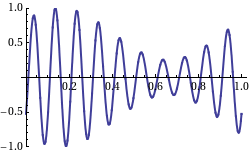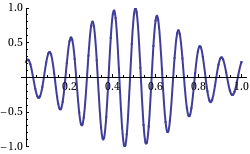
Fig 2: Esta muestra una onda con la velocidad de grupo y la velocidad de fase yendo en diferentes direcciones. (La velocidad del grupo es positiva y la velocidad de fase es negativa).

Transporte Energético

Las ondas transfieren energía que se puede utilizar para hacer el trabajo.

objetivos de aprendizaje

• Relacionar dirección de energía y transporte de olas

El transporte de energía es esencial para las olas. Es un error común pensar que las olas mueven masa. Las ondas transportan energía a lo largo de un eje definido como la dirección de propagación. Un ejemplo fácil es imaginar que estás parado en las olas y te golpea una ola significativamente grande, y una vez que te golpean te desplazas (¡a menos que te aferres firmemente a tu suelo!). En este sentido la ola ha hecho trabajo (aplicó una fuerza sobre una distancia). Dado que el trabajo se realiza a lo largo del tiempo, la energía transportada por una ola puede ser utilizada para generar energía.

Ola de Agua: Las olas que son más masivas o tienen una mayor velocidad transportan más energía.

De igual manera encontramos que las ondas electromagnéticas transportan energía. La radiación electromagnética (EMR) transporta energía, a veces llamada energía radiante, a través del espacio continuamente lejos de la fuente (esto no es cierto para la parte de campo cercano del campo EM). Las ondas electromagnéticas pueden imaginarse como una onda oscilante transversal autopropagante de campos eléctricos y magnéticos. EMR también lleva impulso y momento angular. Todas estas propiedades pueden impartirse a la materia con la que interactúa (a través del trabajo). La EMR se produce a partir de otros tipos de energía cuando se crea, y se convierte en otros tipos de energía cuando se destruye. El fotón es el cuántico de la interacción electromagnética, y es la “unidad” básica o constituyente de todas las formas de EMR. La naturaleza cuántica de la luz se vuelve más evidente a altas frecuencias (o alta energía fotónica). Dichos fotones se comportan más como partículas que los fotones de menor frecuencia.

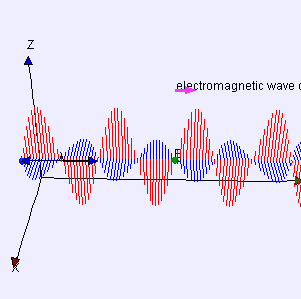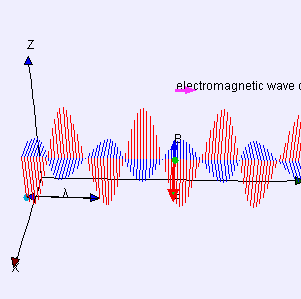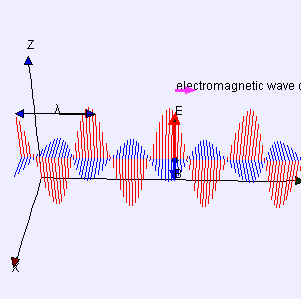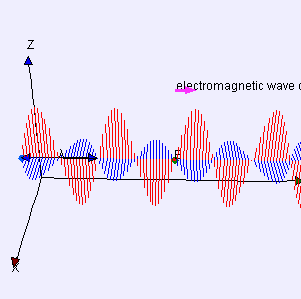
Onda electromagnética: Las ondas electromagnéticas pueden imaginarse como una onda oscilante transversal autopropagante de campos eléctricos y magnéticos. Este diagrama 3D muestra una onda polarizada linealmente plana que se propaga de izquierda a derecha.

En general, existe una relación de ondas que establece que la velocidad (\(\mathrm{v}\)) de una onda es proporcional a la frecuencia (\(\mathrm{f}\)) por la longitud de onda (\(\mathrm{λ}\)):

\[\mathrm{v=fλ}\]

También sabemos que el impulso clásico pp viene dado por p=mvp=mv que se relaciona con la fuerza a través de la segunda ley de Newton:\(\mathrm{F=\dfrac{dp}{dt}}\)

Las ondas EM con frecuencias más altas transportan más energía. Este es un resultado directo de las ecuaciones anteriores. Ya que\(\mathrm{v∝f}\) encontramos que las frecuencias más altas implican mayor velocidad. Si se incrementa la velocidad entonces tenemos mayor impulso lo que implica una mayor fuerza (se vuelve un poco complicado cuando hablamos de partículas que se acercan a la velocidad de la luz, pero esta observación se mantiene en el sentido clásico). Dado que la energía es la capacidad de un objeto para hacer trabajo, encontramos que para\(\mathrm{W=Fd}\) una mayor fuerza se correlaciona con una mayor transferencia de energía. Nuevamente, este es un fenómeno fácil de experimentar empíricamente; ¡solo párate frente a una ola más rápida y siente la diferencia!

Puntos Clave

• Una onda puede ser pensada como una perturbación u oscilación que viaja a través del espacio-tiempo, acompañada de una transferencia de energía.
• La dirección que se propaga una onda es perpendicular a la dirección en la que oscila para las ondas transversales.
• Una onda no mueve la masa en la dirección de propagación; transfiere energía.
• Las ondas transversales oscilan en el plano z-y pero viajan a lo largo del eje x.
• Una onda transversal tiene una velocidad de propagación dada por la ecuación\(\mathrm{v = fλ}\).
• La dirección de transferencia de energía es perpendicular al movimiento de la ola.
• Mientras que las ondas longitudinales oscilan en la dirección de propagación, no desplazan la masa ya que las oscilaciones son pequeñas e implican una posición de equilibrio.
• Las 'ondas' longitudinales pueden conceptualizarse como pulsos que transfieren energía a lo largo del eje de propagación.
• Las ondas longitudinales pueden conceptualizarse como ondas de presión caracterizadas por compresión y rarefacción.
• Las partículas que forman una ola de agua se mueven en caminos circulares.
• Si las olas se mueven más despacio que el viento sobre ellas, la energía se transfiere del viento a las olas.
• Las oscilaciones son mayores en la superficie de la ola y se vuelven más débiles más profundas en el fluido.
• La longitud de onda es el periodo espacial de la onda.
• La frecuencia de una onda se refiere al número de ciclos por unidad de tiempo y no debe confundirse con la frecuencia angular.
• La velocidad de fase se puede expresar como el producto de longitud de onda y frecuencia.
• Las olas que son más masivas transfieren más energía.
• Las olas con mayores velocidades transfieren más energía.
• La energía de una ola se transporta en la dirección del transporte de las olas.

Términos Clave

• medio: El material o espacio vacío por el que pasan señales, ondas o fuerzas.
• dirección de propagación: El eje a lo largo del cual se desplaza la onda.
• onda: Una perturbación en movimiento en el nivel de energía de un campo.
• longitud de onda: La longitud de un solo ciclo de una onda, medida por la distancia entre un pico o valle de una onda y el siguiente; a menudo se designa en física como λ, y corresponde a la velocidad de la onda dividida por su frecuencia.
• abrevadero: Una depresión larga y estrecha entre olas o crestas.
• velocidad de propagación: La velocidad a la que una ola se mueve a través de un medio.
• cresta: La cresta o la parte superior de una ola.
• onda transversal: Cualquier onda en la que la dirección de la perturbación sea perpendicular a la dirección de desplazamiento.
• rarefacción: una reducción en la densidad de un material, especialmente la de un fluido
• Longitudinal: Corriendo en la dirección del eje largo de un cuerpo.
• compresión: aumentar la densidad; el acto de comprimir, o el estado de ser comprimido; compactación
• velocidad de fase: La velocidad de propagación de una onda sinusoidal pura de extensión infinita y amplitud infinitesimal.
• velocidad de grupo: La velocidad de propagación de la envolvente de una onda viajera modulada, la cual se considera como la velocidad de propagación de la información o energía contenida en ella.
• onda plana: Una onda de frecuencia constante cuyos frentes de onda (superficies de fase constante) son planos paralelos infinitos de amplitud pico a pico constante normal al vector de velocidad de fase.
• velocidad de onda: El valor absoluto de la velocidad a la que viaja la fase de cualquier componente de frecuencia de la onda.
• longitud de onda: La longitud de un solo ciclo de una onda, medida por la distancia entre un pico o valle de una onda y el siguiente; a menudo se designa en física como λ, y corresponde a la velocidad de la onda dividida por su frecuencia.
• frecuencia: El cociente del número de veces n un fenómeno periódico se produce a lo largo del tiempo t en que ocurre:\(\mathrm{f = \frac{n}{t}}\).
• energía: Una cantidad que denota la capacidad de hacer trabajo y se mide en una unidad dimensionada en masa × distancia²/tiempo² (ML²/T²) o el equivalente.
• potencia: Una medida de la tasa de trabajo o transferencia de energía.
• trabajo: Una medida de la energía gastada en mover un objeto; más comúnmente, fuerza veces desplazamiento. No se realiza ningún trabajo si el objeto no se mueve.

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• Olas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Waves. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ola. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Olas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Waves. Licencia: CC BY-SA: Atribución-CompartirIgual
• dirección de propagación. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Dirección%20de%20Propagación. Licencia: CC BY-SA: Atribución-CompartirIgual
• ola. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• mediano. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/medium. Licencia: CC BY-SA: Atribución-CompartirIgual
• Animación simple de movimiento armónico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Simple_Harmonic_Motion_Animation.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• La Ecuación de Onda. Ubicado en: http://www.youtube.com/watch?v=jEEPp0mBCdg. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• cresta. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/crest. Licencia: CC BY-SA: Atribución-CompartirIgual
• Onda transversal. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Transversse_Wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Onda transversal. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Transversse_Wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Onda transversal. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Transversse_Wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicada en: www.boundless.com//physics/fsica, velocidad-de-propagacion. Licencia: CC BY-SA: Atribución-CompartirIgual
• dirección de propagación. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Dirección%20de%20Propagación. Licencia: CC BY-SA: Atribución-CompartirIgual
• longitud de onda. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/longitud de onda. Licencia: CC BY-SA: Atribución-CompartirIgual
• abrevadero. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/canal. Licencia: CC BY-SA: Atribución-CompartirIgual
• onda transversal. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/transverse_wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Animación simple de movimiento armónico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Simple_Harmonic_Motion_Animation.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• La Ecuación de Onda. Ubicado en: http://www.youtube.com/watch?v=jEEPp0mBCdg. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: Simple.wikipedia.org/wiki/Archivo:Wave.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• ComplejosInatimeAxe. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Complexsininatimeaxe.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• Onda longitudinal. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Longitudinal_Wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ondas sonoras. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Sound_Waves%23Longitudinal_and_transverse_waves. Licencia: CC BY-SA: Atribución-CompartirIgual
• Longitudinal. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/Longitudinal. Licencia: CC BY-SA: Atribución-CompartirIgual
• compresión. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/compression. Licencia: CC BY-SA: Atribución-CompartirIgual
• rarefacción. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/rarefaction. Licencia: CC BY-SA: Atribución-CompartirIgual
• Animación simple de movimiento armónico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Simple_Harmonic_Motion_Animation.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• La Ecuación de Onda. Ubicado en: http://www.youtube.com/watch?v=jEEPp0mBCdg. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: Simple.wikipedia.org/wiki/Archivo:Wave.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• ComplejosInatimeAxe. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Complexsininatimeaxe.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• funwaves - 5.nOnda longitudinal. Proporcionado por: Wikispaces. Ubicado en: http://funwaves.wikispaces.com/5.+Longitudinal+wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Poder de las olas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave_Power. Licencia: CC BY-SA: Atribución-CompartirIgual
• Poder de las olas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave_Power. Licencia: CC BY-SA: Atribución-CompartirIgual
• Poder de las olas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave_Power. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ola de viento. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wind_wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Poder de las olas. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Wave_power. Licencia: CC BY-SA: Atribución-CompartirIgual
• onda plana. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Plane%20Wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• velocidad de fase. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/phase_velocity. Licencia: CC BY-SA: Atribución-CompartirIgual
• velocidad de grupo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/group_velocity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Animación simple de movimiento armónico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Simple_Harmonic_Motion_Animation.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• La Ecuación de Onda. Ubicado en: http://www.youtube.com/watch?v=jEEPp0mBCdg. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: Simple.wikipedia.org/wiki/Archivo:Wave.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: No Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• ComplejosInatimeAxe. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Complexsininatimeaxe.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• funwaves - 5.nOnda longitudinal. Proporcionado por: Wikispaces. Ubicado en: http://funwaves.wikispaces.com/5.+Longitudinal+wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave. Licencia: CC BY: Atribución
• Vista oblicua de onda plana. Proporcionado por: Wikimedia. Ubicado en: Commons.wikimedia.org/wiki/Archivo:Plane_Wave_Oblique_View.jpg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Trayectoria elíptica sobre ondulaciones. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Trayectory_Elliptical_on_ripples.svg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Frecuencia. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Frequency. Licencia: CC BY-SA: Atribución-CompartirIgual
• Frecuencia. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Frequency. Licencia: CC BY-SA: Atribución-CompartirIgual
• Velocidad de fase. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Phase_velocity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Velocidad de grupo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Group_velocity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Frecuencia. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Frequency. Licencia: CC BY-SA: Atribución-CompartirIgual
• Frecuencia. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Frequency. Licencia: CC BY-SA: Atribución-CompartirIgual
• longitud de onda. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/longitud de onda. Licencia: CC BY-SA: Atribución-CompartirIgual
• velocidad de las olas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave%20Speed. Licencia: CC BY-SA: Atribución-CompartirIgual
• frecuencia. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/frequency. Licencia: CC BY-SA: Atribución-CompartirIgual
• Animación simple de movimiento armónico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Simple_Harmonic_Motion_Animation.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• La Ecuación de Onda. Ubicado en: http://www.youtube.com/watch?v=jEEPp0mBCdg. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: Simple.wikipedia.org/wiki/Archivo:Wave.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• ComplejosInatimeAxe. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Complexsininatimeaxe.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• funwaves - 5.nOnda longitudinal. Proporcionado por: Wikispaces. Ubicado en: http://funwaves.wikispaces.com/5.+Longitudinal+wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave. Licencia: CC BY: Atribución
• Vista oblicua de onda plana. Proporcionado por: Wikimedia. Ubicado en: Commons.wikimedia.org/wiki/Archivo:Plane_Wave_Oblique_View.jpg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Trayectoria elíptica sobre ondulaciones. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Trayectory_Elliptical_on_ripples.svg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Velocidad de grupo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Group_velocity. Licencia: CC BY: Atribución
• Ondas sinusoidales diferentes frecuencias. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Sine_Waves_diferent_frecuencias.svg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Radiación electromagnética. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Radiación_Electromagnética. Licencia: CC BY-SA: Atribución-CompartirIgual
• Radiación electromagnética. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Electromagnetic_radiation. Licencia: CC BY-SA: Atribución-CompartirIgual
• energía. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/energy. Licencia: CC BY-SA: Atribución-CompartirIgual
• trabajo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/work. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicada en: www.boundless.com//sociología/· power. Licencia: CC BY-SA: Atribución-CompartirIgual
• Animación simple de movimiento armónico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Simple_Harmonic_Motion_Animation.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• La Ecuación de Onda. Ubicado en: http://www.youtube.com/watch?v=jEEPp0mBCdg. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: http://simple.Wikipedia.org/wiki/File:Wave.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• ComplejosInatimeAxe. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/File:ComplexSinInATimeAxe.gif. Licencia: Dominio Público: No Conocido Derechos de Autor
• funwaves - 5.nOnda longitudinal. Proporcionado por: Wikispaces. Ubicado en: http://funwaves.wikispaces.com/5.+Longitudinal+wave. Licencia: CC BY-SA: Atribución-CompartirIgual
• Dos Tipos de Ondas: Longitudinal vs Transversal. Ubicado en: http://www.youtube.com/watch?v=PxB8-BVO82g. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ola. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Wave. Licencia: CC BY: Atribución
• Vista oblicua de onda plana. Proporcionado por: Wikimedia. Ubicado en: Commons.wikimedia.org/wiki/Archivo:Plane_Wave_Oblique_View.jpg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Trayectoria elíptica sobre ondulaciones. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/File:Elliptical_trajectory_on_ripples.svg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Velocidad de grupo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Group_velocity. Licencia: CC BY: Atribución
• Ondas sinusoidales diferentes frecuencias. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Sine_Waves_diferent_frecuencias.svg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Olas en pacifica 1. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Waves_en_Pacifica_1.jpg. Licencia: Dominio Público: No Conocido Derechos de Autor
• Onda electromagnética3DdesdeLado. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:OndaElectromagnética3Dfromside.gif. Licencia: CC BY: Atribución