Saltar al contenido principal
LibreTexts Español

15.7: Ondas en cuerdas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128148

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Calcular la velocidad de una ola en una cuerda

    Al estudiar las olas, es útil usar una cuerda para observar visualmente las propiedades físicas de las olas. Imagina que estás sosteniendo un extremo de una cuerda, y el otro extremo está asegurado y la cuerda está apretada. Ahora bien, si tuvieras que mover la cuerda ya sea hacia arriba y hacia abajo. La onda que se produce debido a este movimiento se llama onda transversal. Una onda transversal se define como una onda donde el movimiento de las partículas del medio es perpendicular a la dirección de propagación de la onda. En la Figura 1 se muestra esto en un diagrama. En este caso, el medio a través del cual se propagan las olas es la cuerda. La ola viajaba de un extremo a otro, mientras que la cuerda se movía hacia arriba y hacia abajo.

    imagen

    Figura 1: En ondas transversales, el medio en el que viaja la onda se mueve perpendicular a la dirección de la onda.

    Propiedades de la onda

    Las ondas transversales tienen lo que se llaman picos y valles. El pico es la cresta, o punto superior de la ola y el valle es el valle o punto inferior de la ola. Refiérase a la Figura 2 para una representación visual de estos términos.La amplitud es el desplazamiento máximo de una partícula desde su posición de equilibrio.La longitud de onda, generalmente denotada con una lambda (λ) y medida en metros, es la distancia de un pico al siguiente pico, o de un valle al siguiente canal. Periodo, generalmente denotado como T y medido en segundos, es el tiempo que tarda dos picos sucesivos, o una longitud de onda, en pasar por un punto fijo.La frecuencia, f, es el número de longitudes de onda que pasan por un punto dado en 1 segundo. La frecuencia se mide tomando el recíproco de un período:\(\mathrm{f=\frac{1}{T}}\)

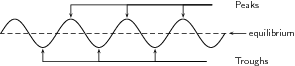
    imagen

    Figura 2: Los picos son los puntos más altos de las olas y los valles son el fondo, o valles de las olas.

    Velocidad de una ola en una cuerda

    La velocidad se encuentra dividiendo la distancia recorrida por el tiempo que tardó en recorrer esa distancia. En ondas, esto se encuentra dividiendo la longitud de onda por el periodo: v=λTV=λtPodemos tomar la proporcionalidad inversa a periodo y frecuencia y aplicarla a esta situación:

    \[\begin{align} & \mathrm{v=\dfrac{λ}{T}} \\ & \mathrm{ v=λ\dfrac{1}{T}} \\ & \mathrm{ v=λf} \end{align}\]

    Velocidad de una ola en una cuerda vibratoria

    Otro ejemplo de ondas en cuerdas son las de las ondas en cuerdas vibrantes, como en instrumentos musicales. Tanto los pianos como las guitarras utilizan cuerdas vibratorias para producir música. En estos casos, la frecuencia es lo que caracteriza al tono y por lo tanto a la nota. La velocidad de una onda en este tipo de cuerda es proporcional a la raíz cuadrada de la tensión en la cuerda e inversamente proporcional a la raíz cuadrada de la densidad lineal de la cuerda:\(\mathrm{v=\sqrt{\frac{T}{μ}}}\)

    Reflexiones

    Cuando las ondas transversales en cuerdas se encuentran con un extremo, se reflejan, y cuando la onda incidente se encuentra con la onda reflejada, se produce interferencia.

    objetivos de aprendizaje

    • Explicar cuándo ocurre una onda estacionaria

    Visión general

    Imagina que estás sosteniendo un extremo de una cuerda, y el otro extremo está asegurado y la cuerda está apretada. Ahora bien, si tuvieras que mover la cuerda ya sea hacia arriba y hacia abajo. La onda que se produce debido a este movimiento se llama onda transversal. Una onda transversal se define como una onda donde el movimiento de las partículas del medio es perpendicular a la dirección de la propagación de la onda. lo muestra en un diagrama. En este caso, el medio a través del cual se propagan las olas es la cuerda. La ola viajaba de un extremo a otro, mientras que la cuerda se movía hacia arriba y hacia abajo.

    imagen

    Onda Transversal: Diagrama de una onda transversal. El movimiento de la ola se mueve perpendicular al medio en el que viaja.

    Propiedades de Waves

    • Las ondas transversales tienen lo que se llaman picos y valles. El pico es la cresta, o punto superior de la ola y el valle es el valle o punto inferior de la ola.
    • La amplitud es el desplazamiento máximo de una partícula desde su posición de equilibrio.
    • La longitud de onda, generalmente denotada con lambda (λ) y medida en metros, es la distancia de un pico al siguiente pico, o de un valle al siguiente valle.
    • Período, generalmente denotado como T y medido en segundos, es el tiempo que tarda dos picos sucesivos, o una longitud de onda, en pasar por un punto fijo.
    • Frecuencia, f, es el número de longitudes de onda que pasan por un punto dado en 1 segundo. La frecuencia se mide tomando el recíproco de un período:\(\mathrm{f=\frac{1}{T}}\)
    • Las ondas transversales pueden ocurrir mientras se fijan en el punto final o mientras están libres en el punto final.

    Reflexiones de ondas transversales

    La forma en que se refleja una onda transversal depende de si se fija o no en ambos extremos. Primero veremos las olas que se fijan en ambos extremos:

    muestra una imagen de una onda transversal que se refleja desde un extremo fijo. Cuando una onda transversal se encuentra con un extremo fijo, la onda se refleja, pero se invierte. Esto intercambia los picos con los valles y los valles con los picos.

    imagen

    Onda Transversal Con Punto Final Fijo: Onda transversal que se fija en el punto final. La onda reflejada se invierte.

    es una imagen de una onda transversal en una cuerda que se encuentra con un extremo libre. La onda se refleja, pero a diferencia de una onda transversal con un extremo fijo, no se invierte.

    imagen

    Onda Transversal Con Extremo Libre: Cuando una onda transversal se encuentra con un extremo libre, se refleja.

    Ondas Standing

    Cuando se produce cualquiera de los dos escenarios de reflexión de onda, la onda incidente se encuentra con la onda reflejada. Estas ondas se mueven una junto a la otra en direcciones opuestas, provocando interferencias. Cuando estas dos ondas tienen la misma frecuencia, el producto de esto se llama las ondas estacionarias. Las olas estacionarias parecen estar quietas, de ahí el nombre. Para entender cómo ocurren las ondas estacionarias, podemos analizarlas más a fondo: Cuando la onda incidente y la onda reflejada se encuentran por primera vez, ambas ondas tienen una amplitud es cero. A medida que las olas continúan moviéndose entre sí, continúan interfiriendo entre sí ya sea constructivamente o destructivamente.

    Como recordarás de átomos anteriores, cuando las ondas están completamente en fase e interfieren entre sí de manera constructiva, se amplifican, y cuando están completamente desfasadas e interfieren destructivamente cancelan. A medida que las olas continúan moviéndose entre sí, y se reflejan desde el extremo opuesto, continúan interfiriendo en ambos sentidos, y se produce una onda estacionaria.

    Cada punto en el medio que contiene una onda estacionaria oscila hacia arriba y hacia abajo y la amplitud de las oscilaciones depende de la ubicación del punto. Cuando observamos ondas estacionarias sobre cuerdas, parece que la ola no se mueve y se queda quieta. El principio de las ondas estacionarias es la base de la resonancia y cuántos instrumentos musicales obtienen su sonido. Los puntos en una onda estacionaria que parecen permanecer planos y no se mueven se denominan nodos. Los puntos que alcanzan la altura máxima de oscilación se denominan antinodos.

    Puntos Clave

    • El tipo de onda que ocurre en una cuerda se llama onda transversal. En una onda transversal, la dirección de la onda es perpendicular a la dirección en la que oscila la cuerda.
    • El periodo de una onda es indirectamente proporcional a la frecuencia de la onda:\(\mathrm{T=\frac{1}{f}}\).
    • La velocidad de una onda es proporcional a la longitud de onda e indirectamente proporcional al periodo de la onda:\(\mathrm{v=\frac{λ}{T}}\).
    • Esta ecuación se puede simplificar utilizando la relación entre frecuencia y período:\(\mathrm{v=λf}\).
    • Cuando una onda transversal en una cuerda se fija en el punto final, la onda reflejada se invierte de la onda incidente. Cuando una onda transversal en una cuerda está libre en el punto final, la onda reflejada no se invierte de la onda incidente.
    • Una onda estacionaria ocurre cuando una onda incidente se encuentra con una onda reflejada en una cuerda.
    • Los puntos en una onda estacionaria que parecen permanecer planos y no se mueven se denominan nodos. Los puntos que alcanzan la altura máxima de oscilación se denominan antinodos.
    • Cada punto en el medio que contiene una onda estacionaria oscila hacia arriba y hacia abajo y la amplitud de las oscilaciones depende de la ubicación del punto.
    • Una onda estacionaria tiene algunos puntos que permanecen planos debido a la interferencia destructiva. Estos se llaman antinodos.
    • Los puntos en una onda estacionaria que han alcanzado la máxima oscilación lo hacen a partir de interferencias constructivas, y se denominan nodos.

    Términos Clave

    • onda transversal: Cualquier onda en la que la dirección de la perturbación sea perpendicular a la dirección de desplazamiento.
    • oscilar: Para balancearse hacia adelante y hacia atrás, especialmente si con un ritmo regular.
    • amplitud: El valor absoluto máximo de alguna cantidad que varía.
    • onda estacionaria: Forma de onda que se produce en un medio limitado y fijo de tal manera que la onda reflejada coincide con la onda producida. Un ejemplo común es la vibración de las cuerdas en un instrumento musical de cuerda.
    • onda transversal: Cualquier onda en la que la dirección de la perturbación sea perpendicular a la dirección de desplazamiento.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    15.7: Ondas en cuerdas is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.