Saltar al contenido principal
LibreTexts Español

16.5: Otros temas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128377
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Identificar fuentes de patrones de ondas esféricas y planas

    Ondas Esféricas

    Christiaan Huygens fue un científico holandés que desarrolló una técnica útil para determinar cómo y dónde se propagan las olas. En 1678, propuso que cada punto que toca una perturbación luminosa se convierte en fuente de una onda esférica; la suma de estas ondas secundarias determina la forma de la onda en cualquier momento posterior. El Principio Huygen-Fresnel muestra que a medida que las olas interactúan entre sí, interfieren ya sea constructiva o destructivamente. La interferencia constructiva ocurre cuando las ondas están completamente en fase entre sí y amplifican las ondas. La interferencia destructiva ocurre cuando las ondas están exactamente desfasadas con cualquiera de las otras, y si las ondas están perfectamente desfasadas entre sí, la onda se cancelará por completo. Como todas las ondas provienen de una fuente puntual, las ondas ocurren en un patrón esférico. Todas las ondas provienen de una sola fuente puntual y son esféricas.

    imagen

    Onda esférica: Cuando las ondas se producen a partir de una fuente puntual, son ondas esféricas.

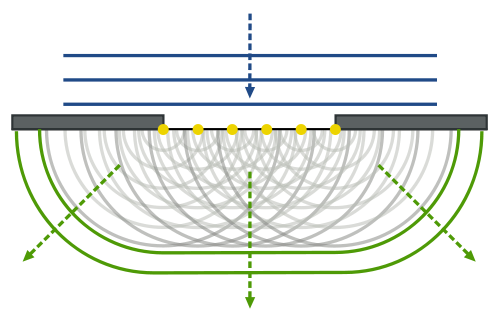
    imagen

    Principio Huygen-Fresnel: El Principio Huygen-Fresnel utiliza la ley de la refracción. Cada punto de la onda produce ondas que interfieren entre sí de manera constructiva o destructiva.

    Ondas Planas

    Una onda plana es una onda de frecuencia constante cuyos frentes de onda (superficies de fase constante) son planos paralelos infinitos de amplitud pico a pico constante normal al vector de velocidad de fase. No es posible en la práctica tener una onda plana verdadera; sólo una onda plana de extensión infinita se propagará como onda plana. Sin embargo, muchas olas son aproximadamente ondas planas en una región localizada del espacio. Por ejemplo, una fuente localizada como una antena produce un campo que es aproximadamente una onda plana lejos de la antena en su región de campo lejano. Del mismo modo, si las escalas de longitud son mucho más largas que la longitud de onda de la onda, como suele ser el caso de la luz en el campo de la óptica, se pueden tratar las ondas como rayos de luz que corresponden localmente a ondas planas.

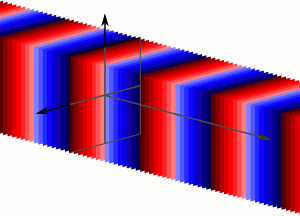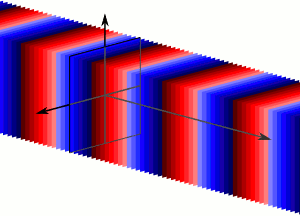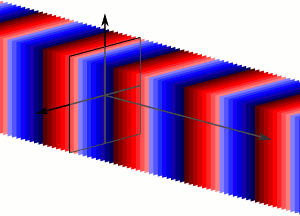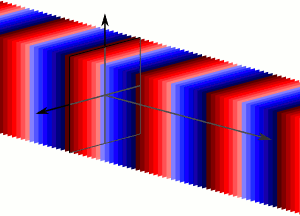
    imagen

    Onda plana: Las ondas planas son un número infinito de frentes de onda normales a la dirección de la proposición.

    Ondas estacionadas en una cuerda

    La onda estacionaria se produce debido a la interferencia cuando las ondas transversales en las cuerdas se reflejan y las ondas incidentes y reflejadas se encuentran.

    objetivos de aprendizaje

    • Identificar cuándo ocurre una onda estacionaria

    Una onda estacionaria es una onda que aparece estacionaria, lo que significa que permanece en una posición constante. En una cuerda, una onda estacionaria es un tipo de onda transversal, donde el movimiento de las partículas del medio es perpendicular a la dirección de propagación de la onda. Una onda estacionaria puede ocurrir cuando dos ondas idénticas que se mueven en diferentes direcciones a lo largo de la cuerda interfieren.

    Hay dos escenarios de ondas en las cuerdas: la cuerda se fija en ambos extremos, o la cuerda se fija en un extremo y libre en el otro. Una onda transversal se moverá a lo largo de la cuerda hasta que llegue al otro extremo. Luego se refleja desde ese extremo y comienza a retroceder hacia la dirección original; en este punto se produce interferencia. muestra una onda transversal que se refleja desde un extremo fijo. Cuando una onda transversal se encuentra con un extremo fijo, la onda se refleja, pero se invierte. Esto intercambia los picos con los valles y los valles con los picos. Diagrama una onda transversal en una cuerda que se encuentra con un extremo libre. La onda se refleja, pero a diferencia de una onda transversal con un extremo fijo, no se invierte.

    imagen

    Reflejo Final Libre: La onda se refleja, pero a diferencia de una onda transversal con un extremo fijo, no se invierte.

    imagen

    Reflexión de extremo fijo: Cuando una onda transversal se encuentra con un extremo fijo, la onda se refleja, pero se invierte.

    Ondas Estacionales

    Cuando se produce cualquiera de los dos escenarios de reflexión de onda, la onda incidente se encuentra con la onda reflejada. Estas ondas se mueven una junto a la otra en direcciones opuestas, provocando interferencias. Cuando estas dos ondas tienen la misma frecuencia, el producto de esto se llama las ondas estacionarias. Las ondas estacionarias parecen estar quietas, de ahí el nombre. ilustra una onda estacionaria de movimiento muy lento. (Una aplicación del principio de ondas estacionarias está en la música con el concepto de resonancia y cuántos instrumentos musicales, como guitarras y pianos, obtienen su sonido). Examinemos ahora cómo ocurren las ondas estacionarias.

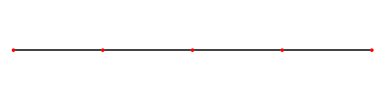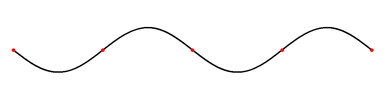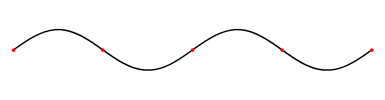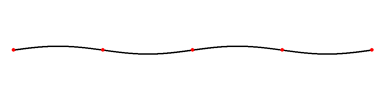
    imagen

    Onda estacionaria sobre una cuerda: así es como se vería una onda estacionaria si la redujeras la velocidad. La ola es causada por una onda incidente en una cuerda que se refleja y luego viaja de regreso en la dirección de la que vino. Entonces las dos olas se encuentran e interfieren entre sí provocando este fenómeno.

    Interferencia constructiva vs. destructiva

    Cuando la onda incidente y la onda reflejada se encuentran por primera vez, ambas ondas tienen una amplitud es cero. A medida que las olas continúan moviéndose entre sí, continúan interfiriendo entre sí, ya sea constructivamente o destructivamente. Como se discutió en átomos anteriores, cuando las ondas están completamente en fase e interfieren entre sí constructivamente se amplifican, y cuando están completamente desfasadas e interfieren destructivamente se cancelan. A medida que las olas continúan moviéndose entre sí, y se reflejan desde el extremo opuesto, continúan interfiriendo en ambos sentidos; se produce una onda estacionaria. Cada punto en el medio que contiene una onda estacionaria oscila hacia arriba y hacia abajo, y la amplitud de las oscilaciones depende de la ubicación del punto. Cuando observamos una onda estacionaria sobre cuerdas, parece que la ola no se mueve sino que se queda quieta. En resumen:

    • Los puntos que alcanzan la altura máxima de oscilación se denominan antinodos, y son el resultado de una interferencia constructiva completa.
    • Los puntos en una onda estacionaria que parecen permanecer planos y no se mueven se denominan nodos. Estos se deben a la completa interferencia destructiva.

    Ondas estacionarias en columnas de aire

    Ondas estacionarias en columnas de aire es el fenómeno físico que da a los instrumentos de viento su resonancia y, por tanto, sonido.

    objetivos de aprendizaje

    • Identificar el tipo de onda estacionaria en una columna de aire

    Ondas Estacionales

    Una onda estacionaria es una onda que parece estar estacionaria, lo que significa que permanece en una posición constante. En una columna de aire, una onda estacionaria puede formarse como una onda longitudinal o transversal. Una onda transversal, tal vez recuerdes, es una onda donde el movimiento de las partículas del medio es perpendicular a la dirección de propagación de la onda. Una onda longitudinal, por otro lado, es paralela a la dirección de propagación. Una onda estacionaria puede ocurrir cuando dos ondas idénticas que se mueven en diferentes direcciones interfieren.

    Columnas de aire

    Cuando se forma una onda estacionaria en un tubo, la onda estacionaria tiene un desplazamiento máximo de aire en el extremo abierto llamado antinodo. Aquí, el movimiento no está restringido. En el extremo cerrado, no hay desplazamiento; esto se llama nodo, y el aire se detiene. La distancia desde un nodo hasta el antinodo es 1/4 de una longitud de onda, y es igual a la longitud del tubo.

    muestra que esta resonancia puede ser producida por una vibración introducida en o cerca del extremo cerrado del tubo también. Esto se considera una vibración natural de la columna de aire independientemente de cómo se induzca. Dado que los desplazamientos máximos de aire son posibles en el extremo abierto y ninguno en el extremo cerrado, existen otras longitudes de onda más cortas que pueden resonar en el tubo. Por ejemplo, una onda estacionaria puede tener tres cuartos de su longitud de onda en el tubo, o L= (3/4) λ. Esto se puede renderizar de la siguiente manera:

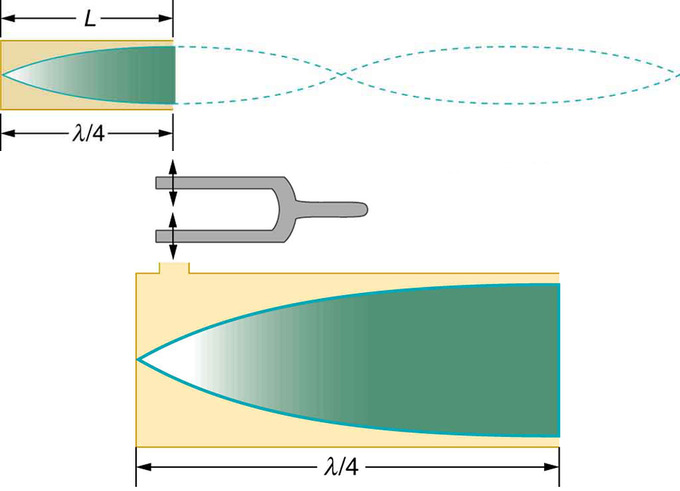
    imagen

    Onda Permanente en Columna de Aire: La misma onda estacionaria se crea en el tubo por una vibración introducida cerca de su extremo cerrado.

    \[\lambda ^ { \prime } = \dfrac { 4 \mathrm { L } } { 3 }\]

    Continuando con este proceso revela toda una serie de sonidos de menor longitud de onda y frecuencia más alta que resuenan en el tubo. Utilizamos términos específicos para las resonancias en cualquier sistema. La frecuencia resonante más baja se llama fundamental, mientras que todas las frecuencias resonantes más altas se llaman armónicos. Todas las frecuencias resonantes son múltiplos integrales de lo fundamental, y se denominan colectivamente armónicos. El fundamental es el primer armónico, el primer armónico es el segundo armónico, y así sucesivamente. muestra cómo lo fundamental y los tres primeros armónicos (los primeros cuatro armónicos) en un tubo cerrado en un extremo.

    imagen

    Los primeros cuatro armónicos: El fundamental y los tres armónicos más bajos para un tubo cerrado en un extremo. Todos tienen desplazamientos máximos de aire en el extremo abierto y ninguno en el extremo cerrado.

    Ahora busquemos un patrón en las frecuencias resonantes para un tubo simple que esté cerrado en un extremo. El fundamental tiene =4L, y la frecuencia está relacionada con la longitud de onda y la velocidad del sonido según lo dado por lo siguiente:

    \[\mathbf { v } _ { \mathrm { w } } = \mathrm { f } \lambda\]

    Resolver para f en esta ecuación da una forma más útil:

    \[\mathrm { f } = \dfrac { \mathrm { v } _ { \mathrm { w } } } { \lambda } = \dfrac { \mathbf { v } _ { \mathrm { w } } } { 4 \mathrm { L } }\]

    Aquí, f es la frecuencia, v w es la velocidad del sonido en el aire, λ es la longitud de onda y L es la longitud de la columna de aire. El primer sobretono tiene = 4L/3. De esto, podemos deducir lo siguiente:

    \[\mathrm { f } ^ {\prime } = 3 \dfrac { v _ { \mathrm { w } } } { 4 \mathrm { L } } = 3 \mathrm { f }\]

    Debido a que f′ = 3f, llamamos al primer armónico el tercer armónico. Continuando con este proceso, vemos un patrón que puede generalizarse en una sola expresión. Las frecuencias resonantes de un tubo cerrado en un extremo son:

    \[\mathrm { f } _ { \mathrm { n } } = \mathrm { n } \dfrac { \mathrm { vw } } { 4 \mathrm { L } } , \mathrm { n } = 1,3,5\]

    Aquí, f1 es lo fundamental, f3 es el primer armónico, y así sucesivamente. Es interesante que las frecuencias resonantes dependan de la velocidad del sonido y, por ende, de la temperatura. Esta dependencia plantea un problema notable para los órganos en antiguas catedrales sin calefacción, y también es la razón por la que los músicos suelen llevar sus instrumentos de viento a temperatura ambiente antes de tocarlos.

    Ejemplo\(\PageIndex{1}\):

    El fundamental y armónicos pueden estar presentes simultáneamente en una variedad de combinaciones. Por ejemplo, la C media en una trompeta tiene un sonido distintivamente diferente del C medio en un clarinete, siendo ambos instrumentos versiones modificadas de un tubo cerrado en un extremo. La frecuencia fundamental es la misma (y suele ser la más intensa), pero los armónicos y su mezcla de intensidades son diferentes y están sujetos a sombreado por parte del músico. Esta mezcla es lo que le da a diversos instrumentos musicales (y voces humanas) sus características distintivas, ya sea que tengan columnas de aire, cuerdas, cajas de sondeo o parche de batería. De hecho, gran parte de nuestro discurso está determinado por dar forma a la cavidad que forman la garganta y la boca y posicionar la lengua para ajustar lo fundamental y la combinación de armónicos. Se pueden hacer cavidades resonantes simples para resonar con el sonido de las vocales, por ejemplo.

    Vibraciones forzadas y resonancia

    El fenómeno de conducir un sistema con una frecuencia igual a su frecuencia natural se llama resonancia.

    objetivos de aprendizaje

    • Explicar la relación entre la curva de resonancia y la amortiguación

    Vibración forzada y resonancia

    Mucha gente ha jugado con juguetes que involucran un objeto sostenido por una banda elástica: algo así como la pelota de pádel suspendida de un dedo adentro. Digamos que una persona conduce la pelota de pádel moviendo su dedo hacia arriba y hacia abajo con cierta frecuencia. En este ejemplo, él o ella está provocando una oscilación forzada (o vibración). Al principio el dedo se mantiene firme, y la pelota rebota arriba y abajo con una pequeña cantidad de amortiguación. Si el dedo se mueve hacia arriba y hacia abajo lentamente, la pelota seguirá sin rebotar mucho por sí sola.

    imagen

    Bolas de paleta y frecuencias: La pelota de pádel en su banda de goma se mueve en respuesta al dedo que la sostiene. Si el dedo se mueve con la frecuencia natural f0 de la pelota en la banda elástica, entonces se logra una resonancia, y la amplitud de las oscilaciones de la pelota aumenta dramáticamente. A frecuencias de conducción más altas y más bajas, la energía se transfiere a la bola de manera menos eficiente y responde con oscilaciones de menor amplitud.

    A medida que aumenta la frecuencia a la que se mueve el dedo hacia arriba y hacia abajo, la pelota responderá oscilando con amplitud creciente. Después de conducir la pelota a su frecuencia natural, las oscilaciones de la pelota aumentan en amplitud con cada oscilación mientras sea conducida. El fenómeno de conducir un sistema con una frecuencia igual a su frecuencia natural se llama resonancia. A medida que la frecuencia de conducción se vuelve progresivamente más alta que la frecuencia resonante o natural, la amplitud de las oscilaciones se vuelve más pequeña hasta que las oscilaciones casi desaparecen y el dedo simplemente se mueve hacia arriba y hacia abajo con poco efecto sobre la pelota.

    Efectos de la Amortiguación

    En la vida real, la mayoría de los osciladores tienen amortiguación presente en el sistema. Es interesante que las anchuras de las curvas de resonancia mostradas en dependen de la amortiguación: cuanto menor sea la amortiguación, más estrecha será la resonancia. Para que un oscilador accionado resuene a una frecuencia muy específica, es necesario que haya la menor amortiguación posible, como es el caso de las cuerdas de piano y muchos otros instrumentos musicales. Por el contrario, para oscilaciones de pequeña amplitud, como en el sistema de suspensión de un automóvil, es necesario que haya una amortiguación pesada. La amortiguación pesada reduce la amplitud, pero la compensación es que el sistema responde a más frecuencias.

    imagen

    Amortiguación: La amplitud de un oscilador armónico es función de la frecuencia de la fuerza motriz. Las curvas representan el mismo oscilador con la misma frecuencia natural pero con diferentes cantidades de amortiguación. La resonancia ocurre cuando la frecuencia de conducción es igual a la frecuencia natural, y la mayor respuesta es para la menor cantidad de amortiguación. La respuesta más estrecha es también para la menor cantidad de amortiguación.

    Ejemplo\(\PageIndex{2}\):

    Estas características de los osciladores armónicos impulsados se aplican a una gran variedad de sistemas. Al sintonizar una radio, por ejemplo, las personas están ajustando la frecuencia resonante del circuito de radio para que solo oscile a la frecuencia de transmisión (o conducción) de la estación deseada. Cuanto más selectiva sea la radio en la discriminación entre estaciones, menor será su amortiguación. Un niño en un columpio es conducido por un padre a la frecuencia natural del swing para lograr la máxima amplitud. En todos estos casos, la eficiencia de la transferencia de energía de la fuerza impulsora al oscilador es mejor en resonancia. En caminos de grava que están corrugados, si la gente viaja a la velocidad 'equivocada', los baches son muy notorios. A otras velocidades, es difícil sentir los baches en absoluto. muestra una fotografía de un famoso ejemplo (el Puente Tacoma Narrows) de los efectos destructivos de una oscilación armónica impulsada. Desafortunadamente, los fuertes vientos pasaron a conducir el puente a su frecuencia natural, lo que llevó al colapso.

    imagen

    Colapso del puente Tacoma Narrows: En 1940, el puente Tacoma Narrows en el estado de Washington se derrumbó. Los fuertes vientos cruzados condujeron al puente a oscilaciones a su frecuencia resonante. La amortiguación disminuyó cuando los cables de soporte se soltaron y comenzaron a deslizarse sobre las torres, permitiendo amplitudes cada vez mayores hasta que la estructura falló. (crédito: PRI Studio 360, vía Flickr)

    Puntos Clave

    • Las ondas interfieren entre sí de manera constructiva o destructiva, lo que amplificará o minimizará la onda, respectivamente.
    • Las ondas esféricas se emiten desde una única fuente puntual en forma esférica.
    • Una onda plana es una onda de frecuencia constante cuyos frentes de onda (superficies de fase constante) son planos paralelos infinitos de amplitud pico a pico constante normal al vector de velocidad de fase.
    • Aunque en la práctica no es posible tener una onda plana verdadera, muchas ondas se aproximan al comportamiento de las ondas planas.
    • La onda reflejada se invierte de la onda incidente cuando una onda transversal en una cuerda se fija en el punto final. La onda reflejada no se invierte de la onda incidente cuando una onda transversal en una cuerda está libre en el punto final.
    • Una onda estacionaria ocurre cuando una onda incidente se encuentra con una onda reflejada en una cuerda.
    • Una onda estacionaria contiene nodos (puntos que permanecen planos debido a la interferencia destructiva) y antinodos (puntos con oscilación máxima debido a la interferencia constructiva).
    • Cada punto de la cuerda oscila hacia arriba y hacia abajo y la amplitud de las oscilaciones depende de la ubicación del punto.
    • Una onda estacionaria tiene algunos puntos que permanecen planos debido a la interferencia destructiva. Estos se llaman antinodos.
    • Los puntos en una onda estacionaria que han alcanzado la máxima oscilación lo hacen a partir de interferencias constructivas, y se denominan nodos.
    • Una onda estacionaria en una columna de aire es una onda transversal.
    • Un nodo ocurre en el extremo cerrado de un tubo de aire donde no hay desplazamiento de onda.
    • Un antinodo ocurre en el extremo abierto del tubo de aire donde se produce el desplazamiento máximo.
    • Las frecuencias resonantes de un tubo cerrado en un extremo son las siguientes:\(\mathrm { f } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { vw } } { 4 \mathrm { L } }\), n=1,3,5.
    • Cualquier oscilador tiene una frecuencia natural. Impulsadas a la frecuencia natural, las oscilaciones aumentan en amplitud con cada oscilación.
    • Los anchos de las curvas de resonancia dependen de la amortiguación: menos amortiguación corresponde a una resonancia más estrecha. Con menos amortiguación, el pico de resonancia se vuelve más pronunciado.
    • La relación entre resonancia y amortiguación se aplica a una gran variedad de sistemas. La amortiguación a menudo se reduce o mejora para inducir la respuesta deseada de un oscilador.

    Términos Clave

    • frente de onda: Una superficie imaginaria que pasa por puntos de un medio que oscila en fase.
    • interferencia destructiva: Ocurre cuando las olas interfieren entre sí de cresta a valle (pico a valle) y están exactamente desfasadas entre sí.
    • interferencia constructiva: Ocurre cuando las olas interfieren entre sí cresta a cresta y las olas están exactamente en fase entre sí.
    • onda transversal: Cualquier onda en la que la dirección de la perturbación sea perpendicular a la dirección de desplazamiento.
    • frecuencia natural: La frecuencia a la que un sistema vibra por sí solo. Para un resorte (constante de resorte k) con un objeto de masa m unido, la frecuencia natural se da como\(\mathrm { f } _ { \mathrm { n } } = \frac { 1 } { 2 \pi } \sqrt { \frac { \mathrm { k } } { \mathrm { m } } }\).
    • amortiguación: La reducción en la magnitud de las oscilaciones por la disipación de energía

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 16.5: Otros temas is shared under a not declared license and was authored, remixed, and/or curated by Boundless.