Saltar al contenido principal
LibreTexts Español

17.3: Ley de Coulomb

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128094
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Aplicar el principio de superposición para determinar la respuesta neta causada por dos o más estímulos

    El principio de superposición (también conocido como propiedad de superposición) establece que: para todos los sistemas lineales, la respuesta neta en un lugar y tiempo dados causada por dos o más estímulos es la suma de las respuestas que habrían sido causadas por cada estímulo individualmente. Para la ley de Coulomb, los estímulos son fuerzas. Por lo tanto, el principio sugiere que la fuerza total es una suma vectorial de fuerzas individuales.

    Fuerza de Coulombo

    La forma escalar de la Ley de Coulomb relaciona la magnitud y el signo de la fuerza electrostática F, actuando simultáneamente sobre dos cargas puntuales q 1 y q 2:

    \[| \mathrm { F } | = \dfrac { 1 } { 4 \pi a r \epsilon _ { 0 } } \dfrac { \left| q _ { 1 } q _ { 2 } \right| } { \mathrm { r } ^ { 2 } }\]

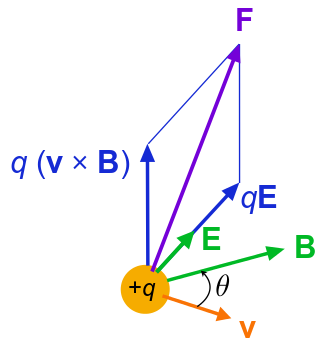
    imagen

    Fuerza de Lorentz sobre una Partícula Móvil: Lorentz fuerza f sobre una partícula cargada (de carga q) en movimiento (velocidad instantánea v). El campo E y el campo B varían en espacio y tiempo.

    donde r es la distancia de separación y ε 0 es permitividad eléctrica. Si el producto q 1 q 2 es positivo, la fuerza entre ellos es repulsiva; si q 1 q 2 es negativa, la fuerza entre ellos es atractiva. El principio de superposición lineal permite que la extensión de la ley de Coulomb incluya cualquier número de cargas puntuales, con el fin de derivar la fuerza sobre cualquier carga puntual mediante una adición vectorial de estas fuerzas individuales que actúan solas sobre esa carga puntual. El vector de fuerza resultante pasa a ser paralelo al vector de campo eléctrico en ese punto, con ese punto de carga eliminada.

    Para calcular la fuerza sobre una pequeña carga de prueba q en la posición rr, debido a un sistema de N cargas discretas:

    \[\mathrm{F(r)=\dfrac{q}{4πarϵ_0} }\sum _ { i = 1 } ^ { N } q _ { i } \frac { \mathrm { r } - \mathrm { r } _ { \mathrm { i } } } { \left| \mathrm { r } - \mathrm { r } _ { \mathrm { i } } \right| ^ { 3 } } = \frac { q } { r 4 \pi a r \epsilon _ { 0 } }\sum _ { \mathrm { i } = 1 } ^ { \mathrm { N } } \mathrm { q } _ { \mathrm { i } } \dfrac { \hat { \mathrm { R } _ { i } } } { \left| \mathrm { R } _ { \mathrm { i } } \right| ^ { 2 } }\]

    donde q i y ri son el vector de magnitud y posición de la i-ésima carga, respectivamente, y\(\hat { \mathrm { R } _ { \mathrm { i } } }\) es un vector unitario en la dirección de\(\mathrm { R } _ { \mathrm { i } } = \mathrm { r } - \mathrm { r } _ { \mathrm { i } }\) (un vector que apunta desde las cargas q i a q.)

    Por supuesto, nuestra discusión sobre la superposición de fuerzas se aplica a cualquier tipo (o combinación) de fuerzas. Por ejemplo, cuando una carga se mueve en presencia de un campo magnético así como de un campo eléctrico, la carga sentirá tanto fuerzas electrostáticas como magnéticas. La fuerza total, afectando el movimiento de la carga, será la suma vectorial de las dos fuerzas. (En este ejemplo particular de la carga móvil, la fuerza debida a la presencia de campo electromagnético se denomina colectivamente fuerza de Lorentz (ver).

    Distribución esférica de la carga

    La distribución de carga alrededor de una molécula es de naturaleza esférica y crea una especie de “nube” electrostática alrededor de la molécula.

    objetivos de aprendizaje

    • Describir la forma de una fuerza de Coulomb a partir de una distribución esférica de carga

    A través del trabajo de científicos a finales del siglo XVIII, las principales características de la fuerza electrostática —la existencia de dos tipos de carga, la observación de que cargas similares se repelen, a diferencia de las cargas atraen, y la disminución de la fuerza con la distancia— fueron finalmente refinadas y expresadas como una fórmula matemática. La fórmula matemática para la fuerza electrostática se llama ley de Coulomb según el físico francés Charles Coulomb (1736—1806), quien realizó experimentos y propuso primero una fórmula para calcularla.

    imagen

    Distribución de carga en una molécula de agua: Representación esquemática de la nube externa de electrones de una molécula de agua neutra. Los electrones pasan más tiempo cerca del oxígeno que los hidrógenos, dando una separación permanente de carga como se muestra. El agua es así una molécula polar. Se ve afectado más fácilmente por las fuerzas electrostáticas que las moléculas con distribuciones de carga uniformes.

    Los experimentos modernos han verificado la ley de Coulomb con gran precisión. Por ejemplo, se ha demostrado que la fuerza es inversamente proporcional a la distancia entre dos objetos al cuadrado (F1/r 2) a una precisión de 1 parte en 1016. Nunca se han encontrado excepciones, incluso a las pequeñas distancias dentro del átomo.

    La ley de Coulomb se mantiene incluso dentro de los átomos, describiendo correctamente la fuerza entre el núcleo cargado positivamente y cada uno de los electrones cargados negativamente. Esta simple ley también explica correctamente las fuerzas que unen los átomos para formar moléculas y las fuerzas que unen átomos y moléculas para formar sólidos y líquidos.

    Generalmente, a medida que aumenta la distancia entre iones, la energía de atracción se acerca a cero y la unión iónica es menos favorable. A medida que aumenta la magnitud de las cargas opuestas, la energía aumenta y la unión iónica es más favorable.

    Un campo eléctrico es un campo vectorial que asocia a cada punto del espacio la fuerza Coulomb que experimentará una carga unitaria de prueba. Dado el campo eléctrico, la intensidad y dirección de una fuerza F sobre una cantidad de carga q en un campo eléctrico E está determinada por el campo eléctrico. Para una carga positiva, la dirección del campo eléctrico apunta a lo largo de líneas dirigidas radialmente lejos de la ubicación de la carga puntual, mientras que la dirección es hacia una carga negativa.

    Esta distribución alrededor de una molécula cargada es de naturaleza esférica y crea una especie de “nube” electrostática alrededor de la molécula. Las fuerzas de atracción o repulsión dentro de la distribución esférica de carga son más fuertes más cerca de la molécula, y se vuelven más débiles a medida que aumenta la distancia desde la molécula.

    Esta imagen muestra la nube externa de electrones de una molécula de agua neutra. La distribución de carga de la molécula de oxígeno es negativa y atrae a las dos moléculas de hidrógeno positivas. La atracción entre las dos cargas opuestas forma una molécula de agua neutra. Es una molécula polar porque todavía hay una separación de carga permanente porque los electrones pasan más tiempo cerca del oxígeno que los hidrógenos.

    Resolución de Problemas con Vectores y Ley de Coulomb

    La Ley de Coulomb, que calcula la fuerza eléctrica entre partículas cargadas, puede escribirse en notación vectorial como\(\mathrm { F } ( \mathrm { E } ) = \frac { \mathrm { kq } _ { 1 } \mathrm { q } _ { 2 } } { \mathrm { r } ^ { 2 } } \mathrm { r } +\).

    objetivos de aprendizaje

    • Explicar cuándo se puede usar la notación vectorial de la Ley de Coulomb

    Resolución de Problemas con Vectores y Ley de Coulomb

    Fuerza eléctrica entre cargas de dos puntos

    Para abordar las fuerzas electrostáticas entre las partículas cargadas eléctricamente, primero considere dos partículas con cargas eléctricas q y Q, separadas en el espacio vacío por una distancia r. Supongamos que queremos encontrar el vector de fuerza eléctrica en la carga q. (El vector de fuerza eléctrica tiene tanto una magnitud como una dirección.) Podemos expresar la ubicación de carga q como r q, y la ubicación de carga Q como r Q. De esta manera podemos saber tanto qué tan fuerte es la fuerza eléctrica sobre una carga, sino también en qué dirección se dirige esa fuerza. La Ley de Coulomb usando vectores se puede escribir como:

    \[\mathbf { F } _ { \mathbf { E } } = \dfrac { \operatorname { kq } Q \left( \mathrm { r } _ { \mathrm { q } } - \mathrm { r } _ { Q } \right) } { \left| \mathrm { r } _ { \mathrm { q } } - \mathrm { r } _ { Q } \right| ^ { 3 } }\]

    En esta ecuación, k es igual a\(\frac { 1 } { 4 \pi \varepsilon _ { 0 } \varepsilon }\), donde\(\varepsilon _ { 0 }\) está la permitividad del espacio libre y εε es la permitividad relativa del material en el que se sumergen las cargas. Las variables\(\mathbf { F} _ { \mathbf { E } } , \mathbf { \Gamma } _ { \mathrm { q } }\) y\(\mathbf{ R}_Q\) están en negrita porque son vectores. Por lo tanto, necesitamos encontrar\(\mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { Q } }\) mediante la realización de sustracción vectorial estándar. Esto significa que necesitamos restar los componentes correspondientes del vector\(\mathbf{r}_\mathrm{Q}}\) del vector\(\mathrmbf{r}_\mathrm{q}\).

    Esta notación vectorial se puede utilizar en el ejemplo simple de dos cargas puntuales donde solo una de las cuales es una fuente de carga.

    imagen

    Aplicación de la Ley de Coulomb: En un ejemplo sencillo, la notación vectorial de la Ley de Coulomb se puede utilizar cuando hay dos cargas puntuales y sólo una de las cuales es una carga fuente.

    Fuerza eléctrica en una carga de campo debido a cargas de fuente fija

    Supongamos que hay más de una carga fuente puntual proporcionando fuerzas sobre una carga de campo. diagramas un ejemplo bastante simple con tres cargas fuente (mostradas en verde e indexadas por subíndices) y una carga de campo (en rojo, designada q). Suponemos que las cargas de origen están fijas en el espacio, y la carga de campo q está sujeta a fuerzas de las cargas de origen.

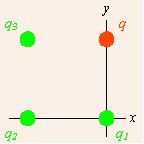
    imagen

    Cargos puntuales múltiples: La Ley de Coulomb se aplicaba a más de un cargo de fuente puntual que proporcionaba fuerzas en un cargo de campo.

    Anote el sistema de coordenadas que se ha elegido. Todas las cargas se encuentran en las esquinas de un cuadrado, y se elige el origen para colocarlas con la carga fuente inferior derecha, y alineadas con el cuadrado. Dado que solo podemos tener un origen de coordenadas, no más de uno de los puntos de origen puede estar en el origen, y los desplazamientos de diferentes puntos fuente al punto de campo difieren. La fuerza total sobre la carga de campo q se debe a aplicaciones de la fuerza descrita en la notación vectorial de la Ley de Coulomb de cada una de las cargas fuente. La fuerza total es, pues, la suma de estas fuerzas individuales.

    imagen

    Desplazamientos de carga de campo: Los desplazamientos de la carga de campo de cada carga fuente se muestran como flechas de color azul claro.

    Aplicar la Ley de Coulomb tres veces y sumar los resultados nos da:

    \[\mathbf { F } _ { \mathbf { E } _ { \mathbf { q } } } =\dfrac { \operatorname { kq } \cdot q _ { 1 } \left( \mathbf { r } _ { q } - \mathbf { r } _ { q 1 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 1 } \right| ^ { 3 } }+ \dfrac { \mathrm { kq } \cdot \mathbf { q } _ { 2 } \left( \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 2 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 2 } \right| ^ { 3 } }+ \dfrac { \mathrm { kq } \cdot \mathrm { q } _ { 3 } \left( \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 3 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 3 } \right| ^ { 3 } }\]

    Esta ecuación puede simplificarse aún más y aplicarse a un número fijo de puntos de carga.

    \[\mathbf { F } _ { \mathbf { n } } =\sum _ { i \neq n }\dfrac { q _ { n } q _ { i } \left( \mathbf { r } _ { n } - \mathbf { r } _ { i } \right) } { 4 \pi \epsilon _ { 0 } \left| \mathbf { r } _ { \mathrm { n } } - \mathbf { r } _ { \mathrm { i } } \right| ^ { 3 } }\]

    Ley de Coulomb: En este video continúo con mi serie de videos tutoriales sobre Electrostática. Está presentado a nivel de licenciatura y si bien está dirigido principalmente a carreras de física, debería ser útil para cualquiera que tome un primer curso de electricidad y magnetismo como ingenieros etc.

    Puntos Clave

    • El principio de superposición sugiere que la respuesta neta en un lugar y tiempo determinados causada por dos o más estímulos es la suma de las respuestas que habrían sido causadas por cada estímulo individualmente.
    • La fuerza total de Coulomb en una carga de prueba debida a un grupo de cargas es igual a la suma vectorial de todas las fuerzas de Coulomb entre la carga de prueba y otras cargas individuales.
    • La superposición de fuerzas no se limita a las fuerzas de Coulomb. Se aplica a cualquier tipo (o combinación) de fuerzas.
    • La fuerza entre dos objetos es inversamente proporcional al cuadrado de la distancia entre dos objetos.
    • Las fuerzas de atracción o repulsión dentro de la distribución esférica de carga son más fuertes más cercanas a la molécula y se vuelven más débiles a medida que aumenta la distancia desde la molécula.
    • Esta ley también explica las fuerzas que unen los átomos para formar moléculas y las fuerzas que unen átomos y moléculas para formar sólidos y líquidos.
    • La notación vectorial de la Ley de Coulomb se puede utilizar en el ejemplo simple de dos cargas puntuales donde solo una de las cuales es una fuente de carga.
    • La fuerza total en la carga de campo para cargas de múltiples fuentes puntuales es la suma de estas fuerzas individuales.
    • La Ley de Coulomb puede simplificarse aún más y aplicarse a un número fijo de puntos de carga.

    Elementos clave

    • Fuerza Lorentz: La fuerza ejercida sobre una partícula cargada en un campo electromagnético.
    • vector unitario: Un vector con longitud 1.
    • fuerza electrostática: La interacción electrostática entre partículas cargadas eléctricamente; la cantidad y dirección de atracción o repulsión entre dos cuerpos cargados.
    • ley del culombio: la ecuación matemática que calcula el vector de fuerza electrostática entre dos partículas cargadas

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 17.3: Ley de Coulomb is shared under a not declared license and was authored, remixed, and/or curated by Boundless.