Saltar al contenido principal
LibreTexts Español

23.2: Ondas electromagnéticas y sus propiedades

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128230

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Explicar el significado y la importancia de las ecuaciones de Maxwell

    Ecuaciones de Maxwell

    Las ecuaciones de Maxwell son un conjunto de cuatro ecuaciones diferenciales parciales que, junto con la ley de fuerza de Lorentz, forman la base de la electrodinámica clásica, la óptica clásica y los circuitos eléctricos.

    Nombradas en honor al estimado físico James Clerk Maxwell, las ecuaciones describen la creación y propagación de campos eléctricos y magnéticos. Fundamentalmente, describen cómo las cargas y corrientes eléctricas crean campos eléctricos y magnéticos, y cómo se afectan entre sí.

    Las ecuaciones de Maxwell se pueden dividir en dos subconjuntos principales. Los dos primeros, la ley de Gauss y la ley de Gauss para el magnetismo, describen cómo los campos emanan de cargas e imanes respectivamente. Los otros dos, la ley de Faraday y la ley de Ampere con la corrección de Maxwell, describen cómo circulan los campos eléctricos y magnéticos inducidos alrededor de sus respectivas fuentes.

    Cada una de las ecuaciones de Maxwell se puede observar desde la perspectiva “microscópica”, que trata sobre la carga total y la corriente total, y el conjunto “macroscópico”, que define dos nuevos campos auxiliares que permiten realizar cálculos sin conocer datos microscópicos como cargas de nivel atómico.

    Ley de Gauss

    La ley de Gauss relaciona un campo eléctrico con la carga o cargas que lo crean. El campo (E) apunta hacia cargas negativas y lejos de cargas positivas, y desde la perspectiva microscópica, está relacionado con la densidad de carga (ρ) y la permitividad de vacío (ε 0, o permitividad del espacio libre) como:

    \[\nabla \cdot \mathbf { E } = \dfrac { \rho } { \epsilon _ { 0 } }\]

    La Ley de Gauss básicamente dice que una cantidad neta de carga contenida dentro de una región del espacio generará un campo eléctrico que emana a través de la superficie que rodea esa región.

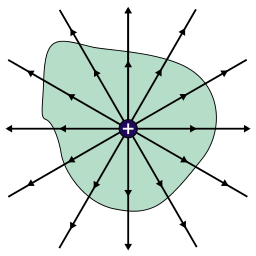
    imagen

    Ejemplo de la Ley de Gauss: Una carga positiva contenida dentro de una región del espacio crea un campo eléctrico que emana de la superficie de esa región.

    Ley de Gauss para el Magnetismo

    La ley de Gauss para el magnetismo establece que no hay “cargas magnéticas (o monopolos)” análogas a las cargas eléctricas, y que los campos magnéticos en cambio son generados por dipolos magnéticos. Dichos dipolos pueden representarse como bucles de corriente, pero en muchos sentidos son similares en apariencia a las “cargas magnéticas” positivas y negativas que son inseparables y por lo tanto no tienen una “carga magnética” neta formal.

    Las líneas de campo magnético forman bucles de tal manera que todas las líneas de campo que entran en un objeto lo dejan en algún momento. Así, el flujo magnético total a través de una superficie que rodea un dipolo magnético es siempre cero.

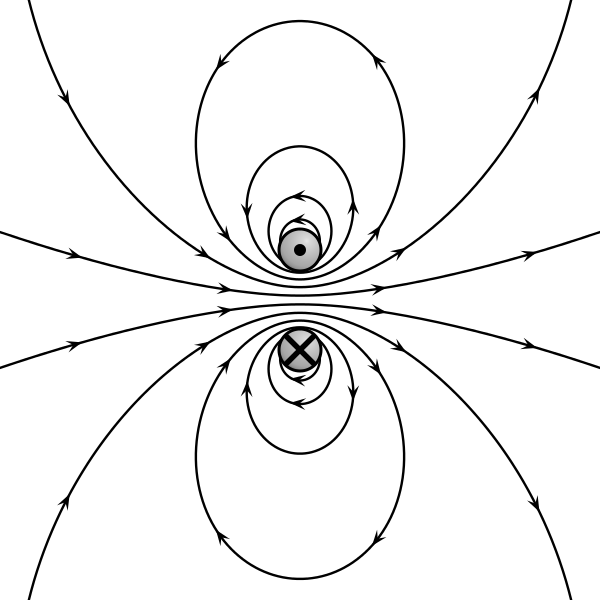
    imagen

    Líneas de campo provocadas por un dipolo magnético: Las líneas de campo creadas por este dipolo magnético forman bucles o se extienden infinitamente.

    La forma diferencial de la ley de Gauss para magnetismo magnético es

    \[\nabla \cdot \mathbf { B } = \mathbf { 0 }\]

    Ley de Faraday

    La ley de Faraday describe cómo un campo magnético variable en el tiempo (o flujo) induce un campo eléctrico. El principio detrás de este fenómeno se utiliza en muchos generadores eléctricos. Ambas ecuaciones diferenciales macroscópicas y microscópicas son las mismas, relacionando el campo eléctrico (E) con la derivada parcial de tiempo del campo magnético (B):

    \[\nabla \times \mathbf { E } = - \frac { \partial \mathbf { B } } { \partial \mathbf { t } }\]

    Ley Circuital de Ampere (con corrección de Maxwell)

    La ley de Ampere originalmente establecía que el campo magnético podría ser creado por corriente eléctrica. Maxwell agregó una segunda fuente de campos magnéticos en su corrección: un campo eléctrico cambiante (o flujo), que induciría un campo magnético incluso en ausencia de una corriente eléctrica. Nombró al campo eléctrico cambiante “corriente de desplazamiento”.

    La corrección de Maxwell muestra que las ondas electromagnéticas autosostenibles (luz) pueden viajar a través del espacio vacío incluso en ausencia de cargas o corrientes móviles, con el componente de campo eléctrico y el componente de campo magnético cada uno cambiando continuamente y cada uno perpetuando el otro.

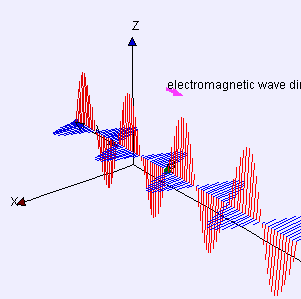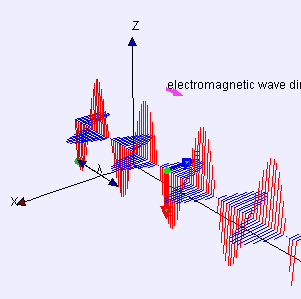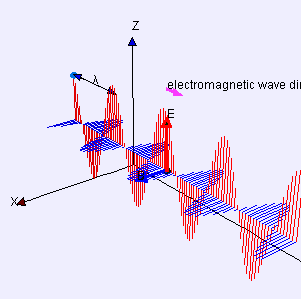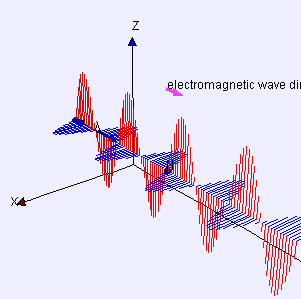
    imagen

    Ondas electromagnéticas: Las ondas eléctricas (rojas) y magnéticas (azules) se propagan en fase sinusoidalmente y perpendicularmente entre sí.

    El enfoque microscópico de la ley de amperios corregidos Maxwell relaciona el campo magnético (B) con la densidad de corriente (J, o corriente por unidad de área de sección transversal) y la derivada parcial de tiempo del campo eléctrico (E):

    \[\nabla \times \mathbf { B } = \mu _ { 0 } \mathbf { J } + \mu _ { 0 } \epsilon _ { 0 } \frac { \partial \mathbf { E } } { \partial t }\]

    La producción de ondas electromagnéticas

    Las ondas electromagnéticas son la combinación de ondas de campo eléctrico y magnético producidas por cargas móviles.

    objetivos de aprendizaje

    • Explicar el comportamiento autoperpetuante de una onda electromagnética

    Ondas electromagnéticas

    La radiación electromagnética, es una forma de energía emitida por partículas cargadas en movimiento. A medida que viaja por el espacio se comporta como una onda, y tiene un componente de campo eléctrico oscilante y un campo magnético oscilante. Estas ondas oscilan perpendicularmente y en fase entre sí.

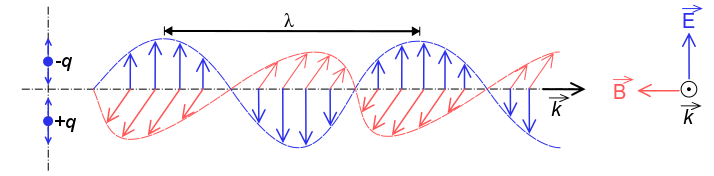
    imagen

    Onda electromagnética: Las ondas electromagnéticas son una onda transversal autopropagante de campos eléctricos y magnéticos oscilantes. La dirección del campo eléctrico se indica en azul, el campo magnético en rojo y la onda se propaga en la dirección x positiva. Observe que las ondas del campo eléctrico y magnético están en fase.

    La creación de todas las ondas electromagnéticas comienza con una partícula cargada. Esta partícula cargada crea un campo eléctrico (que puede ejercer una fuerza sobre otras partículas cargadas cercanas). Cuando acelera como parte de un movimiento oscilatorio, la partícula cargada crea ondas, u oscilaciones, en su campo eléctrico, y también produce un campo magnético (como lo predicen las ecuaciones de Maxwell).

    Una vez en movimiento, los campos eléctricos y magnéticos creados por una partícula cargada se autoperpetúan; los cambios dependientes del tiempo en un campo (eléctrico o magnético) producen el otro. Esto significa que un campo eléctrico que oscila en función del tiempo producirá un campo magnético, y un campo magnético que cambia en función del tiempo producirá un campo eléctrico. Tanto los campos eléctricos como los magnéticos en una onda electromagnética fluctuarán en el tiempo, uno haciendo que el otro cambie.

    Las ondas electromagnéticas son omnipresentes en la naturaleza (es decir, la luz) y se utilizan en la tecnología moderna: radio AM y FM, teléfonos inalámbricos y celulares, abridores de puertas de garaje, redes inalámbricas, radar, hornos de microondas, etc. Estos y muchos más dispositivos de este tipo utilizan ondas electromagnéticas para transmitir datos y señales.

    Todas las fuentes anteriores de ondas electromagnéticas utilizan el principio simple de carga móvil, que se puede modelar fácilmente. Colocar una moneda en contacto con ambos terminales de una batería de 9 voltios produce ondas electromagnéticas que se pueden detectar al llevar la antena de una radio (sintonizada a una estación productora de estática) a unas pocas pulgadas del punto de contacto.

    Energía y Momentum

    Las ondas electromagnéticas tienen energía e impulso que están ambos asociados con su longitud de onda y frecuencia.

    objetivos de aprendizaje

    • Relacionar la energía de una onda electromagnética con la frecuencia y la longitud de onda

    La radiación electromagnética puede describirse esencialmente como corrientes de fotones. Estos fotones se definen estrictamente como sin masa, pero tienen tanto energía como sorprendentemente, dada su falta de masa, impulso, que se puede calcular a partir de sus propiedades de onda.

    Las olas fueron poco entendidas hasta la década de 1900, cuando Max Planck y Albert Einstein desarrollaron correcciones modernas a la teoría clásica.

    Planck teorizó que los “cuerpos negros” (radiadores térmicos) y otras formas de radiación electromagnética no existían como espectros, sino en forma discreta, “cuantificada”. En otras palabras, solo había ciertas energías que una onda electromagnética podría tener. En su obra desarrolló lo que ahora se conoce como “la constante de Planck”, que es aproximadamente igual a 6.626×10 -34 J·s.

    Energía

    La energía (E) de un fotón puede estar relacionada con su frecuencia (f) por la constante de Planck (h):

    \[\mathrm { E } = \mathrm { hf } = \frac { \mathrm { hc } } { \lambda }\]

    La relación de velocidad de la luz (c) a la longitud de onda (λ) se puede sustituir en lugar de f para dar la misma ecuación a la energía en diferentes términos. Tenga en cuenta que la energía no puede tomar ningún valor: solo puede existir en incrementos de frecuencia multiplicados por la constante de Planck (o los tiempos constantes de Planck c divididos por la longitud de onda). Por lo tanto, la energía de una onda se “cuantifica”.

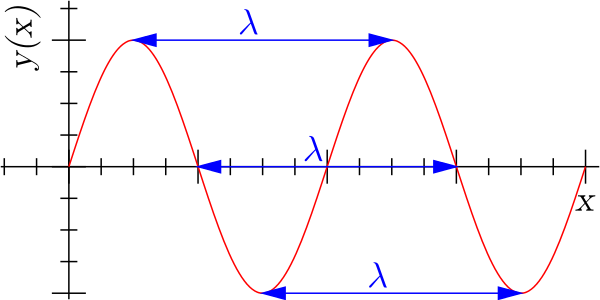
    imagen

    Longitud de onda: La longitud de onda de la función sinusoidal está representada por λ.

    Momentum

    El momento se define clásicamente como el producto de la masa y la velocidad y, por lo tanto, intuitivamente parecería irrelevante para una discusión sobre la radiación electromagnética, que es a la vez sin masa y compuesta por ondas.

    Sin embargo, Einstein demostró que la luz puede actuar como partículas en algunas circunstancias, y que existe una dualidad onda-partícula. Y, dado que relacionó energía y masa (e=mC2), se vuelve más concebible que una onda (que tiene un valor energético) no sólo tenga una ecuación a masa sino también un impulso.

    Y de hecho, Einstein demostró que el impulso (p) de un fotón es la relación entre su energía y la velocidad de la luz.

    \[\mathrm { p } = \dfrac { \mathrm { E } } { \mathrm { c } } = \dfrac { \mathrm { hf } } { \mathrm { c } } = \dfrac { \mathrm { h } } { \lambda }\]

    Sustituir E por hc/λ cancela los términos c, haciendo que el impulso también sea igual a la relación simple de la constante de Planck a la longitud de onda.

    La velocidad de la luz

    La velocidad de la luz en el vacío es una de las constantes más fundamentales en la física, desempeñando un papel fundamental en la física moderna.

    objetivos de aprendizaje

    • Relacionar la velocidad de la luz con el índice de refracción del medio

    La velocidad de la luz

    La velocidad de la luz es generalmente un punto de comparación para expresar que algo es rápido. muestra una representación a escala del tiempo que tarda un haz de luz en llegar a la luna desde la Tierra. Pero, ¿cuál es exactamente la velocidad de la luz?

    imagen

    Luz que va de la Tierra a la Luna: Se representa un haz de luz viajando entre la Tierra y la Luna en el tiempo que tarda un pulso de luz para moverse entre ellas: 1.255 segundos a su distancia orbital media (superficie-superficie). Los tamaños relativos y la separación del sistema Tierra-Luna se muestran a escala.

    Es solo eso: la velocidad de un fotón o partícula de luz. La velocidad de la luz en el vacío (comúnmente escrita como c) es de 299,792,458 metros por segundo. Esta es una constante física universal utilizada en muchas áreas de la física. Por ejemplo, podría estar familiarizado con la ecuación:

    \[\mathrm { E } = \mathrm { mc } ^ { 2 }\]

    donde E = Energía y m = masa. Esto se conoce como la equivalencia masa-energía, y utiliza la velocidad de la luz para interrelacionar el espacio y el tiempo. Esto no sólo explica la energía que contiene un cuerpo de masa, sino que también explica el obstáculo que tiene la masa sobre la velocidad.

    Hay muchos usos para la velocidad de la luz en un vacío, como en la relatividad especial, que dice que c es el límite de velocidad natural y nada puede moverse más rápido que él. Sin embargo, sabemos por nuestra comprensión de la física (y los átomos anteriores) que la velocidad a la que viaja algo también depende del medio por el que esté viajando. La velocidad a la que la luz se propaga a través de materiales transparentes (aire, vidrio, etc.) depende del índice de refracción de ese material, n:

    \[\mathrm { v } = \dfrac { \mathrm { c } } { \mathrm { n } }\]

    donde v = velocidad real de la luz que se mueve a través del medio, c = velocidad de la luz en vacío, y n = índice de refracción del medio. El índice de refracción del aire es de aproximadamente 1.0003, y a partir de esta ecuación podemos encontrar que la velocidad de la luz visible en el aire es de aproximadamente 90 km/s más lenta que c.

    Como se mencionó anteriormente, la velocidad de la luz (generalmente de la luz en el vacío) se utiliza en muchas áreas de la física. A continuación se muestra un ejemplo de una aplicación de la constante c.

    El Factor Lorentz

    Los objetos que se mueven rápidamente exhiben algunas propiedades contrarias a la intuición desde la perspectiva de la mecánica clásica. Por ejemplo, la longitud se contrae y el tiempo se dilata (corre más lento) para los objetos en movimiento. Los efectos suelen ser minuciosos, pero se notan a velocidades suficientemente altas. El factor Lorentz (γ) es el factor por el cual la longitud se acorta y el tiempo se dilata en función de la velocidad (v):

    \[\gamma = \left( 1 - \mathrm{ v } ^ { 2 } / \mathrm { c } ^ { 2 } \right) ^ { - 1 / 2 } \gamma = \left( 1 - \mathrm { v } ^ { 2 } / \mathrm { c } ^ { 2 } \right) ^ { - 1 / 2 } \gamma = \left( 1 - \mathrm { v } ^ { 2 } / \mathrm { c } ^ { 2 } \right) ^ { - 1 / 2 }\]

    A bajas velocidades, el cociente de v 2 /c 2 es suficientemente cercano a 0 de tal manera que γ es aproximadamente 1. Sin embargo, cuando la velocidad se acerca a c, γ aumenta rápidamente hacia el infinito.

    El efecto Doppler

    El Efecto Doppler es el cambio en la frecuencia percibida de una onda que resulta del movimiento de la fuente, el observador y el medio.

    objetivos de aprendizaje

    • Dar ejemplos de observaciones diarias del efecto Doppler

    El efecto Doppler

    El efecto Doppler es un cambio periódico en la frecuencia de un evento para un observador en movimiento en relación con la fuente del evento. Por lo general, este evento periódico es una ola.

    La mayoría de las personas han experimentado el efecto Doppler en acción. Considera un vehículo de emergencia en movimiento, haciendo sonar su sirena. A medida que se acerca a un observador, el tono del sonido (su frecuencia) suena más alto de lo que realmente es. Cuando el vehículo llega al observador, el tono se percibe como realmente es. Cuando el vehículo continúa lejos del observador, el tono se percibe como más bajo de lo que realmente es. Desde la perspectiva de un observador dentro del vehículo, el cabeceo de la sirena es constante.

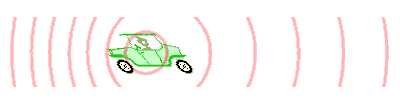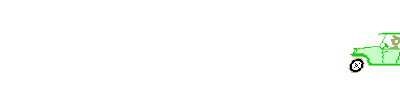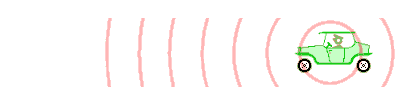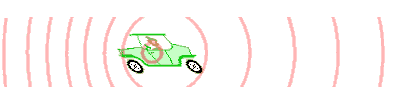
    imagen

    El efecto Doppler y las sirenas: ondas emitidas por una sirena en un vehículo en movimiento

    La diferencia en el tono percibido dependiendo de la ubicación del observador puede explicarse por el hecho de que la posición de la sirena cambia a medida que emite ondas. Una onda de sonido es emitida por un vehículo en movimiento cada milisegundo. El vehículo 'persigue' cada ola en una dirección. Para cuando se emite la siguiente onda, está más cerca (en relación con un espectador delante del vehículo) a la onda anterior de lo que sugeriría la frecuencia de la onda. En relación con un espectador detrás del vehículo, la segunda ola está más alejada de la primera de lo que cabría esperar, lo que sugiere una frecuencia más baja.

    El efecto Doppler puede ser causado por cualquier tipo de movimiento. En el ejemplo anterior, la sirena se movió con relación a un observador estacionario. Si el observador se mueve con relación a la sirena estacionaria, el observador notará el efecto Doppler en el tono de la sirena. Por último, si se mueve el medio por el que se propagan las ondas, el efecto Doppler se notará incluso para un observador estacionario. Un ejemplo de este fenómeno es el viento.

    Cuantitativamente, el efecto Doppler se puede caracterizar relacionando la frecuencia percibida (f) con la velocidad de las ondas en el medio (c), la velocidad del receptor con respecto al medio (v r), la velocidad de la fuente relativa al medio (v s) y la frecuencia emitida real (f 0):

    \[\mathrm { f } = \left( \dfrac { \mathrm { c } + \mathrm { v } _ { \mathrm { r } } } { \mathrm { c } + \mathrm { v } _ { \mathrm { s } } } \right) \mathrm { f } _ { 0 }\]

    imagen

    El efecto Doppler: cambio de longitud de onda debido al movimiento de la fuente

    Transferencia de Momentum y Presión de Radiación

    La presión de radiación es la presión ejercida sobre cualquier superficie expuesta a radiación electromagnética (EM).

    objetivos de aprendizaje

    • Explicar la formación de la presión de radiación

    La presión de radiación es la presión ejercida sobre cualquier superficie expuesta a radiación electromagnética (EM). La radiación EM (o fotón, que es un cuántico de luz) lleva impulso; este impulso se transfiere a un objeto cuando la radiación es absorbida o reflejada. Quizás uno de los ejemplos más conocidos de la presión de radiación serían las colas de cometa. El cometa de Haley se muestra en.

    imagen

    Halley's Comet: A medida que un cometa se acerca al Sistema Solar interno, la radiación solar hace que los materiales volátiles dentro del cometa se vaporicen y salgan del núcleo. Las corrientes de polvo y gas así liberadas forman una atmósfera alrededor del cometa (llamada coma), y la fuerza ejercida sobre el coma por la presión de radiación del Sol y el viento solar provocan la formación de una enorme cola que apunta lejos del Sol.

    Aunque la presión de radiación se puede entender usando la electrodinámica clásica, aquí examinaremos el argumento mecánico cuántico. Desde la perspectiva de la teoría cuántica, la luz está hecha de fotones: partículas con masa cero pero que transportan energía y —lo que es más importante en este argumento— impulso. Según relatividad especial, debido a que los fotones carecen de masa, su energía (E) y su impulso (p) están relacionados por E=pc.

    Consideremos ahora un haz de luz perpendicularmente incidente sobre una superficie, y supongamos que el haz de luz es totalmente absorbido. El impulso que llevan los fotones es una cantidad conservada (es decir, no se puede destruir) por lo que debe transferirse a la superficie; así la absorción del haz de luz hace que la superficie gane impulso. La Segunda Ley de Newton nos dice que la fuerza es igual a la tasa de cambio de impulso; así, durante cada segundo, la superficie experimenta una fuerza (o presión, ya que la presión es fuerza por unidad de área) debido al impulso que los fotones le transfieren.

    Esto nos da: presión = impulso transferido por segundo por unidad de área = energía depositada por segundo por unidad de área/c = I/c, (donde I es la intensidad del haz de luz).

    Enfriamiento por Láser

    Hay muchas variaciones de enfriamiento por láser, pero todas utilizan la presión de radiación para eliminar la energía de los gases atómicos (y por lo tanto enfriar la muestra). En el enfriamiento láser (a veces llamado enfriamiento Doppler), la frecuencia de la luz se sintoniza ligeramente por debajo de una transición electrónica en el átomo. Debido a que la luz se desafina al “rojo” (es decir, a menor frecuencia) de la transición, los átomos absorberán más fotones si se mueven hacia la fuente de luz, debido al efecto Doppler. Por lo tanto, si se aplica luz desde dos direcciones opuestas, los átomos siempre dispersarán más fotones del rayo láser apuntando opuesto a su dirección de movimiento (configuraciones típicas aplican tres pares opuestos de rayos láser como en).

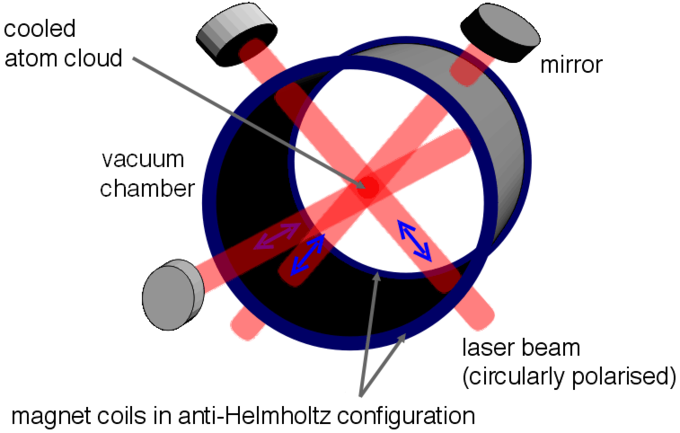
    imagen

    La trampa magnética óptica: configuración experimental de trampa magnética óptica (MOT), que utiliza presión de radiación para enfriar especies atómicas. Los átomos se ralentizan al absorber (y emitir) fotones.

    En cada evento de dispersión, el átomo pierde un impulso igual al impulso del fotón. Si el átomo (que ahora se encuentra en el estado excitado) entonces emite un fotón espontáneamente, será pateado por la misma cantidad de impulso, solo en una dirección aleatoria. Dado que la pérdida de impulso inicial fue opuesta a la dirección del movimiento (mientras que la ganancia de impulso posterior fue en una dirección aleatoria), el resultado general del proceso de absorción y emisión es reducir la velocidad del átomo. Si la absorción y emisión se repiten muchas veces, se reducirá la velocidad promedio (y por lo tanto la energía cinética) del átomo. Dado que la temperatura de un grupo de átomos es una medida de la energía cinética interna aleatoria promedio, esto equivale a enfriar los átomos. Las configuraciones simples de enfriamiento por láser pueden producir una muestra fría de gases atómicos a alrededor de 1mK (=10 -3 K) a partir de un gas a temperatura ambiente.

    Puntos Clave

    • Las cuatro ecuaciones de Maxwell describen cómo las cargas y corrientes eléctricas crean campos eléctricos y magnéticos, y cómo se afectan entre sí.
    • La ley de Gauss relaciona un campo eléctrico con la carga o cargas que lo crean.
    • La ley de Gauss para el magnetismo establece que no hay “cargas magnéticas” análogas a las cargas eléctricas, y que los campos magnéticos en cambio son generados por dipolos magnéticos.
    • La ley de Faraday describe cómo un campo magnético variable en el tiempo (o flujo) induce un campo eléctrico. El principio detrás de este fenómeno se utiliza en muchos generadores eléctricos.
    • La ley de Ampere establecía originalmente que un campo magnético es creado por una corriente eléctrica. Maxwell agregó que un flujo eléctrico cambiante también puede generar un campo magnético.
    • Las ondas electromagnéticas consisten en ondas de campo eléctrico y magnético. Estas ondas oscilan en planos perpendiculares entre sí, y están en fase.
    • La creación de todas las ondas electromagnéticas comienza con una partícula cargada oscilante, que crea campos eléctricos y magnéticos oscilantes.
    • Una vez en movimiento, los campos eléctricos y magnéticos que crea una partícula cargada se autoperpetúan: los cambios dependientes del tiempo en un campo (eléctrico o magnético) producen el otro.
    • Max Planck demostró que la energía de un fotón (una corriente del cual es una onda electromagnética) se cuantifica y puede existir en múltiplos de la “constante de Planck” (denotada como h, aproximadamente igual a 6.626×10 -34 J·s).
    • \(\mathrm { E } = \mathrm { hf } = \frac { \mathrm { hc } } { \lambda } \)describe la energía (E) de un fotón en función de la frecuencia (f), o longitud de onda (λ).
    • \(\mathrm { p } = \frac { \mathrm { E } } { \mathrm { c } } = \frac { \mathrm { hf } } { \mathrm { c } } = \frac { \mathrm { h } } { \lambda }\)describe el momento (p) de un fotón en función de su energía, frecuencia o longitud de onda.
    • El valor máximo posible para la velocidad de la luz es el de la luz en un vacío, y esta velocidad se utiliza para una constante en muchas áreas de la física.
    • c es el símbolo utilizado para representar la velocidad de la luz en un vacío, y su valor es de 299,792,458 metros por segundo.
    • Cuando la luz viaja a través del medio, su velocidad se ve obstaculizada por el índice de refracción de ese medio. Su velocidad real se puede encontrar con:\(v=\frac{c}{n}\).
    • El efecto Doppler se observa muy comúnmente en acción.
    • El efecto Doppler se puede observar en el cambio aparente en el tono de una sirena en un vehículo de emergencia, según un observador estacionario.
    • El observador notará el efecto Doppler en el tono de la sirena estacionaria cuando se mueva con relación a su tono, o si el medio se mueve cuando el observador está estacionario.
    • Los fotones llevan impulso (p = E/c). Cuando los fotones son absorbidos o reflejados en una superficie, la superficie recibe patadas de impulso. Esta transferencia de impulso conduce a la presión de radiación.
    • La radiación electromagnética aplica una presión de radiación igual a la Intensidad (del haz de luz) dividida por c (velocidad de la luz).
    • El enfriamiento por láser utiliza presión de radiación para eliminar la energía de los gases atómicos. La técnica puede producir muestras frías de gases a 1mK más o menos.

    Términos Clave

    • ecuación diferencial: Ecuación que involucra las derivadas de una función.
    • flujo: Una descripción cuantitativa de la transferencia de una cantidad de vector dada a través de una superficie. En este contexto, nos referimos al flujo eléctrico y al flujo magnético.
    • Onda electromagnética: Una onda de campos eléctricos y magnéticos oscilantes.
    • fase: Se dice que las olas están “en fase” cuando comienzan en la misma parte (e.g., cresta) de sus respectivos ciclos.
    • fotón: La cuántica de la luz y otra energía electromagnética, considerada como una partícula discreta que tiene masa de reposo cero, sin carga eléctrica, y una vida útil indefinidamente larga.
    • longitud de onda: La longitud de un solo ciclo de una onda, medida por la distancia entre un pico o canal de una onda y el siguiente; a menudo se designa en física como λ, y corresponde a la velocidad de la onda dividida por su frecuencia.
    • frecuencia: El cociente del número de veces n un fenómeno periódico se produce a lo largo del tiempo t en que ocurre: f = n/t.
    • relatividad especial: Una teoría que (descuidando los efectos de la gravedad) reconcilia el principio de relatividad con la observación de que la velocidad de la luz es constante en todos los marcos de referencia.
    • índice de refracción: La relación de la velocidad de la luz en el aire o vacío a la de otro medio.
    • Efecto Doppler: Cambio aparente en la frecuencia de una onda cuando el observador y la fuente de la onda se mueven uno con relación al otro.
    • electrodinámica clásica: Una rama de la física teórica que estudia las consecuencias de las fuerzas electromagnéticas entre cargas eléctricas y corrientes.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    23.2: Ondas electromagnéticas y sus propiedades is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.