Saltar al contenido principal
LibreTexts Español

3.1: Movimiento en Dos Dimensiones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128437
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Velocidad constante

    Un objeto que se mueve con velocidad constante debe tener una velocidad constante en una dirección constante.

    objetivos de aprendizaje

    • Examinar los términos de velocidad constante y cómo se aplican a la aceleración

    El movimiento con velocidad constante es una de las formas de movimiento más simples. Este tipo de movimiento ocurre cuando un objeto se está moviendo (o deslizando) en presencia de poca o insignificante fricción, similar a la de un disco de hockey que se desliza sobre el hielo. Para tener una velocidad constante, un objeto debe tener una velocidad constante en una dirección constante. La dirección constante limita el movimiento del objeto a una trayectoria recta.

    La segunda ley de Newton (\(\mathrm{F=ma}\)) sugiere que cuando se aplica una fuerza a un objeto, el objeto experimentaría aceleración. Si la aceleración es 0, el objeto no debería tener ninguna fuerza externa aplicada sobre él. Matemáticamente, esto se puede mostrar de la siguiente manera:

    \[\mathrm{a=\frac{dv}{dt}=0 ⇒ v=const.}\]

    Si un objeto se mueve a velocidad constante, la gráfica de distancia vs. tiempo (\(\mathrm{x}\)vs.\(\mathrm{t}\)) muestra el mismo cambio de posición en cada intervalo de tiempo. Por lo tanto, el movimiento de un objeto a velocidad constante está representado por una línea recta:\(\mathrm{x=x_0+vt}\), donde\(\mathrm{x_0}\) está el desplazamiento cuando\(\mathrm{t=0}\) (o en la intercepción del eje y).

    imagen

    Movimiento con Velocidad Constante: Cuando un objeto se mueve con velocidad constante, no cambia de dirección ni velocidad y por lo tanto se representa como una línea recta cuando se grafica como distancia a lo largo del tiempo.

    También puedes obtener la velocidad de un objeto si conoces su rastro a lo largo del tiempo. Dado un gráfico como en, podemos calcular la velocidad a partir del cambio en la distancia sobre el cambio en el tiempo. En términos gráficos, la velocidad puede interpretarse como la pendiente de la línea. La velocidad puede ser positiva o negativa, y está indicada por el signo de nuestra pendiente. Esto nos dice en qué dirección se mueve el objeto.

    Aceleración constante

    El análisis del movimiento bidimensional del proyectil se realiza dividiéndolo en dos movimientos: a lo largo de los ejes horizontal y vertical.

    objetivos de aprendizaje

    • Analizar el movimiento de un proyectil bidimensional a lo largo de ejes horizontales y verticales

    El movimiento del proyectil es el movimiento de un objeto lanzado, o proyectado, al aire, sujeto únicamente a la fuerza de la gravedad. El objeto se llama proyectil, y su trayectoria se llama trayectoria. El movimiento de los objetos que caen es un simple tipo unidimensional de movimiento de proyectil en el que no hay movimiento horizontal. En el movimiento bidimensional del proyectil, como el de un balón de fútbol u otro objeto lanzado, hay tanto una componente vertical como una horizontal al movimiento.

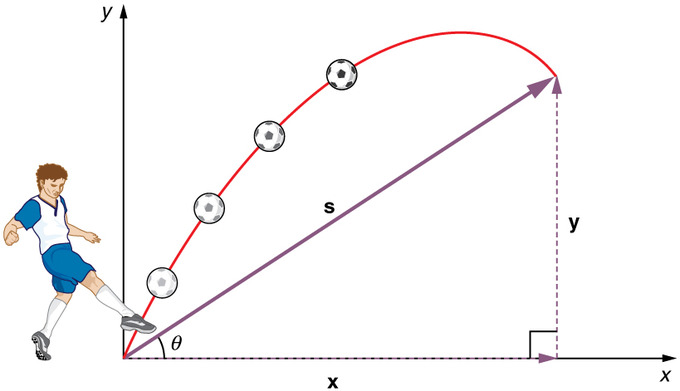
    imagen

    Movimiento del proyectil: Lanzar una roca o patear una pelota generalmente produce un patrón de movimiento de proyectil que tiene tanto una componente vertical como una horizontal.

    El dato más importante a recordar es que el movimiento a lo largo de ejes perpendiculares son independientes y por lo tanto se pueden analizar por separado. La clave para analizar el movimiento bidimensional del proyectil es dividirlo en dos movimientos, uno a lo largo del eje horizontal y otro a lo largo del vertical. Para describir el movimiento debemos tratar con la velocidad y la aceleración, así como con el desplazamiento.

    Asumiremos que todas las fuerzas excepto la gravedad (como la resistencia al aire y la fricción, por ejemplo) son despreciables. Los componentes de la aceleración son entonces muy simples:\(\mathrm{a_y=−g=−9.81\frac{m}{s^2}}\) (suponemos que el movimiento ocurre a alturas suficientemente pequeñas cerca de la superficie de la tierra para que la aceleración debida a la gravedad sea constante). Debido a que la aceleración debida a la gravedad es a lo largo de la dirección vertical solamente,\(\mathrm{a_x=0}\). Así, las ecuaciones cinemáticas que describen el movimiento a lo largo de las\(\mathrm{y}\) direcciones\(\mathrm{x}\) y respectivamente, se pueden utilizar:

    \[\begin{align} \mathrm{x} & \mathrm{=x_0+v_xt} \\ \mathrm{y} & \mathrm{=v_{0y}+a_yt} \\ \mathrm{y} & \mathrm{=y_0+v_{0y}t+\dfrac{1}{2}a_yt^2} \\ \mathrm{v_y^2} &\mathrm{=v_{0y}^2+2a_y(y−y_0)} \end{align}\]

    Analizamos el movimiento bidimensional del proyectil dividiéndolo en dos movimientos unidimensionales independientes a lo largo de los ejes vertical y horizontal. El movimiento horizontal es simple, porque\(\mathrm{a_x=0}\) y por lo tanto\(\mathrm{v_x}\) es constante. La velocidad en dirección vertical comienza a disminuir a medida que un objeto se eleva; en su punto más alto, la velocidad vertical es cero. A medida que un objeto vuelve a caer hacia la Tierra, la velocidad vertical vuelve a aumentar en magnitud pero apunta en dirección opuesta a la velocidad vertical inicial. Los movimientos xx e yy se pueden recombinar para dar la velocidad total en cualquier punto dado de la trayectoria.

    Puntos Clave

    • Velocidad constante significa que el objeto en movimiento se mueve en línea recta a una velocidad constante.
    • Esta línea se puede representar algebraicamente como:\(\mathrm{x=x_0+vt}\), donde\(\mathrm{x_0}\) representa la posición del objeto en\(\mathrm{t=0}\), y la pendiente de la línea indica la velocidad del objeto.
    • La velocidad puede ser positiva o negativa, y está indicada por el signo de nuestra pendiente. Esto nos dice en qué dirección se mueve el objeto.
    • La aceleración constante en movimiento en dos dimensiones generalmente sigue un patrón de proyectil.
    • El movimiento del proyectil es el movimiento de un objeto lanzado o proyectado al aire, sujeto solo a la aceleración (vertical) debida a la gravedad.
    • Analizamos el movimiento bidimensional del proyectil dividiéndolo en dos movimientos unidimensionales independientes a lo largo de los ejes vertical y horizontal.

    Términos Clave

    • velocidad constante: Movimiento que no cambia en velocidad ni dirección.
    • cinemática: de o relacionada con el movimiento o la cinemática

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 3.1: Movimiento en Dos Dimensiones is shared under a not declared license and was authored, remixed, and/or curated by Boundless.