Saltar al contenido principal
LibreTexts Español

5.1: Introducción a la UCM y Gravitación

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128552

    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    Cinemática de la UCM

    El movimiento circular uniforme es un movimiento en una trayectoria circular a velocidad constante.

    objetivos de aprendizaje

    • Relacionar la fuerza centrípeta y la aceleración centrípeta con el movimiento circular uniforme

    Cantidades angulares

    Bajo un movimiento circular uniforme, las cantidades angulares y lineales tienen relaciones simples. Cuando los objetos giran alrededor de algún eje, cada punto del objeto sigue un arco circular. El ángulo de rotación es la cantidad de rotación y es análogo a la distancia lineal. Definimos el ángulo de rotación\(\mathrm{Δθ}\) para que sea la relación entre la longitud del arco y el radio de curvatura:

    \[\mathrm{Δθ=\dfrac{Δs}{r}}\]

    imagen

    Ángulo θθ y longitud de arco ss: El radio de un círculo se gira a través de un ángulo\(\mathrm{Δθ}\). La longitud del arco\(\mathrm{Δs}\) se describe en la circunferencia.

    Definimos la velocidad angular ωω como la velocidad de cambio de un ángulo. En símbolos, esto es\(\mathrm{ω=\frac{Δθ}{Δt}}\), donde se\(\mathrm{Δθ}\) produce una rotación angular en un tiempo\(\mathrm{Δt}\). De la relación de\(\mathrm{s}\) y (\(\mathrm{Δs=rΔθ}\)), vemos:

    \[\mathrm{v=\dfrac{Δs}{Δt}=r\dfrac{Δθ}{Δt}=rω}\]

    Bajo un movimiento circular uniforme, la velocidad angular es constante. La aceleración se puede escribir como:

    \[\mathrm{ac=\dfrac{dv}{dt}=ω\dfrac{dr}{dt}=ωv=rω^2=\dfrac{v^2}{r}}\]

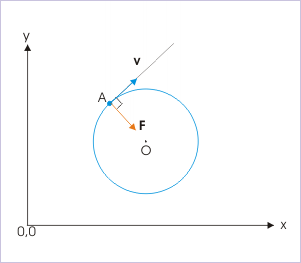
    Esta aceleración, responsable del movimiento circular uniforme, se llama aceleración centrípeta.

    Fuerza centrípeta

    Cualquier fuerza o combinación de fuerzas puede provocar una aceleración centrípeta o radial. Solo algunos ejemplos son la tensión en la cuerda sobre una bola de atadura, la fuerza de la gravedad de la Tierra sobre la Luna, la fricción entre los patines y el piso de una pista, la fuerza de una calzada inclinada sobre un automóvil y las fuerzas en el tubo de una centrífuga giratoria.

    Cualquier fuerza neta que cause un movimiento circular uniforme se denomina fuerza centrípeta. La dirección de una fuerza centrípeta es hacia el centro de curvatura, la misma que la dirección de la aceleración centrípeta. Según la segunda ley de movimiento de Newton, la fuerza neta es la aceleración por masa. Para un movimiento circular uniforme, la aceleración es la aceleración centrípeta:\(\mathrm{a=a_c}\). Así, la magnitud de la fuerza centrípeta\(\mathrm{F_c}\) es:

    \[\mathrm{F_c=ma_c=m\frac{v^2}{r}=mrω^2}\]

    Dinámica de la UCM

    La ley universal de la gravitación de Newton establece que cada partícula atrae a todas las demás partículas con una fuerza a lo largo de una línea que las une.

    objetivos de aprendizaje

    • Relacionar las leyes de Kepler con la ley universal de la gravitación de Newton

    Ley Universal de Gravitación de Newton

    La ley universal de la gravitación de Newton establece que cada partícula en el universo atrae a todas las demás partículas con una fuerza a lo largo de una línea que las une. La fuerza es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellas. Para dos cuerpos que tienen masas mm y MM con una distancia rr entre sus centros de masa, la ecuación para la ley universal de gravitación de Newton es:

    \[\mathrm{F=G\dfrac{mM}{r^2}}\]

    La fuerza gravitacional es la responsable de que los satélites artificiales orbiten la Tierra. La órbita de la Luna alrededor de la Tierra, las órbitas de planetas, asteroides, meteoros y cometas alrededor del Sol son otros ejemplos de órbitas gravitacionales. Históricamente, Kepler descubrió sus 3 leyes (llamadas la ley del movimiento planetario de Kepler) mucho antes de los días de Newton. Kepler ideó sus leyes después de un cuidadoso estudio (a lo largo de unos 20 años) de una gran cantidad de observaciones meticulosamente registradas del movimiento planetario realizadas por Tycho Brahe (1546—1601).

    Leyes de Kepler

    • La órbita de cada planeta alrededor del Sol es una elipse con el Sol en un foco.
    • Cada planeta se mueve para que una línea imaginaria trazada desde el Sol hasta el planeta barre áreas iguales en tiempos iguales.
    • La proporción de los cuadrados de los períodos de dos planetas cualesquiera alrededor del Sol es igual a la proporción de los cubos de sus distancias promedio del Sol.

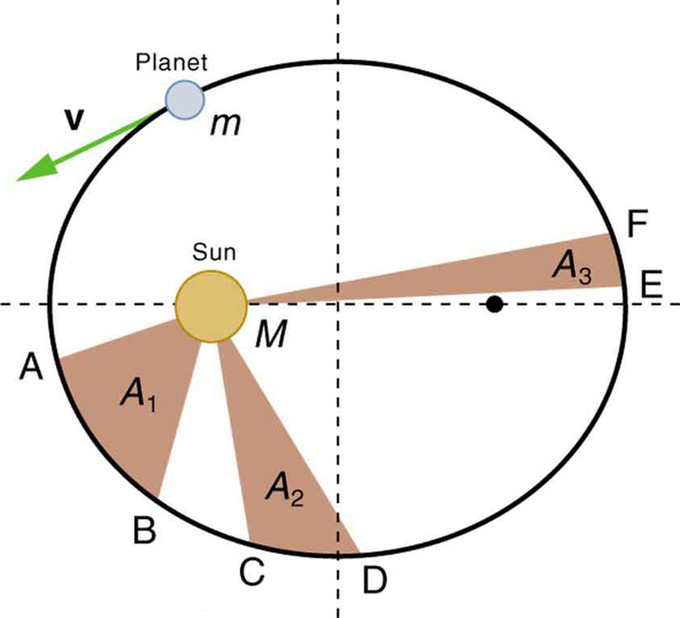
    imagen

    Segunda Ley de Kepler: Las regiones sombreadas tienen áreas iguales. Se necesitan tiempos iguales para que mm pase de\(\mathrm{A}\) a\(\mathrm{B}\), de\(\mathrm{C}\) a\(\mathrm{D}\), y de\(\mathrm{E}\) a\(\mathrm{F}\). La masa mm se mueve más rápido cuando está más cerca de\(\mathrm{M}\). La segunda ley de Kepler fue ideada originalmente para planetas que orbitan el Sol, pero tiene una validez más amplia.

    imagen

    Elipses y Primera Ley de Kepler: (a) Una elipse es una curva cerrada tal que la suma de las distancias desde un punto en la curva a los dos focos (\(\mathrm{f_1}\)y\(\mathrm{f_2}\)) es una constante. Puedes dibujar una elipse como se muestra poniendo un alfiler en cada foco, y luego colocando una cuerda alrededor de un lápiz y los alfileres y trazando una línea en papel. Un círculo es un caso especial de una elipse en la que coinciden los dos focos (así cualquier punto del círculo está a la misma distancia del centro). b) Para cualquier órbita gravitacional cerrada,\(\mathrm{m}\) sigue una trayectoria elíptica con\(\mathrm{M}\) un foco. La primera ley de Kepler establece este hecho para los planetas que orbitan el Sol.

    Derivación de la Tercera Ley de Kepler para Órbitas Circulares

    La tercera ley de Kepler es equivalente a:

    \[\mathrm{\dfrac{T^2_1}{T^2_2}=\dfrac{r^1_3}{r^2_3}}\]

    \(\mathrm{T}\)es el periodo (tiempo para una órbita) y\(\mathrm{r}\) es el radio promedio. Derivaremos la tercera ley de Kepler, comenzando por las leyes del movimiento de Newton y su ley universal de la gravitación. Asumiremos una trayectoria circular (no elíptica) por simplicidad.

    Consideremos una órbita circular de una pequeña masa mm alrededor de una gran masa\(\mathrm{M}\), satisfaciendo las dos condiciones señaladas al inicio de esta sección. La gravedad suministra la fuerza centrípeta a la masa\(\mathrm{m}\). Por lo tanto, para un movimiento circular uniforme:

    \[\mathrm{G\dfrac{mM}{r^2}=ma_c=m\dfrac{v^2}{r}}\]

    La masa se\(\mathrm{m}\) cancela, rindiendo:

    \[\mathrm{G\dfrac{mM}{r^2}=v^2}\]

    Ahora, para llegar a la tercera ley de Kepler, debemos meter el punto\(\mathrm{T}\) en la ecuación. Por definición, periodo\(\mathrm{T}\) es el tiempo para una órbita completa. Ahora la velocidad promedio\(\mathrm{v}\) es la circunferencia dividida por el periodo:

    \[\mathrm{v=\dfrac{2πr}{T}}\]

    Sustituyendo esto en la ecuación anterior da:

    \[\mathrm{G\dfrac{M}{r}=\dfrac{4π^2r^2}{T^2}}\]

    Resolviendo para\(\mathrm{T^2}\) rendimientos:

    \[\mathrm{T^2=\dfrac{4π^2}{GM}r^3}\]

    Ya que\(\mathrm{T^2}\) es proporcional a\(\mathrm{r^3}\), su relación es constante. Esta es la tercera ley de Kepler.

    Curvas de Autopista Bancadas y Sin Respaldo

    En una “curva idealmente inclinada”, el ángulo\(\mathrm{θ}\) se elige de tal manera que se puede negociar la curva a cierta velocidad sin la ayuda de la fricción.

    objetivos de aprendizaje

    • Derivar\(\mathrm{θ}\) para una curva idealmente bancada para la velocidad

    Visión general

    Como ejemplo de un movimiento circular uniforme y su aplicación, consideremos ahora las curvas inclinadas, donde la pendiente de la carretera te ayuda a negociar la curva. Cuanto mayor sea el ángulo\(\mathrm{θ}\), más rápido podrás tomar la curva. Las pistas de carreras para bicicletas así como los autos, por ejemplo, suelen tener curvas pronunciadas. En una “curva idealmente inclinada”, el ángulo\(\mathrm{θ}\) es tal que se puede negociar la curva a cierta velocidad sin la ayuda de la fricción entre las llantas y la carretera. Derivaremos una expresión\(\mathrm{θ}\) para una curva idealmente bancada para la velocidad\(\mathrm{v}\) y consideraremos un ejemplo relacionado con ella.

    Movimiento Circular Uniforme y Determinación de Condiciones Bancarias Ideales

    Para la banca ideal, la fuerza externa neta es igual a la fuerza centrípeta horizontal en ausencia de fricción. Los componentes de la fuerza normal\(\mathrm{N}\) en las direcciones horizontal y vertical deben ser iguales a la fuerza centrípeta y al peso del automóvil, respectivamente. En los casos en que las fuerzas no son paralelas, lo más conveniente es considerar componentes a lo largo de ejes perpendiculares, en este caso, las direcciones vertical y horizontal.

    imagen

    Auto en una curva bancada: El auto en esta curva bancada se aleja y gira a la izquierda.

    Arriba hay un diagrama de carrocería libre para un automóvil en una curva bancada sin fricción. Las únicas dos fuerzas externas que actúan sobre el automóvil son su peso ww y la fuerza normal de la carretera\(\mathrm{N}\). (Una superficie sin fricción solo puede ejercer una fuerza perpendicular a la superficie, es decir, una fuerza normal) Estas dos fuerzas deben agregarse para dar una fuerza externa neta que es horizontal hacia el centro de curvatura y tiene magnitud\(\mathrm{\frac{mv^2}{r}}\). Solo la fuerza normal tiene un componente horizontal, por lo que esta debe ser igual a la fuerza centrípeta, es decir:

    \[\mathrm{N \sin ⁡θ=\dfrac{mv^2}{r}}\]

    Debido a que el automóvil no sale de la superficie de la carretera, la fuerza vertical neta debe ser cero, lo que significa que los componentes verticales de las dos fuerzas externas deben ser iguales en magnitud y opuestos en dirección. De la figura, vemos que el componente vertical de la fuerza normal es\(\mathrm{N \cos ⁡θ}\), y la única otra fuerza vertical es el peso del automóvil. Estos deben ser iguales en magnitud, así:

    \[\mathrm{N \cos θ=mg}\]

    Dividiendo las ecuaciones anteriores rinde:

    \[\mathrm{ \tan θ=\dfrac{v^2}{rg}}\]

    Tomando la tangente inversa da:

    \[\mathrm{θ=\tan ^{−1}(\dfrac{v^2}{rg})}\]

    para una curva idealmente bancada sin fricción.

    Esta expresión se puede entender considerando cómo\(\mathrm{θ}\) depende de\(\mathrm{v}\) y\(\mathrm{r}\). Se\(\mathrm{θ}\) obtendrá una grande para una grande\(\mathrm{v}\) y una pequeña\(\mathrm{r}\). Es decir, las carreteras deben estar inclinadas para altas velocidades y curvas pronunciadas. La fricción ayuda, ya que le permite tomar la curva a mayor o menor velocidad que si la curva es sin fricción. Tenga en cuenta que\(\mathrm{θ}\) no depende de la masa del vehículo.

    Puntos Clave

    • Bajo un movimiento circular uniforme, las cantidades angulares y lineales tienen relaciones simples. La longitud de un arco es proporcional al ángulo de rotación y al radio. También,\(\mathrm{v=rω}\).
    • La aceleración responsable del movimiento circular uniforme se llama aceleración centrípeta. Se da como\(\mathrm{a_c=rω^2=\frac{v^2}{r}}\).
    • Cualquier fuerza neta que cause un movimiento circular uniforme se denomina fuerza centrípeta. La dirección de una fuerza centrípeta es hacia el centro de curvatura y su magnitud es\(\mathrm{m\frac{v^2}{r}=mrω^2}\).
    • La fuerza gravitacional es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellas.
    • Kepler descubrió leyes que describían el movimiento planetario mucho antes de los días de Newton, basadas puramente en las observaciones de Tycho Brahe.
    • Las leyes de Kepler pueden derivarse de la ley universal de gravitación de Newton y su ecuación de movimiento.
    • Para la banca ideal, la fuerza externa neta es igual a la fuerza centrípeta horizontal en ausencia de fricción.
    • Para la banca ideal, los componentes de la fuerza normal NN en las direcciones horizontal y vertical deben ser iguales a la fuerza centrípeta y al peso del automóvil, respectivamente.
    • La condición bancaria ideal se da como\(\mathrm{θ=\tan ^{−1}⁡(\frac{v^2}{rg})}\).

    Términos Clave

    • centrípeta: Dirigido o moviéndose hacia un centro.
    • asteroide: Un objeto sólido natural, que es más pequeño que un planeta y no es un cometa, que orbita una estrella.
    • planeta: Un cuerpo grande que orbita directamente cualquier estrella (o cúmulo estelar) pero que no ha alcanzado la fusión nuclear.
    • fuerza normal: Cualquier fuerza que actúe normal, a una superficie o perpendicular al plano tangente.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 5.1: Introducción a la UCM y Gravitación is shared under a not declared license and was authored, remixed, and/or curated by Boundless.