Saltar al contenido principal
LibreTexts Español

7.1: Introducción

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128315
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Momentum lineal

    El momento lineal es producto de la masa y velocidad de un objeto, se conserva en colisiones elásticas e inelásticas.

    objetivos de aprendizaje

    • Calcular el impulso de dos objetos en colisión

    En la mecánica clásica, el impulso lineal, o simplemente el momento (unidad SI kg m/s, o equivalentemente N s), es el producto de la masa y velocidad de un objeto. Matemáticamente se afirma como:

    \[\mathrm{p=mv}\]

    (Obsérvese aquí que p y v son vectores.) Al igual que la velocidad, el impulso lineal es una cantidad vectorial, que posee una dirección así como una magnitud. El impulso lineal es particularmente importante porque es una cantidad conservada, lo que significa que en un sistema cerrado (sin fuerzas externas) su impulso lineal total no puede cambiar.

    Debido a que el impulso tiene una dirección, se puede utilizar para predecir la dirección resultante de los objetos después de que chocan, así como sus velocidades. El momento se conserva tanto en colisiones inelásticas como elásticas. (La energía cinética no se conserva en colisiones inelásticas sino que se conserva en colisiones elásticas) Es importante señalar que si la colisión se produce en una superficie con fricción, o si hay resistencia al aire, necesitaríamos dar cuenta del impulso de los cuerpos que serían transferidos a la superficie y/ o aire.

    Echemos un vistazo a un ejemplo sencillo, unidimensional: El impulso de un sistema de dos partículas es la suma de sus momentos. Si dos partículas tienen masas m 1 y m 2, y velocidades v 1 y v 2, el momento total es:

    \[\mathrm{p=p_1+p_2=m_1v_1+m_2v_2.}\]

    Ten en cuenta que el momento y la velocidad son vectores. Por lo tanto, en 1D, si dos partículas se mueven en la misma dirección, v1 y v2 tienen el mismo signo. Si las partículas se mueven en direcciones opuestas tendrán signos opuestos.

    Si dos partículas se movieran en un avión elegiríamos nuestro plano XY para estar en el plano de movimiento. Entonces podemos escribir los componentes x e y del impulso total como:

    \[\begin{align} \mathrm{p_x} & \mathrm{=p_{1x}+p_{2x}=m_1v_{1x}+m_2v_{2x}} \\ \mathrm{p_y} & \mathrm{=p_{1y}+p_{2y}=m_1v_{1y}+m_2v_{2y}.} \end{align}\]

    Si el vector de impulso 2D se descompone en dos componentes, las ecuaciones para cada componente se reducen a sus equivalentes 1D.

    El impulso, al igual que la energía, es importante porque se conserva. “La cuna de Newton” que se muestra en es un ejemplo de conservación del impulso. Como discutiremos en el siguiente concepto (sobre Momentum, Force y Newton's Second Law), en la mecánica clásica, la conservación del impulso lineal está implícita en las leyes de Newton. Sólo unas pocas cantidades físicas se conservan en la naturaleza. El estudio de estas cantidades produce una visión fundamental de cómo funciona la naturaleza.

    imagen

    La Cuna de Newton: Se conserva el impulso total del sistema (o Cradle). (descuidando la pérdida por fricción en el sistema.)

    Momentum, Fuerza y Segunda Ley de Newton

    En la forma más general, la 2ª ley de Newton se puede escribir como\(\mathrm{F=\frac{dp}{dt}}\).

    objetivos de aprendizaje

    • Relacionar la Segunda Ley de Newton con el impulso y la fuerza

    En un sistema cerrado (uno que no intercambia materia alguna con el exterior y no es actuado por fuerzas externas), el impulso total es constante. Este hecho, conocido como la ley de conservación del impulso, está implícito en las leyes del movimiento de Newton. Supongamos, por ejemplo, que dos partículas interactúan. Debido a la tercera ley, las fuerzas entre ellas son iguales y opuestas. Si las partículas están numeradas 1 y 2, la segunda ley establece que

    \[\mathrm{\dfrac{dp_1}{dt}=−\dfrac{dp_2}{dt}}\]

    o

    \[\mathrm{\dfrac{d}{dt}(p_1+p_2)=0}\]

    Por lo tanto, el impulso total (p 1 + p 2) es constante. Si las velocidades de las partículas son u 1 y u2 antes de la interacción, y después son v 1 y v 2, entonces

    \[\mathrm{m_1u_1+m_2u_2=m_1v_1+m_2v_2}\]

    Esta ley se mantiene independientemente de la naturaleza de la fuerza interpartícula (o interna), por complicada que sea la fuerza entre las partículas. De igual manera, si hay varias partículas, el impulso intercambiado entre cada par de partículas se suma a cero, por lo que el cambio total en el momento es cero.

    Segunda Ley de Newton

    Newton en realidad declaró su segunda ley del movimiento en términos de impulso: La fuerza externa neta equivale al cambio de impulso de un sistema dividido por el tiempo durante el cual cambia. Usando símbolos, esta ley es

    \[\mathrm{F_{net}=\dfrac{Δp}{Δt},}\]

    donde\(\mathrm{F_{net}}\) está la fuerza externa neta,\(\mathrm{Δp}\) es el cambio de impulso, y\(\mathrm{Δt}\) es el cambio en el tiempo.

    Esta declaración de la segunda ley de movimiento de Newton incluye la más familiar\(\mathrm{F_{net}=ma}\( as a special case. We can derive this form as follows. First, note that the change in momentum \(\mathrm{Δp}\) que da\(\mathrm{Δp=Δ(mv)}\). Si la masa del sistema es constante, entonces\(\mathrm{Δ(mv)=mΔv}\). Entonces, para la masa constante, la segunda ley del movimiento de Newton se convierte en

    \[\mathrm{F_{net}=\dfrac{Δp}{Δt}=\dfrac{mΔv}{Δt}.}\]

    Porque\(\mathrm{\frac{Δv}{Δt}=a}\), obtenemos la ecuación familiar\(\mathrm{F_{net}=ma}\) cuando la masa del sistema es constante. La segunda ley del movimiento de Newton expresada en términos de impulso es más generalmente aplicable porque puede aplicarse a sistemas donde la masa está cambiando, como cohetes, así como a sistemas de masa constante.

    imagen

    Momentum en un Sistema Cerrado: En un juego de billar, el sistema de bolas enteras puede considerarse un sistema cerrado. Por lo tanto, se conserva el impulso total de las bolas.

    Impulso

    Impulso, o cambio de impulso, equivale a la fuerza externa neta promedio multiplicada por el tiempo en que actúa esta fuerza.

    objetivos de aprendizaje

    • Explicar la relación entre el cambio de impulso y la cantidad de tiempo que actúa una fuerza

    Impulso

    Las fuerzas producen aceleración o desaceleración en los cuerpos en movimiento, y cuanto mayor sea la fuerza que actúa sobre un objeto, mayor es su cambio de velocidad y, por lo tanto, mayor es su cambio en el momento. Sin embargo, el cambio de impulso también está relacionado con cuánto tiempo actúa la fuerza. Si se aplica una fuerza breve a un automóvil estancado, se produce un cambio en su impulso. La misma fuerza aplicada durante un período prolongado de tiempo produce un mayor cambio en el impulso del automóvil. La cantidad de impulso es fuerza × intervalo de tiempo, o en notación abreviada:

    Momentum & Impulse: Una breve descripción del impulso y el impulso para estudiantes de física de secundaria.

    \[\mathrm{Impulse=FΔt,}\]

    donde F es la fuerza neta en el sistema, y Δt es la duración de la fuerza.

    De la 2da ley de Newton:

    \[\mathrm{F = \dfrac{\Delta p}{\Delta t} \; (\Delta p: change \; in \; momentum),}\]

    cambio de impulso es igual a la fuerza externa neta promedio multiplicada por el tiempo que esta fuerza actúa.

    \[\mathrm{Δp=FΔt.}\]

    Por lo tanto, el impulso como se define en el párrafo anterior es simplemente equivalente a p.

    Una fuerza sostenida durante mucho tiempo produce más cambios en el momento que la misma fuerza aplicada brevemente. Una pequeña fuerza aplicada durante mucho tiempo puede producir el mismo cambio de momento que una gran fuerza aplicada brevemente porque es el producto de la fuerza y el tiempo para el que se aplica lo que es importante. El impulso siempre es igual al cambio de momento y se mide en Ns (Newton segundos), ya que tanto la fuerza como el intervalo de tiempo son importantes para cambiar el momento.

    Nuestra definición de impulso incluye una suposición de que la fuerza es constante a lo largo del intervalo de tiempo\(\mathrm{Δt}\). Las fuerzas no suelen ser constantes. Las fuerzas varían considerablemente incluso durante los breves intervalos de tiempo considerados. Sin embargo, es posible encontrar una fuerza efectiva promedio\(\mathrm{F_{eff}}\) que produzca el mismo resultado que la correspondiente fuerza variable en el tiempo. Muestra una gráfica de cómo se ve una fuerza real en función del tiempo para una pelota que rebota en el piso. El área bajo la curva tiene unidades de impulso y es igual al impulso o cambio de impulso entre tiempos\(\mathrm{t_1}\) y\(\mathrm{t_2}\). Esa área es igual al área dentro del rectángulo delimitada por\(\mathrm{F_{eff}, t_1,}\) y\(\mathrm{t_2}\). Así, los impulsos y sus efectos son los mismos tanto para las fuerzas reales como para las efectivas. Equivalentemente, podemos encontrar el área bajo la curva F (t) entre\(\mathrm{t_1}\) y\(\mathrm{t_2}\) para calcular el impulso en forma matemática:

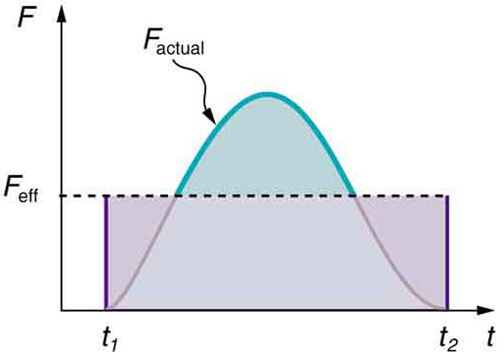
    imagen

    Fuerza vs Tiempo: Un gráfico de fuerza versus tiempo con tiempo a lo largo del eje x y fuerza a lo largo del eje y para una fuerza real y una fuerza efectiva equivalente. Las áreas bajo las dos curvas son iguales.

    \[\mathrm{Impulse=\int_{t_1}^{t_2} F(t)dt.}\]

    Puntos Clave

    • Al igual que la velocidad, el impulso lineal es una cantidad vectorial, que posee una dirección así como una magnitud.
    • El impulso, como la energía, es importante porque es una cantidad conservada.
    • El impulso de un sistema de partículas es la suma de sus momentos. Si dos partículas tienen masas m 1 y m 2, y velocidades v 1 y v 2, el momento total es\(\mathrm{p=p_1+p_2=m_1v_1+m_2v_2.}\).
    • En un sistema cerrado, sin fuerzas externas, el impulso total es constante.
    • La ecuación familiar\(\mathrm{F=ma}\) es un caso especial de la forma más general de la segunda ley cuando la masa del sistema es constante.
    • La conservación del momento se mantiene (en ausencia de fuerza externa) independientemente de la naturaleza de la fuerza interpartícula (o interna), por complicada que sea la fuerza entre las partículas.
    • Una pequeña fuerza aplicada durante mucho tiempo puede producir el mismo cambio de momento que una gran fuerza aplicada brevemente, porque es el producto de la fuerza y el tiempo para el que se aplica lo que es importante.
    • Una fuerza produce una aceleración, y cuanto mayor es la fuerza que actúa sobre un objeto, mayor es su cambio de velocidad y, por lo tanto, mayor es su cambio de impulso. Sin embargo, el cambio de impulso también está relacionado con cuánto tiempo actúa la fuerza.
    • En caso de una fuerza variable en el tiempo, el impulso se puede calcular integrando la fuerza a lo largo de la duración del tiempo. \(\mathrm{Impulse=\int_{t_1}^{t_2} F(t)dt.}\).

    Términos Clave

    • inelástica: (Como referida a una colisión inelástica, a diferencia de una colisión elástica.) Una colisión en la que no se conserva la energía cinética.
    • colisión elástica: Un encuentro entre dos cuerpos en el que la energía cinética total de los dos cuerpos después del encuentro es igual a su energía cinética total antes del encuentro. Las colisiones elásticas ocurren solo si no hay conversión neta de energía cinética en otras formas.
    • conservación: Una propiedad medible particular de un sistema físico aislado no cambia a medida que evoluciona el sistema.
    • sistema cerrado: Un sistema físico que no intercambia ninguna materia con su entorno y no está sujeto a ninguna fuerza cuya fuente sea externa al sistema.
    • momentum: (de un cuerpo en movimiento) producto de su masa y velocidad.
    • impulso: La integral de la fuerza a lo largo del tiempo.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 7.1: Introducción is shared under a not declared license and was authored, remixed, and/or curated by Boundless.