Saltar al contenido principal
LibreTexts Español

7.5: Centro de Masa

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128329
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Identificar el centro de masa de un objeto con distribución continua de masa

    En los módulos anteriores sobre “Centro de Masa y Movimiento Traslacional”, aprendimos por qué el concepto de centro de masa (COM) ayuda a resolver problemas mecánicos que involucran un cuerpo rígido. Aquí, estudiaremos la definición rigurosa de COM y cómo determinar la ubicación de la misma. La posición del COM es el promedio ponderado en masa de las posiciones de las partículas.

    Definición: centro de masa

    El centro de masa es una declaración de disposición espacial de la masa (es decir, distribución de la masa dentro del sistema). A la posición de COM se le da una formulación matemática que implica la distribución de la masa en el espacio:

    \[\mathrm{r_{COM}=\dfrac{∑_i m_ir_i}{M},}\]

    donde r COM y r i son vectores que representan la posición de COM e i-ésima partícula respectivamente, y M y mi son la masa total y masa de la i-ésima partícula, respectivamente. Esta media significa que la posición del COM es el promedio ponderado en masa de las posiciones de las partículas.

    Objeto con Distribución Masiva Continua

    Si la distribución de masa es continua con la densidad ρ (r) dentro de un volumen V, la posición de COM se da como

    \[\mathrm{r_{COM}=\dfrac{1}{M} \int _V ρ(r)rdV,}\]

    donde M es la masa total en el volumen. Si una distribución continua de masa tiene densidad uniforme, lo que significa que ρ es constante, entonces el centro de masa es el mismo que el centro del volumen.

    Localización del Centro de Masa

    La determinación experimental del centro de masa de un cuerpo utiliza fuerzas de gravedad sobre el cuerpo y se basa en el hecho de que en el campo de gravedad paralelo cerca de la superficie de la Tierra el centro de masa es el mismo que el centro de gravedad.

    El centro de masa de un cuerpo con un eje de simetría y densidad constante debe estar sobre este eje. Así, el centro de masa de un cilindro circular de densidad constante tiene su centro de masa en el eje del cilindro. De la misma manera, el centro de masa de un cuerpo esféricamente simétrico de densidad constante se encuentra en el centro de la esfera. En general, para cualquier simetría de un cuerpo, su centro de masa será un punto fijo de esa simetría.

    En dos dimensiones: Un método experimental para localizar el centro de masa es suspender el objeto desde dos ubicaciones y dejar caer plomadas desde los puntos de suspensión. La intersección de las dos líneas es el centro de masa.

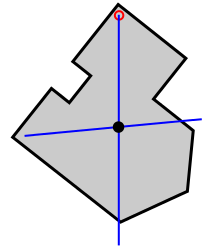
    imagen

    Método de plomada para el centro de masa: Suspender el objeto desde dos ubicaciones y dejar caer las plomadas desde los puntos de suspensión. La intersección de las dos líneas es el centro de masa.

    En tres dimensiones: Al soportar un objeto en tres puntos y medir las fuerzas que resisten el peso del objeto, se puede determinar COM de las coordenadas tridimensionales del centro de masa.

    Movimiento del Centro de Masa

    Podemos describir el movimiento traslacional de un cuerpo rígido como si se tratara de una partícula puntual con la masa total ubicada en el centro de masa COM.

    objetivos de aprendizaje

    • Derivar el centro de masa para el movimiento de traslación de un cuerpo rígido

    Podemos describir el movimiento traslacional de un cuerpo rígido como si se tratara de una partícula puntual con la masa total localizada en el centro de masa (COM). En este Atom. probaremos que la masa total (M) multiplicada por la aceleración de la COM (a COM), efectivamente, es igual a la suma de las fuerzas externas. Es decir,

    \[\mathrm{M \cdot a_{COM}=∑F_{ext}.}\]

    Se puede ver que la 2da ley de Newton se aplica como si estuviéramos describiendo el movimiento de una partícula puntual (con masa M) bajo la influencia de la fuerza externa.

    Derivación

    A partir de la definición del centro de masa,

    \[\mathrm{r_{COM}=\dfrac{∑_i m_ir_i}{M},}\]

    obtenemos\(\mathrm{M⋅a_{COM}=∑m_ia_i}\) tomando tiempo derivado dos veces en cada lado.

    Tenga en cuenta que\(\mathrm{∑m_ia_i=∑F_i}\).

    En un sistema de partículas, cada partícula puede sentir fuerzas tanto externas como internas. Aquí, las fuerzas externas son fuerzas de fuentes externas, mientras que las fuerzas internas son fuerzas entre partículas en el sistema. Dado que la suma de todas las fuerzas internas será 0 debido a la tercera ley de Newton,

    \(\mathrm{∑F_i=∑F_{i,ext}}\). Por lo tanto, obtenemos\(\mathrm{M \cdot a_{COM}=∑F_{ext}.}\)

    Por ejemplo, cuando confinamos nuestro sistema a la Tierra y a la Luna, la fuerza gravitacional debida al Sol sería externa, mientras que la fuerza gravitacional sobre la Tierra debida a la Luna (y viceversa) sería interna. Dado que las fuerzas gravitacionales entre la Tierra y la Luna son iguales en magnitud y opuestas en dirección, se cancelarán entre sí en la suma (ver).

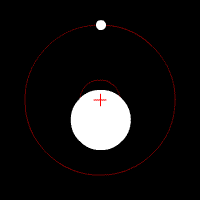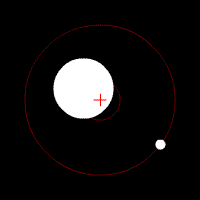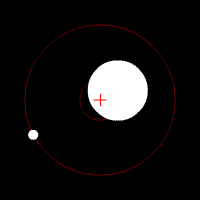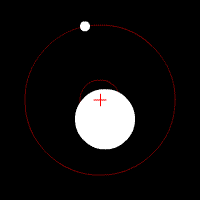
    imagen

    COM de la Tierra y la Luna: Tierra y Luna orbitando un COM dentro de la Tierra. La cruz roja representa el COM del sistema de dos cuerpos. El COM orbitará alrededor del Sol como si se tratara de una partícula puntual.

    Corolario

    Cuando no hay fuerza externa, se conserva el impulso COM.

    Prueba: Dado que no hay fuerza externa,\(\mathrm{M \cdot a_{COM}=0}\). Por lo tanto,

    \(\mathrm{M \cdot v_{COM}=constant.}\)

    Prueba

    Como no hay fuerza externa,

    \[M⋅a_{COM}=0.\]

    Por lo tanto,

    \(M⋅v_{COM}=constant\).

    \(\square\)

    Centro de Masa del Cuerpo Humano

    El centro de masa (COM) es un concepto físico importante, es el punto sobre el que giran los objetos.

    objetivos de aprendizaje

    • Estimar el COM de un objeto dado

    El centro de masa (COM) es un concepto físico importante. Es el punto de un objeto en el que la posición relativa ponderada de la masa distribuida se suma a cero, el punto sobre el cual giran los objetos.

    Las proporciones humanas han sido importantes en el arte, la medición y la medicina (un dibujo bien conocido del cuerpo humano se ve en). Aunque el cuerpo humano tiene características complicadas, la ubicación del centro de masa (COM) podría ser un buen indicador de las proporciones corporales. El centro de masa del cuerpo humano depende del género y la posición de las extremidades. En una postura de pie, suele ser unos 10 cm más bajo que el ombligo, cerca de la parte superior de los huesos de la cadera. En este Átomo, aprenderemos a medir el COM de un cuerpo humano.

    imagen

    “El hombre vitruviano” de Leonardo da Vinci: El hombre vitruviano: Un dibujo creado por Leonardo da Vinci. El dibujo se basa en las correlaciones de proporciones humanas ideales con la geometría descrita [4] por el antiguo arquitecto romano Vitruvio en el Libro III de su tratado De Architectura.

    Ejemplo\(\PageIndex{1}\):

    Primero, tomemos dos escamas y una viga de madera (H metro de largo), lo suficientemente larga como para contener todo el cuerpo del sujeto. Coloque las escalas H metros aparte, y coloque la viga a través de las escalas, como se ilustra en. Ahora, que el sujeto se acueste sobre la viga. Asegúrese de que sus talones estén alineados con un extremo de la viga. Mida las lecturas (F 1, F 2) en la escala.

    imagen

    El COM de un cuerpo humano: Esta figura demuestra medir el COM de un cuerpo humano.

    El sistema (persona+haz) tiene tres fuerzas externas: gravedad sobre el sujeto (F CM), y fuerzas normales de las escalas F 1 y F 2. La ecuación de movimiento por fuerza (f=mA) nos dará:

    \[\mathrm{F1+F2=Mg,}\]

    donde M es masa del sujeto. (Suponemos que la viga de madera no tiene masa.) Esta ecuación no proporciona toda la información para localizar el COM. Sin embargo, la ecuación de movimiento para par\(\mathrm{(τ=Iα)}\) ayuda.

    Dado que el par neto del sistema es cero (por lo tanto, no hay aceleración rotacional),

    \[\mathrm{hF_2−(H−h)F_1=0. (h: COM \; height)}\]

    El COM se elige como origen para el par. Por lo tanto, la gravedad no aporta nada como par. Resolviendo para h y usando la ecuación de movimiento para fuerza, obtenemos

    \[\mathrm{h=\dfrac{HF_1}{Mg}.}\]

    Centro de Masa y Movimiento Traslacional

    El COM (centro de masa) de un sistema de partículas es un punto geométrico que asume toda la masa y fuerza (s) externa (s) durante el movimiento.

    objetivos de aprendizaje

    • Apoyar la presencia de COM en cuerpos tridimensionales en movimiento

    Introducción: COM, Momentum Lineal y Colisiones

    Nuestro estudio del movimiento se ha limitado hasta este punto. Nos hemos referido a partículas, objetos y cuerpos de la misma manera. Consideramos que los cuerpos rígidos tridimensionales reales se mueven de tal manera que todas las partículas constituyentes tuvieron el mismo movimiento (es decir, misma trayectoria, velocidad y aceleración). Al hacer esto, hemos considerado esencialmente un cuerpo rígido como una partícula puntual.

    Centro de Masa (COM)

    Un cuerpo real, sin embargo, puede moverse de manera diferente a este paradigma simplificado. Considera una pelota rodando por un plano de inclinación o un palo arrojado al aire. Diferentes partes de un cuerpo tienen diferentes movimientos. Mientras se traslada en el aire, el palo gira alrededor de un eje móvil, como se muestra en. Esto significa que tales cuerpos pueden no comportarse como una partícula puntual, como se sugirió anteriormente.

    imagen

    Fuerzas en la COM: Izquierda: La fuerza parece operar en la COM es “mgsinθ. Derecha: La fuerza parece operar en el COM es “mg”.

    Describir movimientos de partes o partículas que tienen diferentes movimientos sería bastante complicado de hacer de manera integrada. Sin embargo, tales cuerpos tridimensionales en movimiento tienen una característica sorprendente y simplificadora: un punto geométrico que se comporta como una partícula. A este punto se le conoce como centro de masa, abreviado COM (la definición matemática de COM se introducirá en el próximo Átomo sobre “Localización del Centro de Masa”). Tiene los dos aspectos caracterizantes siguientes:

    • El centro de masa parece llevar toda la masa del cuerpo.
    • En el centro de masa, todas las fuerzas externas parecen aplicarse.

    Significativamente, el centro de una bola (el COM de una bola rodante) sigue una trayectoria lineal recta; mientras que el COM de una varilla sigue una trayectoria parabólica (como se muestra en la figura anterior). En segundo lugar, las fuerzas parecen operar sobre las COMs en dos casos (“mgsinθ y “mg”) como si de hecho fueran objetos parecidos a partículas. Este concepto de COM, por lo tanto, elimina las complejidades por lo demás presentes al intentar describir movimientos de cuerpos rígidos.

    Descripción del movimiento en un cuerpo rígido

    Podemos describir el movimiento general de un objeto (con masa m) de la siguiente manera:

    • Describimos el movimiento traslacional de un cuerpo rígido como si se tratara de una partícula puntual con masa m ubicada en COM.
    • La rotación de la partícula, con respecto al COM, se describe de manera independiente.

    “Separamos” la parte traslacional del movimiento de la parte rotacional. Al introducir el concepto de COM, el movimiento traslacional se convierte en el de una partícula puntual con masa m, lo que simplifica significativamente la complejidad matemática del problema.

    Puntos Clave

    • El centro de masa (COM) es una declaración de disposición espacial de la masa (es decir, distribución de la masa dentro del sistema).
    • La determinación experimental del centro de masa de un cuerpo utiliza fuerzas de gravedad sobre el cuerpo y se basa en el hecho de que en el campo de gravedad paralelo cerca de la superficie de la tierra el centro de masa es el mismo que el centro de gravedad.
    • Para un objeto 2D, un método experimental para localizar el centro de masa es suspender el objeto desde dos ubicaciones y soltar plomadas desde los puntos de suspensión. La intersección de las dos líneas es el centro de masa.
    • La masa total multiplicada por la aceleración del centro de masa equivale a la suma de las fuerzas externas.
    • Para el movimiento traslacional de un cuerpo rígido con masa M, la segunda ley de Newton se aplica como si estuviéramos describiendo el movimiento de una partícula puntual (con masa M) bajo la influencia de la fuerza externa.
    • Cuando no hay fuerza externa, se conserva el impulso del centro de masa.
    • Si bien un cuerpo humano presenta características complicadas, la ubicación del centro de masa (COM) podría ser un buen indicador de las proporciones corporales.
    • Podemos medir la ubicación de COM con dos escalas y una viga de madera. Las ecuaciones lineales y rotacionales del movimiento nos dan la ubicación.
    • El centro de masa del cuerpo humano depende del género y la posición de las extremidades. En una postura de pie, suele ser unos 10 cm más bajo que el ombligo, cerca de la parte superior de los huesos de la cadera.
    • En un movimiento de un cuerpo rígido, diferentes partes del cuerpo tienen movimientos diferentes.Esto significa que estos cuerpos pueden no comportarse como una partícula puntual.
    • Hay un punto geométrico característico del cuerpo tridimensional en movimiento. Este punto se comporta como una partícula, y se le conoce como centro de masa, abreviado COM. COM parece llevar toda la masa del cuerpo. Todas las fuerzas externas parecen aplicarse en COM.
    • Para describir el movimiento de un cuerpo rígido (posiblemente con una geometría complicada), separamos la parte traslacional del movimiento de la parte rotacional.

    Términos Clave

    • plomada: Un cordón con un peso unido, utilizado para producir una línea vertical.
    • cuerpo rígido: Un sólido idealizado cuyo tamaño y forma son fijos y permanecen inalterados cuando se aplican fuerzas; utilizado en la mecánica newtoniana para modelar objetos reales.
    • centro de masa: El centro de masa (COM) es el punto único en el centro de una distribución de masa en el espacio que tiene la propiedad de que los vectores de posición ponderados relativos a este punto suman a cero.
    • par: Un efecto de rotación o torsión de una fuerza; (unidad SI newton-metro o Nm; unidad imperial pie-libra o ft-lb)
    • partícula puntual: Una idealización de partículas muy utilizadas en física. Su característica definitoria es que carece de extensión espacial, lo que significa que geométricamente la partícula es equivalente a un punto.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 7.5: Centro de Masa is shared under a not declared license and was authored, remixed, and/or curated by Boundless.