23A: Estática

Debe repetirse: Asegurarse de que cualquier fuerza que entre en la ecuación de equilibrio de par se multiplique por un brazo de momento, y que cualquier par puro (como τo en la solución del ejemplo 23-2 en la página 151) que ingrese a la ecuación de equilibrio de par NO se multiplica por un brazo de momento.

Para cualquier cuerpo rígido, en cualquier instante en el tiempo, la ^2ª Ley de Newton para el movimiento traslacional

\[\vec{a}=\frac{1}{m} \sum \vec{F}\]

y la ^2ª Ley de Newton para el Movimiento Rotacional

\[\vec{\propto}=\frac{1}{I} \sum \vec{\tau}\]

ambos aplican. En este capítulo nos enfocamos en cuerpos rígidos que están en equilibrio. A este tema, el estudio de los objetos en equilibrio, se le conoce como estática. Estar en equilibrio significa que la aceleración y la aceleración angular del cuerpo rígido en cuestión son ambas cero. Cuando\(\vec{a}=0\), la 2da Ley de Newton para el movimiento traslacional se reduce a

\[\sum \vec{F}=0 \label{23-1}\]

y cuando\(\vec{\propto}=0\), la 2da Ley de Newton para el movimiento rotacional se convierte en

\[\sum \vec{\tau}=0 \label{23-2}\]

Estas dos ecuaciones vectoriales se denominan ecuaciones de equilibrio. También se les conoce como las condiciones de equilibrio. En que cada uno de los vectores tiene tres componentes, las dos ecuaciones vectoriales en realidad representan un conjunto de seis ecuaciones escalares:

\[\sum F_x=0 \]

\[\sum F_y=0 \]

\[\sum F_z=0 \]

\[\sum \tau_{x \circlearrowleft}=0 \]

\[\sum \tau_{y \circlearrowleft}=0 \]

\[\sum \tau_{z \circlearrowleft}=0 \]

En muchos casos, todas las fuerzas se encuentran en un mismo plano, y si hay pares aparte de los pares resultantes de las fuerzas, esos pares están alrededor de un eje perpendicular a ese plano. Si definimos el plano en el que se encuentran las fuerzas para que sea el\(x-y\) plano, entonces para tales casos, el conjunto de seis ecuaciones escalares se reduce a un conjunto de 3 ecuaciones escalares (en que las otras 3 son\(0=0\) identidades triviales):

\[\sum F_x=0 \label{23-3}\]

\[\sum F_y=0 \label{23-4}\]

\[\sum \tau_{z \circlearrowleft}=0 \label{23-5}\]

Los problemas estáticos representan un subconjunto de los problemas de la ^2ª Ley de Newton. Ya sabes cómo resolver los problemas de la ^2ª Ley de Newton así que no hay muchas novedades para que aprendas aquí, pero un par de detalles sobre la forma en que se soportan los objetos te serán útiles.

Muchos problemas estáticos involucran vigas y columnas. Las vigas y columnas se denominan colectivamente miembros. El análisis del equilibrio de un miembro generalmente implica algunas aproximaciones que implican el descuido de algunas distancias cortas. Siempre y cuando estas distancias sean pequeñas en comparación con la longitud de la viga, las aproximaciones son muy buenas. Una de estas aproximaciones es que, a menos que se especifique lo contrario, descuidamos las dimensiones de la sección transversal del miembro (por ejemplo, la anchura y altura de una viga). No descuidamos la duración del miembro.

Miembros Conectados por Pines

Un pasador es un eje corto. Un miembro que está conectado por un pasador en un extremo, es libre de girar alrededor del pasador. El pasador es perpendicular a la dirección en la que se extiende el miembro. En la práctica, en el caso de un miembro que está conectado por pasador en un extremo, el pasador no está realmente justo al final del miembro, pero a menos que se especifique la distancia desde el pasador hasta el extremo (el extremo que está muy cerca del pasador) del miembro, descuidamos esa distancia. Además, el mecanismo por el cual una viga se conecta por pasador a, por ejemplo, una pared, hace que el extremo de la viga esté a una corta distancia de la pared. A menos que se especifique lo contrario, se supone que debemos descuidar esta distancia también. Un pasador ejerce una fuerza sobre el miembro. La fuerza se encuentra en el plano que contiene el miembro y es perpendicular al pasador. Más allá de eso, se desconoce la dirección de la fuerza, inicialmente,. En un diagrama de cuerpo libre del miembro, se puede incluir la fuerza del pasador como una fuerza desconocida en un ángulo desconocido, o se pueden incluir los componentes x e y desconocidos de la fuerza del pasador.

Un extremo de una viga de masa 6.92 kg y de longitud 2.00 m está conectado por pasador a una pared. El otro extremo de la viga descansa sobre un piso sin fricción en un punto que está a 1.80 m de distancia de la pared. La viga se encuentra en un plano que es perpendicular tanto a la pared como al piso. El pasador es perpendicular a ese plano. Encuentra la fuerza ejercida por el pasador en la viga, y encuentra la fuerza normal ejercida sobre la viga por el piso.

Solución

Primero dibujemos un boceto:

Ahora dibujamos un diagrama de cuerpo libre del miembro:

Vamos a necesitar aplicar la condición de equilibrio de par a la viga así que voy a agregar brazos de momento al diagrama. Mi plan es sumar los pares sobre el punto O así representaré brazos de momento con respecto a un eje a través del punto O.

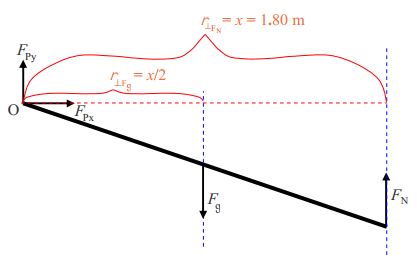
Ahora vamos a aplicar las condiciones de equilibrio:

\[\sum F_{\rightarrow}=0 \]

\[F_{Px}=0\]

Hay tres valores de fuerza desconocidos representados en el diagrama de cuerpo libre y ¡ya encontramos uno de ellos! Apliquemos otra condición de equilibrio:

\[F_{\uparrow}=0\]

\[F_{Py}-F_g+F_N=0\]

\[F_{Py}-mg+F_N=0 \label{23-6}\]

Hay dos incógnitas en esta ecuación. No podemos resolverlo pero puede resultar útil más adelante. Apliquemos la condición de equilibrio de par.

\[\sum \tau_{\circ \circlearrowleft}=0\]

\[-\dfrac{x}{2} F_g+xF_N=0\]

\[-\dfrac{x}{2}mg+xF_N=0\]

Aquí, copia esa última línea para usted antes de continuar:

\[-\dfrac{x}{2}mg+xF_N=0\]

\[F_N=\dfrac{mg}{2}\]

\[F_N=\dfrac{6.92kg(9.80 N/kg)}{2}\]

\[F_N=32.9N\]

Podemos usar este resultado\((F_N=\frac{mg}{2})\) en Ecuación\(\ref{23-6}\) para obtener un valor para\(F_Py\):

\[F_{Py}-mg+F_N=0\]

\[F_{Py}=mg-F_N\]

\[F_{Py}=mg-\dfrac{mg}{2}\]

\[F_{Py}=\dfrac{mg}{2}\]

\[F_{Py}=\frac{6.92kg(9.80N/kg)}{2}\]

\[F_{Py}=32.9N\]

Recordando que encontramos\(F_{Px}\) cero, podemos escribir, para nuestra respuesta final:

\[\vec{F_p}=32.9 \quad \mbox{newtons, straight upward and}\]

\[\vec{F_N}\quad \mbox{newtons, straight upward}\]

Miembros Fix-Connected

Un miembro fijo conectado es aquel que está rígidamente unido a una estructura (como una pared) que es externa al objeto cuyo equilibrio está en estudio. Un ejemplo sería una varilla metálica, uno de cuyos extremos está soldado a una pared metálica. Una conexión fija puede aplicar una fuerza en cualquier dirección y puede aplicar un par en cualquier dirección. Cuando todas las demás fuerzas se encuentran en un plano, la fuerza aplicada por la conexión fija estará en ese plano. Cuando todos los demás pares están a lo largo o paralelos a una línea en particular, entonces el par ejercido por la conexión fija será a lo largo o paralelo a esa misma línea.

Una barra horizontal de longitud L y masa\(m\) is fix connected to a wall. Find the force and the torque exerted on the bar by the wall.

Solution

First a sketch:

then a free body diagram:

followed by the application of the equilibrium conditions to the free body diagram:

\[\sum F_{\rightarrow}=0 \]

\[F_{ox}=0\]

That was quick. Let’s see what setting the sum of the vertical forces equal to zero yields:

\[\sum F_{\uparrow}=0\]

\[F_{oy}-F_g=0\]

\[F_{oy}=F_g\]

\[F_{oy}=mg \]

Now for the torque equilibrium condition:

\[\sum \tau_{\circ \circlearrowleft}=0\]

\[\tau_{\circ}-\frac{L}{2}F_g=0\]

\[\tau_{\circ}-\frac{L}{2} mg=0\]

\[\tau_{\circ}=\frac{1}{2}mgL\]

The wall exerts an upward force of magnitude \(mg\), and a counterclockwise (as viewed from that position for which the free end of the bar is to the right) torque of magnitude \(\frac{1}{2}mgL\) on the bar.