2.2: Aceleración

Aceleración media e instantánea

Así como definimos la velocidad promedio en el capítulo anterior, usando el concepto de desplazamiento (o cambio de posición) a lo largo de un intervalo de tiempo\(\Delta t\), definimos la aceleración promedio a lo largo del tiempo\(\Delta t\) usando el cambio de velocidad:

\[ a_{a v}=\frac{\Delta v}{\Delta t}=\frac{v_{f}-v_{i}}{t_{f}-t_{i}} \label{eq:2.1} .\]

Aquí,\(v_i\) y\(v_f\) están las velocidades inicial y final, respectivamente, es decir, las velocidades al principio y al final del intervalo de tiempo\(\Delta t\). Sin embargo, como fue el caso de la velocidad promedio, la aceleración promedio es un concepto de utilidad algo limitada, por lo que también podríamos proceder de inmediato a la definición de la aceleración instantánea (o simplemente “la” aceleración, sin modificadores), a través del mismo tipo de limitación proceso por el cual definimos la velocidad instantánea:

\[ a=\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t} \label{eq:2.2} .\]

Todo lo que dijimos en el capítulo anterior sobre la relación entre velocidad y posición ahora se puede decir sobre la relación entre aceleración y velocidad. Por ejemplo (si conoces el cálculo), la aceleración en función del tiempo es la derivada de la velocidad en función del tiempo, lo que la convierte en la segunda derivada de la función position:

\[ a=\frac{d v}{d t}=\frac{d^{2} x}{d t^{2}} \label{eq:2.3} \]

(y si aún no conoces el cálculo, ¡no te preocupes por los superíndices “2” en esa última expresión! Es solo una notación extraña que algún día aprenderás.)

De igual manera, podemos “leer” la aceleración instantánea de una gráfica de velocidad versus tiempo, observando la pendiente de la línea tangente a la curva en cualquier punto. No obstante, si lo que se nos da es un gráfico de posición versus tiempo, la conexión a la aceleración es más indirecta. La figura te\(\PageIndex{1}\) proporciona un ejemplo de este tipo. A ver si puedes adivinar en qué puntos a lo largo de esta curva la aceleración es positiva, negativa o cero.

La manera de hacer esto “desde cero”, por así decirlo, es tratar de averiguar qué está haciendo la velocidad, primero, e inferir la aceleración a partir de eso. Así es como iría eso:

Comenzando en\(t\) = 0, y vigilando la pendiente de la\(t\) curva\(x\) -vs-, podemos ver que la velocidad comienza en cero o cerca de cero y aumenta de manera constante por un tiempo, hasta que\(t\) es un poco más de 2 s (digamos,\(t\) = 2.2 s por definición). Eso correspondería a un periodo de aceleración positiva, ya que\(\Delta v\) sería positivo para cada uno\(\Delta t\) en ese rango.

Figura\(\PageIndex{1}\): Una posible gráfica de posición vs. tiempo para un objeto cuya aceleración cambia con el tiempo.

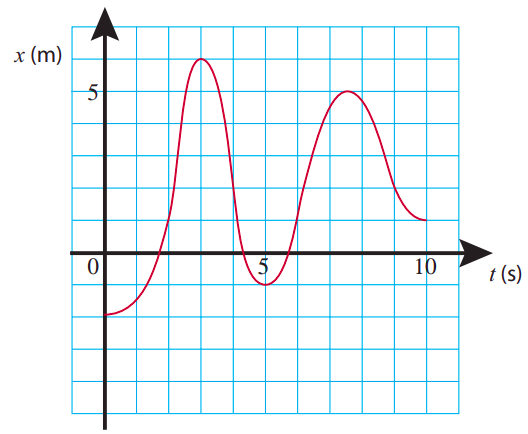
Entre\(t\) = 2.2 s y\(t\) = 2.5 s, a medida que el objeto se mueve de\(x\)\(x\) = 2 m a = 4 m, la velocidad no parece cambiar mucho, y la aceleración correspondientemente sería cero o cercana a cero. Entonces, alrededor de\(t\) = 2.5 s, la velocidad comienza a disminuir notablemente, volviéndose (instantáneamente) cero a\(t\) =3 s (\(x\)= 6 m). Eso correspondería a una aceleración negativa. Tenga en cuenta, sin embargo, que la velocidad después sigue disminuyendo, volviéndose cada vez más negativa hasta alrededor de\(t\) = 4 s. Esto también corresponde a una aceleración negativa: aunque el objeto se está acelerando, se está acelerando en la dirección negativa, así\(\Delta v\), y por lo tanto\(a\), es negativo para cada intervalo de tiempo allí. Concluimos que\(a < 0\) para todos los tiempos entre\(t\) = 2.5 s y\(t\) = 4 s.

A continuación, como simplemente miramos pasado\(t\) = 4 s, sucede algo más interesante: el objeto sigue yendo en la dirección negativa (velocidad negativa), pero ahora se está desacelerando. Matemáticamente, eso corresponde a una aceleración positiva, ya que el valor algebraico de la velocidad de hecho está aumentando (un número como −3 es mayor que un número como −5). Otra forma de pensarlo es que, si tenemos cada vez menos cosa negativa, nuestra tendencia general es positiva. Entonces la aceleración es positiva desde\(t\) = 4 s hasta\(t\) = 5 s (donde la velocidad es instantáneamente cero a medida que la dirección del movimiento del objeto se invierte), y más allá, hasta aproximadamente\(t\) = 6 s, ya que entre\(t\) = 5 s y\(t\) = 6 s la velocidad es positiva y Creciendo.

Probablemente puedas averiguar por tu cuenta ahora qué sucede después de\(t\) = 6 s, razonando como lo hice anteriormente, pero también puedes haber notado un patrón que facilita mucho este tipo de análisis. La aceleración (como pueden haber entendido ya aquellos con conocimiento de cálculo), al ser proporcional a la segunda derivada de la función\(x(t)\) respecto a\(t\), está directamente relacionada con la curvatura de la\(x\) -vs-\(t\) gráfica. Como muestra la\(\PageIndex{2}\) siguiente figura, si la gráfica es cóncava (a veces llamada “cóncava hacia arriba”), la aceleración es positiva, mientras que es negativa siempre que la gráfica sea convexa (o “cóncava hacia abajo”). Es (instantáneamente) cero en aquellos puntos donde cambia la curvatura (que quizás conozcas como puntos de inflexión), así como en tramos de tiempo cuando el\(t\) gráfico\(x\) -vs- es una línea recta (movimiento con velocidad constante).

Figura\(\PageIndex{2}\): Cómo se ven\(t\) las curvas\(x\) -vs- para los diferentes signos posibles de la aceleración.

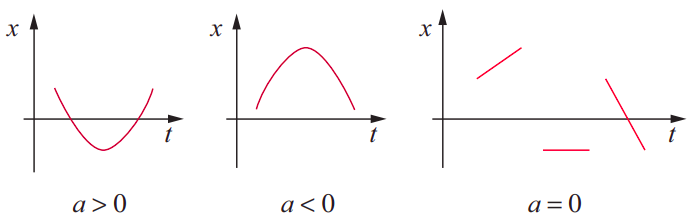
La figura\(\PageIndex{3}\) muestra la posición, velocidad y aceleración versus tiempo para un caso de movimiento hipotético. Por favor, estudiarlo cuidadosamente hasta que cada característica de cada gráfica tenga sentido, en relación con los otros dos! Verás muchos otros ejemplos de esto en la tarea y el laboratorio.

Figura\(\PageIndex{3}\): Gráficas de posición, velocidad y aceleración vs. tiempo de la muestra para movimiento con aceleración constante por tramos.

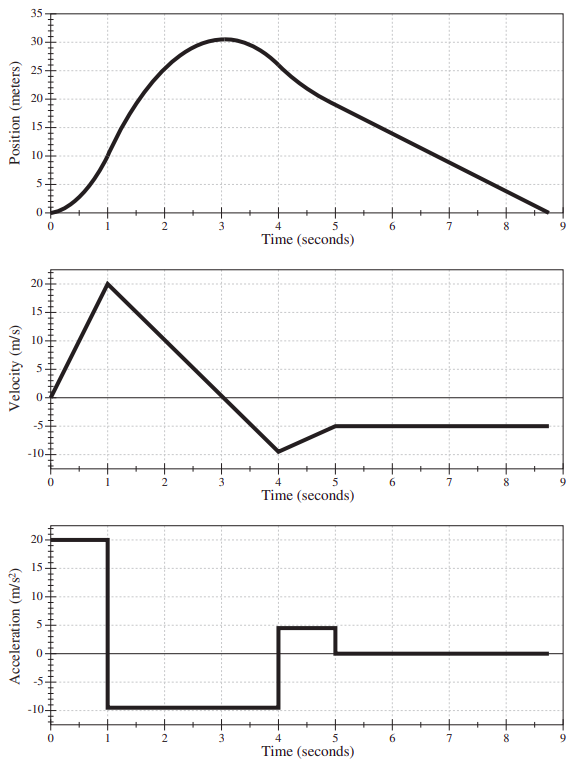
Observe que, en todas estas cifras, el signo de\(x\) o\(v\) en un momento dado no tiene nada que ver con el signo de\(a\) en ese mismo tiempo. Es cierto que, por ejemplo, un negativo\(a\), si se mantiene durante un tiempo suficientemente largo, eventualmente resultará en un negativo\(v\) (como sucede, por ejemplo, en la Figura\(\PageIndex{3}\) sobre el intervalo de\(t\) = 1 a\(t\) = 4 s) pero esto puede llevar mucho tiempo, dependiendo del tamaño de \(a\)y el valor inicial de\(v\). Las pistas gráficas a seguir, en cambio, son: la aceleración viene dada por la pendiente de la tangente a la\(t\) curva\(v\) -vs-, o la curvatura de la\(t\) curva\(x\) -vs-, como se explica en la Figura\(\PageIndex{2}\); y la velocidad viene dada por la pendiente de la tangente a la\(x\) - vs-\(t\) curva.

(Nota: Para\(\PageIndex{3}\) simplificar la interpretación de Figura, he elegido la aceleración para que sea “constante por partes”, es decir, constante a lo largo de intervalos de tiempo prolongados y cambiando de valor de manera discontinua de un intervalo al siguiente. Esto es físicamente poco realista: en cualquier situación de la vida real, se esperaría que la aceleración cambiara más o menos suavemente de instante a instante. Veremos ejemplos de eso más adelante, cuando empecemos a mirar modelos realistas de colisiones.)

Movimiento con aceleración constante

Un tipo particular de movimiento que es a la vez relativamente simple y muy importante en la práctica es el movimiento con aceleración constante (ver Figura\(\PageIndex{3}\) nuevamente para ejemplos). Si\(a\) es constante, significa que la velocidad cambia con el tiempo a una velocidad constante, en un número fijo de m/s cada segundo. (Estas son, por cierto, las unidades de aceleración: metros por segundo por segundo, o m/s ².) El cambio en la velocidad a lo largo de un intervalo\(\Delta t\) de tiempo viene dado por

\[ \Delta v = a \Delta t \label{eq:2.4} \]

que también se puede escribir

\[ v=v_{i}+a\left(t-t_{i}\right) \label{eq:2.5} .\]

La ecuación (\ ref {eq:2.5}) es la forma de la función de velocidad (\(v\)como una función de\(t\)) para el movimiento con aceleración constante. Esta, a su vez, tiene que ser la derivada con respecto al tiempo de la función de posición correspondiente. Si conoce derivados simples, entonces, puede verificar que la forma apropiada de la función de posición debe ser

\[ x=x_{i}+v_{i}\left(t-t_{i}\right)+\frac{1}{2} a\left(t-t_{i}\right)^{2} \label{eq:2.6} \]

o en términos de intervalos,

\[ \Delta x=v_{i} \Delta t+\frac{1}{2} a(\Delta t)^{2} \label{eq:2.7} .\]

La mayoría de las veces, la ecuación (\ ref {eq:2.6}) se escribe con la suposición implícita de que el valor inicial de t es cero:

\[ x=x_{i}+v_{i} t+\frac{1}{2} a t^{2} \label{eq:2.8} .\]

Esto es más simple, pero no tan general como la Ecuación (\ ref {eq:2.6}). ¡Siempre asegúrate de saber qué condiciones aplican para cualquier ecuación que decidas usar!

Como puede ver en la Ecuación (\ ref {eq:2.5}), para los intervalos durante los cuales la aceleración es constante, la curva de velocidad vs. tiempo debe ser una línea recta. La figura\(\PageIndex{3}\) ilustra esto. La ecuación (\ ref {eq:2.6}), por otro lado, muestra que para esos mismos intervalos la curva posición vs. tiempo debe ser una (porción de a) parábola, y nuevamente esto se puede ver en la Figura\(\PageIndex{3}\) (a veces, si la aceleración es pequeña, la curvatura de la gráfica puede ser difícil de ver; esto sucede en la Figura \(\PageIndex{3}\)para el intervalo entre\(t\) = 4 s y\(t\) = 5 s).

La observación de que\(v\) -vs-\(t\) es una línea recta cuando la aceleración es constante nos proporciona una manera sencilla de derivar la Ecuación (\ ref {eq:2.7}), cuando se combina con el resultado (del final del capítulo anterior) de que el desplazamiento en un intervalo de tiempo\(\Delta t\) es igual al área bajo la\(t\) curva\(v\) -vs- para ese intervalo de tiempo. En efecto, considere la situación que se muestra en la Figura\(\PageIndex{4}\). El área total debajo del segmento mostrado es igual al área de un rectángulo de base\(\Delta t\) y altura\(v_i\), más el área de un triángulo de base\(\Delta t\) y altura\(v_f − v_i\). Dado que\(v_f − v_i = a\Delta t\), la geometría simple produce inmediatamente la Ecuación (\ ref {eq:2.7}), o su equivalente (\ ref {eq:2.6}).

Figura\(\PageIndex{4}\): Forma gráfica de encontrar el desplazamiento para el movimiento con aceleración constante.

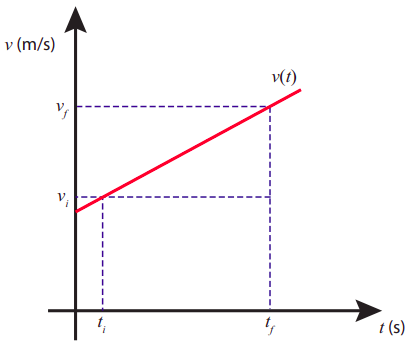
Por último, considere qué sucede si resolvemos la Ecuación (\ ref {eq:2.4})\(\Delta t\) y sustituimos el resultado en (\ ref {eq:2.7}). Obtenemos

\[ \Delta x=\frac{v_{i} \Delta v}{a}+\frac{(\Delta v)^{2}}{2 a} \label{eq:2.9} .\]

Dejando\(\Delta v = v_f − v_i\), un poco de álgebra rinde

\[ v_{f}^{2}-v_{i}^{2}=2 a \Delta x \label{eq:2.10} .\]

Este es un pequeño resultado útil que también se puede ver que sigue, más directamente, de los teoremas trabajo-energía que se introducirán en el Capítulo 7 ¹.

---

¹ De hecho, la ecuación (\ ref {eq:2.10}) resulta ser tan útil que probablemente te encuentres usándola una y otra vez durante este semestre, e incluso podrías sentirte tentado a usarla para problemas relacionados con el movimiento en dos dimensiones. No obstante, a menos que realmente sepas lo que estás haciendo, debes resistir la tentación, ya que es muy fácil usar la Ecuación (\ ref {eq:2.10}) incorrectamente cuando la aceleración y el desplazamiento no se encuentran a lo largo de la misma línea. Deberías usar la forma apropiada de teorema de trabajo-energía en su lugar.

Aceleración como vector

En dos (o más) dimensiones introducimos el vector de aceleración promedio

\[ \vec{a}_{a v}=\frac{\Delta \vec{v}}{\Delta t}=\frac{1}{\Delta t}\left(\vec{v}_{f}-\vec{v}_{i}\right) \label{eq:2.11} \]

cuyos componentes son\(a_{av,x} = \Delta v_x/ \Delta t\), etc. La aceleración instantánea es entonces el vector dado por el límite de la Ecuación (\ ref {eq:2.11}) as\(\Delta t \rightarrow 0\), y sus componentes son, por lo tanto\(a_x = dvx_/dt, a_y = dv_y/dt\),,.

Obsérvese que, dado que\(\vec v_i\) y\(\vec v_f\) en la Ecuación (\ ref {eq:2.11}) son vectores, y tienen que restarse como tales, el vector de aceleración será distinto de cero siempre\(\vec v_i\) y\(\vec v_f\) son diferentes, aunque, por ejemplo, sus magnitudes (que son iguales a la velocidad del objeto) sean las mismas. En otras palabras, se tiene un movimiento acelerado cada vez que cambia la dirección del movimiento, incluso si la velocidad no lo hace.

Mientras estemos trabajando en una dimensión, seguiré la misma convención para la aceleración que introduje para la velocidad en el Capítulo 1: a saber, usaré el símbolo\(a\), sin subíndice, para referirme al componente relevante de la aceleración (\(a_x, a_y,...\)), y no a la magnitud del vector\(\vec a\).

Aceleración en diferentes marcos de referencia

En el Capítulo 1 se vio que la siguiente relación se mantiene entre las velocidades de una partícula P medidas en dos marcos de referencia diferentes, A y B:

\[ \vec{v}_{A P}=\vec{v}_{A B}+\vec{v}_{B P} \label{eq:2.12} .\]

¿Qué pasa con la aceleración? Una ecuación como (\ ref {eq:2.12}) se mantendrá para las velocidades inicial y final, y restándolas obtendremos

\[ \Delta \vec{v}_{A P}=\Delta \vec{v}_{A B}+\Delta \vec{v}_{B P} \label{eq:2.13} .\]

Ahora supongamos que el marco de referencia B se mueve con velocidad constante en relación con el fotograma A. En ese caso\(\vec v_{AB,f} = \vec v_{AB,i}\),, así\(\Delta \vec v_{AB} \) = 0, y luego, dividiendo la Ecuación (\ ref {eq:2.13}) por\(\Delta t\), y tomando el límite\(\Delta t \rightarrow 0\), obtenemos

\[ \left.\vec{a}_{A P}=\vec{a}_{B P} \quad \text { (for constant } \vec{v}_{A B}\right) \label{eq:2.14} .\]

Entonces, si dos fotogramas de referencia se mueven a velocidad constante uno con respecto al otro, los observadores en ambos fotogramas miden la misma aceleración para cualquier objeto que ambos puedan estar rastreando.

El resultado Ecuación (\ ref {eq:2.14}) significa, en particular, que si tenemos un marco inercial entonces cualquier fotograma que se mueva a velocidad constante con relación a él será también inercial, ya que las mediciones de los respectivos observadores coincidirán en que la velocidad de un objeto no cambia (de lo contrario, su aceleración es cero) cuando no hay fuerzas que actúen sobre ello. Por el contrario, una trama acelerada no será una trama inercial, porque la ecuación (\ ref {eq:2.14}) no se mantendrá. Esto concuerda con los ejemplos que mencioné en la Sección 2.1 (el avión que rebota, el automóvil que se detiene). Otro ejemplo de un cuadro no inercial sería un automóvil dando la vuelta a una curva, aunque vaya a velocidad constante, ya que, como acabo de señalar anteriormente, se trata también de un sistema acelerado. Esto se confirma por el hecho de que los objetos en un automóvil de este tipo tienden a moverse —con relación al automóvil— hacia el exterior de la curva, a pesar de que ninguna fuerza real está actuando sobre ellos.