9.5: Estática
- Page ID
- 128167
La estática es la rama de la mecánica que se ocupa de las fuerzas y tensiones 5 necesarias para mantener un sistema en reposo, en un equilibrio estable, para que no se mueva, se doble o colapse. Es, obviamente, extremadamente importante en ingeniería (particularmente en ingeniería mecánica). En un curso introductorio a la física, solo podemos tratarlo a un nivel muy elemental, ignorando por completo la deformación de objetos extendidos como tablones y vigas (y las tensiones asociadas), y simplemente imponiendo dos condiciones simples para el equilibrio estático: primero, la fuerza neta (externa) en el sistema debe ser cero, para asegurarse de que su centro de masa permanezca en reposo; y segundo, el par neto (externo) en el sistema también debe ser cero, para que no gire. Estas condiciones pueden expresarse simbólicamente como
\ begin {align}
\ sum\ vec {F} _ {e x t} =0\ nonumber\
\ sum\ vec {\ tau} _ {e x t} =0\ label {eq:9.27}
\ end {align}
Puede preguntar sobre qué punto se deben calcular los pares. La respuesta es que, mientras se cumpla la primera condición (la suma de las fuerzas es cero), ¡no importa! La prueba es simple, pero eres bienvenido a omitirla si no te interesa.
Supongamos que tiene dos puntos, A y B, alrededor de los cuales calcular los pares. Que\(\vec r_{A1}\),\(\vec r_{A2}\),... sean los vectores de posición de los puntos de aplicación de las fuerzas\(\vec F_{1}\),\(\vec F_{2}\)..., relativo al punto A, y\(\vec r_{B1}\),\(\vec r_{B2}\),..., lo mismo, pero relativo al punto B. Si vas todo el camino de regreso a la Figura 1.3.1 (en el Capítulo 1), se puede ver que estos vectores solo difieren del primer conjunto por el vector constante único\(\vec r_{AB}\) que da la posición del punto B con respecto al punto A:\(\vec{r}_{A 1}=\vec{r}_{A B}+\vec{r}_{B 1}\), etc. entonces, para la suma de pares alrededor de A tenemos
\ begin {align}
\ vec {r} _ {A 1}\ veces\ vec {F} _ {1} +\ vec {r} _ {A 2}\ veces\ vec {F} _ {2} +\ lpuntos &=\ izquierda (\ vec {r} _ {A B} +\ vec {r} _ {B} _ {B 1}\ derecha)\ veces\ vec {F}} _ {1} +\ izquierda (\ vec {r} _ {A B} +\ vec {r} _ {A 2}\ derecha)\ veces\ vec {F} _ {2} +\ ldots\ nonumber\\
&=\ vec {r} _ {A B}\ veces\ izquierda (\ vec {F} _ {1} +\ vec {F} _ {2}\ lpuntos\ derecha) +\ vec {r} _ {B 1}\ veces\ vec {F} _ {1} +\ vec {r} _ {B 2}\ veces\ vec {F} _ {2} +\ lpuntos\ etiqueta {eq:9.28}
\ end {align}
El primer término en la última línea es cero si la suma de todas las fuerzas es cero, y lo que queda es la suma de todos los pares alrededor de B. Esto, efectivamente, para los blemas estáticos pro 1, siempre y cuando estemos haciendo cumplir\(\sum \vec{F}_{e x t}=0\), no importa en qué punto elegimos calcular el par. Una elección natural es el centro de masa del sistema, ya que ese suele ser un punto de alta simetría, pero también podemos elegir un punto donde haya muchas fuerzas aplicadas, y así deshacernos de ellas rápidamente (ya que sus pares sobre ese punto serán cero).
La forma en que todo esto funciona probablemente se ilustra mejor con un ejemplo. La figura\(\PageIndex{1}\) muestra una clásica, una escalera apoyada contra una pared. El boceto de la izquierda muestra los ángulos y dimensiones involucrados, mientras que el diagrama de cuerpo libre extendido adecuado, que muestra todas las fuerzas y sus puntos de aplicación, está a la derecha.
El número mínimo de fuerzas necesarias para equilibrar el sistema es de cuatro: el peso de la escalera (que actúa en el centro de masa), una fuerza normal desde el suelo, otra fuerza normal de la pared y una fuerza de fricción estática desde el suelo que impide que la escalera se deslice. En la vida real también debe haber una fuerza de fricción estática desde la pared, apuntando hacia arriba (también para evitar el deslizamiento); y, por supuesto, si hay una persona en la escalera ejercerá una fuerza adicional hacia abajo sobre ella (igual a su peso), aplicada en cualquier momento en que esté de pie. No voy a considerar ninguna de estas complicaciones, sólo para mantener el ejemplo simple, sino que podrían tratarse exactamente de la misma manera.
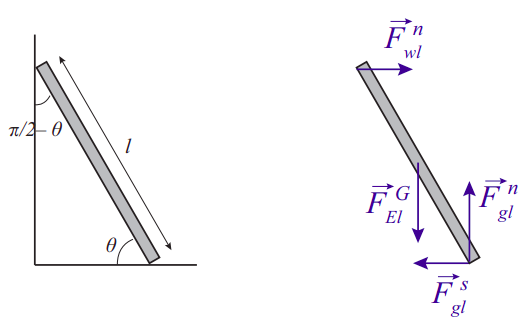
Con la convención de que una cantidad vectorial sin una flecha en la parte superior representa la magnitud de ese vector, la ecuación para el equilibrio de las fuerzas verticales dice
\[ F_{g l}^{N}-m g=0 \label{eq:9.29} .\]
Para las fuerzas horizontales, tenemos
\[ F_{w l}^{N}-F_{g l}^{s}=0 \label{eq:9.30} .\]
Entonces, tomando pares alrededor del punto donde la escalera está en contacto con el suelo, ninguna de las dos fuerzas aplicadas en ese punto contribuirá, y la condición de que la suma de los pares sea igual a cero se convierte en
\[ F_{w l}^{N} l \sin \theta-m g \frac{l}{2} \cos \theta=0 \label{eq:9.31} .\]
Esto se debe a que el ángulo realizado por la fuerza de gravedad con el vector de posición de su punto de aplicación es\(\frac{\pi}{2}-\theta\), y\(\sin \left(\frac{\pi}{2}-\theta\right)=\cos \theta\). De la primera ecuación obtenemos eso\(F_{g l}^{N}=m g\); a partir de la segunda obtenemos que la otra fuerza normal,\(F_{w l}^{N}=F_{g l}^{s}\). Si sustituimos esto en (\ ref {eq:9.31}), y cancelamos\(l\), la longitud de la escalera, obtenemos la condición
\[ F_{g l}^{s}=\frac{1}{2} m g \cot \theta \label{eq:9.32} .\]
Pero la fuerza de fricción estática no puede exceder\(\mu_{s} F_{g l}^{N}=\mu_{s} m g\), por lo que, ajustando el lado derecho de (\ ref {eq:9.32}) para que sea menor o igual a\(\mu_s mg\), y cancelando el factor común mg, obtenemos la condición
\[ \cot \theta \leq 2 \mu_{s}, \quad \text { or } \quad \tan \theta \geq \frac{1}{2 \mu_{s}} \label{eq:9.33} \]
para el ángulo \(\theta\)mínimo en el que podemos inclinar la escalera antes de que se resbale y caiga.
5 Una “tensión” es una fuerza “distribuida” en un objeto extendido, que varía continuamente de un punto a otro.