9.8: Ejemplos

Este fue un capítulo largo, en parte porque contiene una serie de ejemplos útiles elaborados; ¡así que por favor asegúrate de no pasarlos por alto! La sección 9.2 mostró un par de ejemplos de problemas que pueden resolverse utilizando la conservación del momento angular. La Sección 9.3 le muestra cómo configurar y resolver las ecuaciones de equilibrio para una escalera inclinada, que es el arquetipo de todos los problemas estáticos; y la Sección 9.4 también resuelve para usted el problema de un objeto genérico rodando por un plano inclinado.

El primer par de ejemplos adicionales en esta sección muestran que tienes que configurar y resolver las ecuaciones de movimiento para sistemas algo más complicados, y debes estudiarlos cuidadosamente.

Ejemplo\(\PageIndex{1}\): Torques and forces on the wheels of an accelerating bicycle

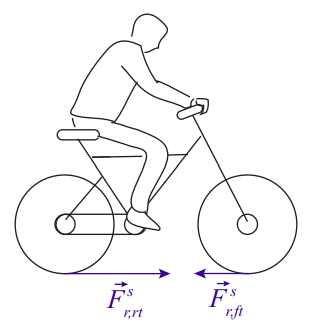
Considera una bicicleta acelerada. El piloto ejerce un par sobre los pedales, el cual es transmitido a la rueda trasera por la cadena (posiblemente amplificado por los engranajes, etc.). ¿Cómo se relaciona este par de “accionamiento” en la rueda trasera (llámalo\(\tau_d\)) con la aceleración final del centro de masa de la bicicleta?

Solución

Primero tenemos que averiguar cuántas fuerzas externas, como mínimo, tenemos que lidiar. A medida que la bicicleta acelera, suceden dos cosas: las ruedas (ambas ruedas) giran más rápido, por lo que debe haber un par neto (en el sentido de las agujas del reloj en la imagen, si la bicicleta está acelerando hacia la derecha) en cada rueda; y el centro de masa del sistema acelera, por lo que debe haber una fuerza externa neta sobre el todo el sistema. El sistema solo está en contacto con la carretera, y así, mientras no ocurra ningún deslizamiento, la única fuente externa de pares o fuerzas sobre las ruedas tiene que ser la fuerza de fricción estática entre las llantas y la carretera.

Para la rueda delantera, esta es de hecho la única fuerza externa, y la única fuerza de cualquier tipo que ejerce un par sobre esa rueda (hay fuerzas que actúan en el eje, pero no ejercen torque alrededor del eje). Dado que el par tiene que ser en el sentido de las agujas del reloj, entonces, la fuerza de fricción estática sobre la rueda delantera, aplicada como está en el punto de contacto con la carretera, debe apuntar hacia atrás, es decir, opuesta a la dirección del movimiento. Obtenemos entonces una ecuación de movimiento (del tipo (9.4.7)) para esa rueda:

\[ -F_{r, f t}^{s} R=I \alpha \label{eq:9.44} \]

donde el subíndice “ft” significa “neumático delantero”, y se supone que la rueda tiene un radio\(R\) y un momento de inercia\(I\).

Para la rueda trasera, tenemos el “par motor”\(\tau_d\), ejercido por la cadena, y otro par ejercido por la fuerza de fricción estática,\(\vec F^s_{r,rt}\), entre ese neumático y la carretera. No obstante, ahora la fuerza\(\vec F^s_{r,rt}\) necesita señalar hacia adelante. Esto se debe a que la fuerza externa neta en todo el sistema bicicle-rider es\(\vec{F}_{r, r t}^{s}+\vec{F}_{r, f t}^{s}\), y eso tiene que apuntar hacia adelante, o el centro de masa nunca podría acelerar en esa dirección. Ya que hemos establecido que\(F^s_{r,f t}\) tiene que apuntar hacia atrás, se deduce que\(F^s_{r,rt}\) necesita ser más grande, y en la dirección hacia adelante. Esto significa que obtenemos, para el centro de aceleración de masa, la ecuación (\(F_{net} = M a_{cm}\))

\[ F_{r, r t}^{s}-F_{r, f t}^{s}=M a_{c m} \label{eq:9.45} \]

y para la rueda trasera, la ecuación de par

\[ F_{r, r t}^{s} R-\tau_{d}=I \alpha \label{eq:9.46} .\]

Estoy siguiendo la convención de que los pares en sentido horario son negativos, y también que un símbolo de fuerza sin flecha en la parte superior representa la magnitud de la fuerza. Si una aceleración angular en el sentido de las agujas del reloj es igualmente negativa, la condición de rodar sin deslizamiento [Ecuación (9.6.4)] debe escribirse como

\[ a_{cm} = -R \alpha \label{eq:9.47} .\]

Estas son todas las ecuaciones con las que necesitamos relacionar la aceleración\(\tau_d\). Podemos comenzar resolviendo (\ ref {eq:9.44})\(F^s_{r,f t}\) y sustituyendo en (\ ref {eq:9.45}), luego resolviendo igualmente (\ ref {eq:9.46})\(F^s_{r,rt}\) y sustituyendo en (\ ref {eq:9.45}). El resultado es

\[ \frac{I \alpha+\tau_{d}}{R}+\frac{I \alpha}{R}=M a_{c m} \label{eq:9.48} \]

luego usa Eq (\ ref {eq:9.47}) para escribir\(\alpha = −a_{cm}/R\) y resolver para\(a_{cm}\):

\[ a_{c m}=\frac{\tau_{d}}{M R+2 I / R} \label{eq:9.49} \]

Ejemplo\(\PageIndex{2}\): Blocks connected by rope over a pulley with non-zero mass

Consideremos nuevamente la configuración ilustrada en la Figura 6.3.1, pero ahora supongamos que la polea tiene masa\(M\) y radio\(R\). Para simplificar, deje fuera la fuerza de fricción. ¿Cuál es ahora la aceleración del sistema?

Solución

La siguiente figura muestra la configuración, además de diagramas de cuerpo libre para los dos bloques (las fuerzas verticales en el bloque 1 se han dejado fuera para evitar abarrotar la figura, ya que aquí no son relevantes), y un diagrama extendido de cuerpo libre para la polea. (Se puede ver en el diagrama de poleas que tiene que haber otra fuerza actuando sobre ella, para equilibrar las dos fuerzas mostradas. Esta sería una fuerza de contacto en el eje, dirigida hacia arriba y hacia la izquierda. Si esto fuera un problema de estática, tendría que incluirlo, pero como no ejerce un par alrededor del eje de rotación, no contribuye a la dinámica del sistema, por lo que también lo he dejado fuera).

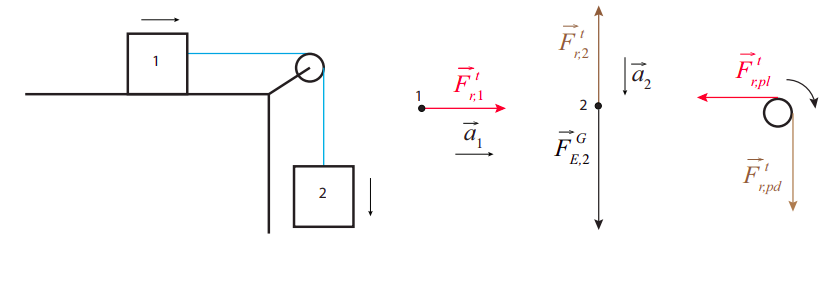
La nueva característica clave de este problema es que la tensión en la cuerda tiene que tener diferentes valores a cada lado de la polea, ya que tiene que haber un par neto en la polea. Por lo tanto, la fuerza hacia la izquierda sobre la polea (\(F^t_{r,pl}\)) tiene que ser menor que la fuerza hacia abajo (\(F^t_{r,pd}\)).

Por otro lado, siempre y cuando la masa de la cuerda sea insignificante, seguirá siendo el caso de que la parte horizontal de la cuerda tire con igual fuerza sobre el bloque 1 y sobre la polea, y de manera similar la parte vertical de la cuerda tirará con igual fuerza sobre la polea y sobre el bloque 2. (Para que este punto sea más claro, tengo “codificadas por colores” estas fuerzas coincidentes en la figura). Esto significa que podemos escribir\(F^t_{r,pl} = F^t_{r,1}\) y\(F^t_{r,pd} = F^t_{r,2}\), y escribir la ecuación de par (9.4.7) para la polea como

\[ F_{r, 1}^{t} R-F_{r, 2}^{t} R=I \alpha \label{eq:9.50} .\]

También tenemos\(F = ma\) para cada bloque:

\[ F_{r, 1}^{t}=m_{1} a \label{eq:9.51} \]

\[ F_{r, 2}^{t}-m_{2} g=-m_{2} a \label{eq:9.52} \]

donde he llevado\(a\) a estar\(a = |\vec{a}_1| = |\vec{a}_2|\). La condición de rodar sin resbalar, Ecuación (9.6.4), aplicada a la polea, da entonces

\[ -R \alpha = a \label{eq:9.53} \]

ya que, en la situación mostrada,\(\alpha\) será negativa, y se\(a\) ha definido como positiva. Sustitución de Eqs. (\ ref {eq:9.51}), (\ ref {eq:9.52}), y (\ ref {eq:9.53}) en (\ ref {eq:9.50}), obtenemos

\[ m_{1} a R-\left(m_{2} g-m_{2} a\right) R=-\frac{I a}{R} \label{eq:9.54} \]

que se resuelve fácilmente para\(a\):

\[ a=\frac{m_{2} g}{m_{1}+m_{2}+I / R^{2}} \label{eq:9.55} .\]

Si nos fijamos en la estructura de esta ecuación, todo tiene sentido. El numerador es la fuerza de gravedad sobre el bloque 2, que es, en última instancia, la fuerza responsable de poner todo en movimiento. El denominador es, esencialmente, la inercia del sistema: inercia ordinaria para los bloques, e inercia rotacional para la polea. Obsérvese además que, si tratamos la polea como un disco plano y homogéneo de masa\(M\)\(I = \frac{1}{2}MR^2\), entonces, y el denominador de (\ ref {eq:9.55}) se vuelve justo\(m_1 + m_2 + M/2\).