9.9: Ejercicios

Ejercicio\(\PageIndex{1}\)

Una patinadora sobre hielo tiene un momento de inercia igual a 1.9 kg·m ² cuando gira con los brazos estirados, a razón de 2 revoluciones por segundo. Luego trae sus brazos, alineados con su eje de rotación, por lo que su momento de inercia se convierte en 1.1 kg·m ².

1. ¿Cuál es su nueva velocidad angular? (Puedes usar radianes por segundo, o revoluciones por segundo si lo prefieres.)
2. ¿Cuál es el cambio en su energía cinética?
3. ¿De dónde viene esta energía?

Ejercicio\(\PageIndex{2}\)

Dos discos idénticos, cada uno de inercia \(m\), están conectados a una varilla de longitud\(2r\) e inercia insignificante que gira alrededor de su centro (es decir, hay algún tipo de pasador a través de su centro, alrededor del cual puede girar sin fricción). Un tercer disco de inercia\(m/2\) golpea uno de los discos conectados perpendicular a la varilla con una velocidad\(v_i\). Supongamos que la colisión es elástica.

1. Dibuja un diagrama de la situación, etiquetando claramente la dirección de vi y en qué dirección rotarán los discos conectados.
2. ¿Se conserva el impulso total del sistema (los tres discos y la varilla) a lo largo de la interacción? ¿Por qué? ¿Está aislado el sistema, o se puede identificar una fuerza externa que actúe sobre él?
3. ¿Se conserva la energía cinética total del sistema? ¿Por qué? Si encontró una fuerza externa en la parte (b), explique por qué funciona o no funciona en el sistema.
4. ¿Se conserva el momento angular total del sistema? ¿Por qué? Si encontró una fuerza externa en la parte (b), explique por qué ejerce o no un par sobre el sistema.
5. Anote una expresión para el momento de inercia ( inercia rotacional) del sistema formado por los discos conectados.
6. Con base en todo lo anterior, anotar ecuaciones que expresen la conservación de las dos cantidades que de hecho se conservan. Estas ecuaciones deben involucrar únicamente los datos dados (masas, longitud de la varilla); las velocidades inicial y final\(v_f\),\(v_i\) y, del disco libre; y\(\omega\), la velocidad angular de los discos conectados después de la colisión. (Supongamos que la velocidad final del disco libre se encuentra a lo largo de la misma línea que su velocidad inicial, es decir, no rebota en algún ángulo aleatorio).

Ejercicio\(\PageIndex{3}\)

Una tabla de longitud\(l\) = 2 m está articulada en un extremo a una pared. El otro extremo está siendo apoyado (temporalmente) por un trabajador que lo sostiene con la mano, manteniendo la tabla horizontal. El tablón tiene una masa de 20 kg, y también hay una caja de herramientas de masa de 5 kg sentada sobre ella, a 50 cm de distancia del trabajador (a 1.5 m de la pared).

1. Dibuje un diagrama de cuerpo libre y un diagrama de cuerpo libre extendido para la tabla.
2. ¿Cuáles son las magnitudes de (1) la fuerza hacia arriba ejercida por el trabajador sobre la tabla y (2) la fuerza en la bisagra?
3. Si el trabajador soltara la tabla, ¿cuál sería su aceleración angular cuando empieza a balancearse hacia abajo? El momento de inercia es\(I = \frac{1}{3}Ml^2\). (Nota: supongamos que la caja de herramientas deja de presionar la tabla inmediatamente. Esta es una buena aproximación, como verá a continuación.)
4. Considera un punto en el tablón ubicado inmediatamente debajo de la caja de herramientas. A medida que la tabla se balancea, este punto se mueve en un círculo de radio 1.5 m. ¿Cuál es su aceleración lineal (tangencial) a medida que comienza a bajar, y cómo se compara con la aceleración de la gravedad?

Ejercicio\(\PageIndex{4}\)

Una esfera sólida de radio 5 cm y masa 0.2 kg está rodando sin deslizarse, sobre terreno nivelado, a una velocidad constante de 0.5 m/s, se dirige hacia una rampa que hace un ángulo de 30\(^{\circ}\) con la horizontal.

1. ¿Cuál es la velocidad angular de la esfera, en radianes por segundo?
2. Si el momento de inercia de una esfera sólida y homogénea es\ (I =\ frac {2} {5} mR^2\), ¿cuál es el momento angular inicial de esta esfera?
3. ¿Cuál es la energía cinética traslacional de la esfera?
4. ¿Cuál es su energía cinética rotacional?
5. ¿Qué tan alto (verticalmente) se elevará la esfera a medida que sube por la rampa, aún rodando sin resbalar, antes de que se detenga y dé la vuelta?
6. Dibuja un diagrama extendido de cuerpo libre para la esfera a medida que rueda por la rampa. En el diagrama, indique la dirección de rotación, y la dirección de la aceleración del centro de masa.
7. Refiriéndose al diagrama extendido de cuerpo libre en la pregunta anterior, ¿qué fuerza es responsable del cambio en el momento angular de la esfera a medida que rueda por la rampa? Explique brevemente: ¿Por qué esa fuerza y no otra? ¿La dirección que ha asumido para esta fuerza concuerda con el par que tiene que proporcionar? (Si no, ¡será mejor que regrese y arregle eso ahora mismo!)
8. Calcular la aceleración de la esfera a medida que rueda por la rampa.

Ejercicio\(\PageIndex{5}\)

Una cuerda muy ligera e inextensible se envuelve alrededor de un carrete cilíndrico. El extremo de la cuerda se mantiene fijo, y el carrete se suelta para que comience a caer, a medida que la cuerda se desenrolla. Debido a que el carrete es básicamente hueco, puedes tomar su momento de inercia para ser\(I = mR^2\).

1. Dibuja un diagrama extendido de cuerpo libre para el carrete a medida que se desenrolla.
2. Encuentra la aceleración lineal del carrete a medida que acelera hacia el suelo.
3. Deje que la masa de la bobina sea de 0.1 kg. ¿Cuál es su energía cinética traslacional después de que ha caído 0.5 s?
4. ¿Cuál es su energía cinética rotacional en ese momento?
5. ¿Cuál es la tensión en la cuerda? ¿Esto cambia a medida que cae el carrete? (Recuerda que la masa de la cuerda es insignificante).
6. Si el radio del carrete es de 3 cm, ¿cuál es la magnitud del par (alrededor del centro de masa) ejercido por la tensión?

Ejercicio\(\PageIndex{6}\)

Una tabla de 20 kg de longitud\(l\) = 4 m se soporta en ambos extremos como se muestra en la figura. Un hombre de 60 kg está parado a una\(l/3\) distancia del extremo derecho de la tabla.

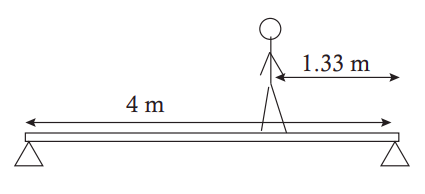
1. Dibuje un diagrama extendido de cuerpo libre para la tabla. Trate de obtener la escala de las fuerzas al menos cualitativamente correcta.
2. Encuentra la fuerza hacia arriba sobre la tabla ejercida por cada uno de los dos soportes.