10.4: Ejemplos

Ejemplo\(\PageIndex{1}\): Orbital dynamics

En los primeros días del vuelo espacial, los astronautas a veces mencionaban los aspectos contrarios a la intuición del vuelo orbital. Por ejemplo, si, desde una órbita circular alrededor de la Tierra, querían moverse a una órbita inferior, la manera de hacerlo era ralentizar su cápsula (disparando un propulsor en la dirección opuesta a su movimiento). Esto los llevaría a una órbita inferior, pero entonces la cápsula comenzaría a acelerar, por sí sola.

Utilice los conceptos introducidos en este capítulo para explicar lo que sucede en este escenario. Dejado\(R\) ser el radio de la órbita inicial. Por simplicidad, suponga que el empuje está encendido solo por muy poco tiempo, por lo que puede descuidar el movimiento de la cápsula durante este tiempo. En otras palabras, trátelo como una reducción instantánea de la velocidad, y discuta:

1. ¿Qué sucede con el potencial y la energía cinética del sistema, y el momento angular?
2. ¿La nueva órbita es circular o elíptica? ¿Cómo lo sabes? ¿Cuál es la nueva órbita\(r_{max}\) (distancia máxima al centro de la Tierra)?
3. ¿Por qué la cápsula acelera en su nueva órbita?
4. Si la nueva órbita no es circular, ¿qué necesitarían hacer los astronautas para que así sea? (Sin acercarnos más a la Tierra, es decir, mantener\(r_{min}\) lo mismo.)

Asegúrate de dibujar un diagrama de la situación. Hazlo lo más preciso que puedas.

Solución

(a) Bajo el supuesto de que la cápsula apenas cambia de posición durante el disparo del propulsor, la energía potencial del sistema, que es igual a\ (U^G = −GMm/R\), no cambiará:\(U^G_f = U^G_i\).

La energía cinética, por otro lado, bajará, ya que la velocidad de la cápsula se reduce:\ (K_f < K_i\). De ahí que la energía mecánica total del sistema,\ (E = K + U^G\), disminuirá:\(E_f < E_i\).

El momento angular irá a la baja, ya que v baja.

(b) La nueva órbita tiene que ser elíptica, ya que para tener una órbita circular a distancia se\(R\) requiere una velocidad precisa (dada justo debajo de la Ecuación (10.1.11\(v=\sqrt{G M / R}\)) por), y ahora hemos cambiado eso.

No obstante, dado que la órbita debe seguir siendo una curva cerrada, contendrá el punto de partida, que es, por nuestra suposición, a una\(R\) distancia de la Tierra. Además, si la dirección del vector de velocidad no cambia como resultado del disparo del propulsor (solo\(v\) se supone que cambia la magnitud de), se deduce que en este punto los vectores de velocidad y posición son perpendiculares. Para una órbita circular, este es el caso en todas partes. Para una órbita elíptica, esto solo es cierto en los dos puntos extremos etiquetados P y A en la Figura 10.1.3 (el perigeo y el apogeo, respectivamente). Entonces, la posición inicial de la cápsula se convierte ya sea en el perigeo o en el apogeo de la nueva órbita. ¿Cuál es?

Para obtener la respuesta, recordemos que encontramos en (a) que la energía mecánica total\(E\) ha bajado. Pero, como\(E\) es un número negativo, esto quiere decir que la magnitud de\(E\) ha subido. Entonces, en la fórmula (10.1.14),

\ [E=-\ frac {G M m} {2 a} \ nonumber\]

el eje semimajor\(a\) debió haber bajado. Para la órbita circular original, teníamos\ (a = R\); ahora, debemos tener\(a < R\). Esto significa que el punto de partida, a una\(R\) distancia del (centro de la) Tierra, no puede ser el perigeo (el punto de aproximación más cercano), ya que en ese punto\(r = r_{min}\), y siempre\(r_{min}\) es menor que \(a\) (vuelva a consultar la Figura 10.1.3, o Eqs. (10.1.12)). En cambio, el punto de partida tiene que ser el apogeo de la nueva órbita, y por lo tanto la distancia en ese punto es también la distancia máxima:\(r_{max} = R\).

(c) La cápsula se acelera en su nueva órbita porque, como acabamos de ver, comienza tan lejos de la Tierra como va a llegar; por lo tanto, a medida que se mueva comenzará a acercarse a la Tierra, y sabemos por la segunda ley de Kepler que a medida que se acerca tiene que acelerar. (También se puede decir que, a medida que se acerque, la energía potencial gravitacional del sistema bajará, y por lo tanto su energía cinética debe aumentar).

d) La forma más fácil de cambiar la nueva órbita a una órbita circular con radio\(r_{min}\) sería realizar otra maniobra de reducción de velocidad, pero esta vez en perigeo. En perigeo, la distancia a la Tierra ya está\(r_{min}\), que es lo que quieres que sea, pero la cápsula se mueve demasiado rápido para permanecer en una órbita circular (dicho de otra manera, la fuerza gravitacional de la Tierra en ese punto es demasiado débil para doblar la órbita en un círculo): por eso es que finalmente termina “sobrepasando” la Tierra en el otro lado. Reducir\(v\) se reducirá aún más\(E\) y, por el mismo argumento anterior, resultará en una órbita con una menor\(a\), que es lo que se quiere (ya que, por el momento,\ (a > r_ {min}\), y quieres que lo nuevo\(a\) sea igual a \(r_{min}\)).

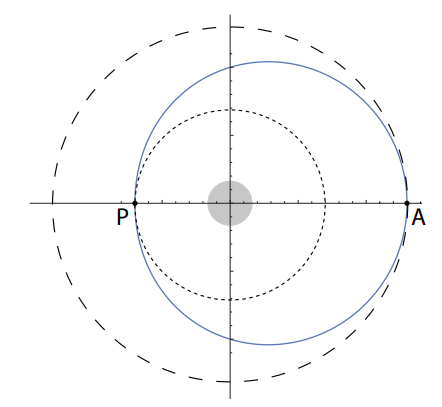
El diagrama de la situación está arriba (página anterior). El círculo de trazos largos es la órbita original; la línea continua es la órbita elíptica resultante de la reducción de velocidad en el punto A; el círculo de trazos cortos es la órbita circular que resultaría de otra reducción de velocidad en el punto P. Nota: el tamaño de las órbitas es muy exagerado comparado a los que estaban en los primeros vuelos espaciales, ¡que estaban mucho más cerca de la Tierra!

La forma de dibujar este tipo de figura es dibujar primero una elipse precisa, asegurándote de saber dónde está el foco; luego dibujar los círculos centrados en el foco y tocar la elipse en los puntos correctos. La ecuación de una elipse en forma polar, con el origen en un foco, es\ (r = a + ae \ cos\ phi\).

Ejemplo\(\PageIndex{2}\): datos orbitales de observaciones- cometa Halley

El cometa Halley sigue una órbita elíptica alrededor del sol. En su aproximación más cercana, se encuentra a una distancia de 0.59 UA del sol (una unidad astronómica, AU, se define como la distancia promedio de la tierra al sol: 1 AU = 1.496 × 10 ¹¹ m), y se mueve a 5.4 × 10 ⁴ m/s Sabemos que su periodo es de aproximadamente 76 años. Ignorando las fuerzas ejercidas sobre el cometa por los otros objetos del sistema solar (una aproximación bastante aproximada):

1. Utilice la ley Kepler apropiada para inferir el valor de a (el eje semimajor) para la órbita del cometa.
2. ¿Cuál es la excentricidad de la órbita del cometa?
3. Utilizando el resultado en (a) y la conservación del momento angular, encuentra la velocidad del cometa en el afelio (el punto en su órbita cuando está más alejado del sol).

Solución

a) La “ley Kepler apropiada” aquí es la tercera. Para dos objetos cualesquiera que orbiten, por ejemplo, el sol, el cuadrado de sus periodos orbitales es proporcional al cubo de los ejes semimajores de sus órbitas, con la misma constante de proporcionalidad (\(4\pi/GM_{sun}\); ver Ecuación (10.1.18)). Ni siquiera necesitamos calcular la constante de proporcionalidad; podemos dividir la ecuación para el cometa Halley por la ecuación para la tierra, y obtener

\ [\ frac {T_ {\ texto {Halley }} ^ {2}} {T_ {\ texto {tierra}} ^ {2}} =\ frac {a_ {\ texto {Halley }} ^ {3}} {a_ {\ texto {tierra}} ^ {3}}\ etiqueta {eq:10.21}\]

donde\(T^2_{earth}\) = 1 año ², y\(a^3_{earth}\) = 1 AU ³, así que obtenemos inmediatamente

\ [a_ {\ text {Halley }} =\ izquierda (76^ {2}\ derecha) ^ {1/3}\ mathrm {AU} =17.9\:\ mathrm {AU} \ label {eq:10.22}\]

(b) Podemos obtener este de una mirada a la Figura 10.1.3: el producto\(ea\), más la distancia mínima entre el cometa y el sol (0.59 AU) es igual a\(a\). (Esto es justo lo que dice también la segunda de las ecuaciones (10.1.12).). Así que tenemos

\ [e=\ frac {a-r_ {\ min }} {a} =1-\ frac {r_ {\ min}} {a} =1-\ frac {0.59} {17.9} =0.967 \ label {eq:10.23}\]

Tenga en cuenta que ni siquiera tuvimos que convertir AU a kilómetros. En este tipo de problemas, particularmente, donde hay que manipular números muy grandes, realmente vale la pena hacer todos los cálculos simbólicamente y no sustituir los números hasta el final, para ver si algo se cancela, y para evitar errores al copiar números grandes forman uno línea a la siguiente; y a veces, como aquí, ¡ni siquiera tienes que convertir a otras unidades!

(c) En el punto de aproximación más cercano (perihelio), la velocidad y el vector de posición del cometa son perpendiculares, por lo que la magnitud del momento angular del cometa es igual a\(L = mrv\). Lo mismo ocurre en el punto más lejano de la órbita (afelio), y como el momento angular se conserva para el problema Kepler, podemos escribir

\ [m r_ {\ min} v_ {\ max} =m r_ {\ max} v_ {\ min}\ etiqueta {eq:10.24}\]

(la razón de esta elección de subíndices es que sabemos que cuando\(r\) es máximo,\(v\) es mínimo, y viceversa). Resolviendo para\(v_{min}\), la velocidad al afelio, obtenemos

\ [v_ {\ min} =\ frac {r_ {\ min }} {r_ {\ max}} v_ {\ max} =\ frac {r_ {\ min}} {2 a-r_ {\ min}} v_ {\ max } =\ frac {0.59} {2\ cdot 17.9-0.59} 5.4\ veces 10^ {4} \:\ frac {\ mathrm {m}} {\ mathrm {s}} =905\: \ frac {\ mathrm {m}} {\ mathrm {s}}\ label {eq:10.25}.\]

Aquí nuevamente la ecuación que utilicé para encontrar\(r_{max}\) puede derivarse directamente de la Figura 10.1.3 (y también es una de las ecuaciones (10.1.12): \(r_{min} + r_{max} = 2a\)). Una vez más, pude usar AU en todo momento, ya que las unidades de distancia cancelan en la fracción \(r_{min}/r_{max}\).