10.5: Temas Avanzados

Fuerzas mareales

A lo largo de este capítulo hemos tratado los objetos que interactúan gravitacionalmente como si fueran partículas, es decir, como si fueran indeformables y su forma y orientación relativa no importaran. Sin embargo, estas condiciones nunca se realizan del todo en la vida real. Algunos planetas, como nuestra propia Tierra, son particularmente susceptibles a la deformación, debido a la gran cantidad de materia fluida en su superficie, e incluso los planetas rocosos y lunas son sensibles a las fuerzas mareales, que son las diferencias en la atracción gravitacional del atractor central en diferentes partes del objeto considerado.

Si miras hacia atrás en la Figura 10.1.1, por ejemplo, es fácil ver que la luna debe estar tirando más fuertemente del lado de la Tierra que está más cerca de ella (el lado izquierdo, en esa imagen) que en el lado más lejano. Esto es, por supuesto, porque la fuerza de gravedad depende de la distancia entre los objetos que interactúan, y es más fuerte cuando los objetos están más cerca. Se puede calcular fácilmente que la fuerza por la luna sobre un volumen dado de la Tierra (digamos, un metro cúbico) es aproximadamente 7% más fuerte en el lado cercano que en el lado lejano. Un objeto deformable sujeto a tal par de fuerzas se estirará naturalmente en la dirección del tirón: en el caso de la Tierra, este “estiramiento” afecta principalmente al agua en los océanos que cubren la mayor parte de la superficie, resultando en dos “bultos mareales” que dan cuenta del conocido fenómeno de mareas: a medida que la tierra gira alrededor de su eje, cada punto de la superficie pasa por uno de los bultos una vez al día, resultando en dos mareas altas cada día (y, en medio, un nivel de agua comparativamente más bajo, o marea baja, dos veces al día también). ⁵

Para muchos objetos del sistema solar, este estiramiento de las mareas ha resultado, a lo largo de millones de años, en una deformación permanente. Las fuerzas mareales de la Tierra en la luna son más débiles que las de la luna en la Tierra (ya que la luna es mucho más pequeña, la diferencia entre la atracción de la Tierra en el lado cercano y lejano de la luna es menor de 1.5%), pero en un momento en que la luna era más maleable que en la actualidad, bastaba para producir un elongación a lo largo del eje Tierra-Luna que ahora está prácticamente congelado en su lugar.

Una vez que un satélite (usaré el término genéricamente para referirme ya sea a un planeta que orbita al sol, o a una luna que orbita un planeta) se deforme permanentemente, puede ocurrir un nuevo fenómeno, conocido como bloqueo de mareas. Supongamos que el satélite gira alrededor de su propio eje, además de orbitar alrededor del cuerpo primario. Como puede ver en la siguiente figura, si la rotación es demasiado rápida, las fuerzas gravitacionales del primario resultarán en un par neto en el satélite que tenderá a ralentizar su rotación; a la inversa, si está girando demasiado lentamente, el par tenderá a acelerar la rotación. Una situación sin par sólo ocurrirá cuando el periodo de rotación del satélite coincida exactamente con su periodo orbital, de manera que siempre muestre el mismo lado al cuerpo primario. Esta es la situación con la luna de la Tierra, y de hecho para la mayoría de las lunas mayores de los planetas gigantes.

Figura\(\PageIndex{1}\): Luna alargada que gira alrededor de un planeta en órbita en el sentido de las agujas del reloj, y al mismo tiempo que gira en sentido horario alrededor de un eje a través de su centro. En (a), la rotación es demasiado rápida, lo que resulta en un “par mareario” en sentido contrario a las agujas del reloj. En (b), la rotación es demasiado lenta, y el “par mareario” es en sentido horario. En ambos casos, el par se debe a la desalineación de la luna, y a que la fuerza gravitacional en su lado cercano es más fuerte que en su lado lejano, como lo muestran los vectores de fuerza azules.

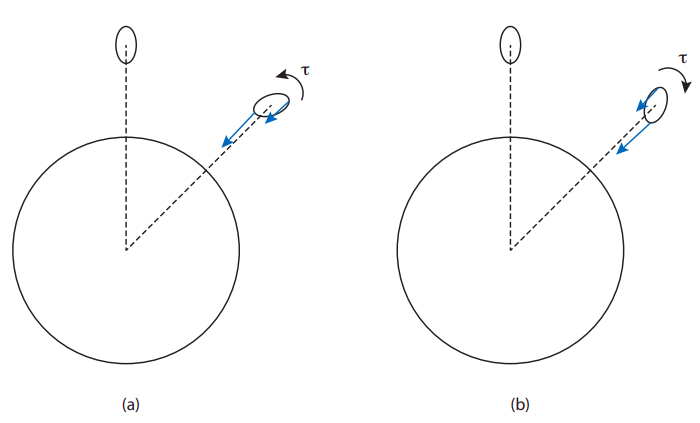
Tenga en cuenta que, por el mismo argumento, esperaríamos que las fuerzas mareales en la Tierra debido a la luna intentaran llevar a la Tierra a un bloqueo de mareas con la luna, es decir, tratar de acercar la duración de un día terrestre a la de un mes lunar. De hecho, las fuerzas de marea de la luna han estado ralentizando la rotación de la Tierra durante miles de millones de años, y continúan haciéndolo en unos 15 microsegundos cada año. Este proceso requiere la disipación de energía, (que de hecho está asociada con las mareas oceánicas: piense en las fuerzas de fricción causadas por las olas, a medida que la marea entra y sale); sin embargo, en la medida en que el sistema Tierra-Luna pueda ser tratado como aislado, su momento angular total no puede cambiar, y así el la ralentización de la Tierra va acompañada de un incremento muy gradual en el radio de la órbita de la luna —aproximadamente 3.8 cm por año, actualmente— para mantener constante el momento angular total.

---

⁵ Quizás preguntes, además de estar estirada, ¿no debería el tirón neto de la luna hacer que la Tierra caiga hacia ella? La respuesta es que la Tierra no cae recta hacia la luna, por la misma razón la luna no cae recta hacia la Tierra: ambas tienen una velocidad lateral que los mantiene en una órbita estable, para lo cual la atracción gravitacional neta proporciona la fuerza centrípeta. Ambos en realidad orbitan alrededor del centro de masa del sistema, que se encuentra a unos 1,690 km bajo la superficie de la Tierra; la órbita de la Tierra (y su velocidad orbital) es mucho menor que la de la luna, en virtud de su masa mucho mayor, por supuesto.