10.1: Momentum

Momentum de una partícula puntual

Podemos definir el momento,\(\vec p\), de una partícula de masa\(m\) y velocidad\(\vec v\) como la cantidad vectorial:

\[\vec p = m\vec v\]

Dado que se trata de una ecuación vectorial, corresponde a tres ecuaciones, una para cada componente del vector de impulso. Cabe señalar que el valor numérico para el momento de una partícula es arbitrario, ya que depende en qué marco de referencia se defina la velocidad de la partícula. Por ejemplo, su velocidad con respecto a la superficie de la Tierra es cero, por lo que su impulso relativo a la superficie de la Tierra es cero. Sin embargo, en relación con la superficie del Sol, tu velocidad, y tu impulso, no son cero. Como veremos, las fuerzas están relacionadas con un cambio de impulso, así como están relacionadas con un cambio en la velocidad (aceleración).

Si la partícula tiene una masa constante, entonces la derivada de tiempo de su impulso viene dada por:

\[\begin{aligned} \frac{d}{dt}\vec p = \frac{d}{dt}m\vec v = m\frac{d}{dt}\vec v=m\vec a\end{aligned}\]

y podemos escribir esto como Segunda Ley de Newton, ya que\(m\vec a\) debe ser igual a la suma vectorial de las fuerzas sobre la partícula de masa\(m\):

\[\frac{d}{dt}\vec p =\sum\vec F=\vec F^{net}\]

La ecuación anterior es la forma original en la que Newton desarrolló por primera vez su teoría. Dice que la fuerza neta sobre un objeto es igual a la tasa de cambio de su impulso. Si la fuerza neta sobre el objeto es cero, entonces su impulso es constante (al igual que su velocidad). En cuanto a componentes, la Segunda Ley de Newton escrita para la tasa de cambio de impulso viene dada por:\[\begin{aligned} \frac{dp_x}{dt} =& \sum F_x\\ \frac{dp_y}{dt} =& \sum F_y\\ \frac{dp_z}{dt} =& \sum F_z\end{aligned}\]

Ejemplo\(\PageIndex{1}\)

Una partícula de masa\(m\) se libera del reposo y se deja caer libremente bajo la influencia de la gravedad cerca de la superficie de la Tierra (supongamos que el arrastre es insignificante). ¿Se conserva la energía mecánica de la partícula? ¿Se conserva el impulso de la partícula? Si no se conserva el impulso, ¿cómo cambia el impulso con el tiempo? ¿Cambian tus respuestas si no se puede ignorar la fuerza del arrastre?

Solución:

Primero, modelamos la partícula que cae asumiendo que no hay fuerza de arrastre. La única fuerza ejercida sobre la partícula es así su peso.

La energía mecánica de la partícula se conservará solo si no hay fuerzas no conservadoras que trabajen sobre la partícula. Dado que la fuerza de gravedad es la única fuerza que actúa sobre la partícula, se conserva su energía mecánica.

El momento total de la partícula no se conserva, porque la suma de las fuerzas sobre la partícula no es cero. Escogiendo el\(z\) eje para que sea vertical y positivo hacia arriba, la Segunda Ley de Newton en la\(z\) dirección viene dada por:

\[\begin{aligned} \sum F_z = -mg=\frac{dp_z}{dt}\end{aligned}\]

Obsérvese que los\(y\) componentes\(x\) y del momento se conservan, ya que no hay fuerzas con componentes en esa dirección. Podemos encontrar cómo el\(z\) componente del impulso cambia con el tiempo tomando el anti-derivado de la fuerza con respecto al tiempo (de\(t=0\) a\(t=T\)):

\[\begin{aligned} \frac{dp_z}{dt} &= -mg\\ \int dp_z &= \int_0^T (-mg) dt\\ p_z(T) - p_z(0) &= -mgT\\ \therefore p_z(T) &= p_z(0) - mgT\end{aligned}\]

donde el\(z\) componente de impulso,\(p_z(T)\) en algún momento\(T\), viene dado por su valor en el tiempo\(t=0\) más\(-mgT\). Si el objeto comenzó en reposo (\(\vec v=0\)), entonces la magnitud del impulso, en función del tiempo, viene dada por:\[\begin{aligned} p(t) = p_z(t) = -mgt\end{aligned}\] y de hecho cambia con el tiempo.

Si la fuerza de arrastre no fuera despreciable, habría una fuerza no conservadora actuando sobre la partícula, por lo que su energía mecánica ya no se conservaría. La partícula se acelerará hasta alcanzar la velocidad terminal. Durante esa fase de aceleración, la fuerza neta sobre la partícula no es cero (se está acelerando), por lo que su impulso no se conserva. Una vez que la partícula alcanza la velocidad terminal, la fuerza neta sobre la partícula es cero, y su momento se conserva a partir de entonces.

Discusión:

Este sencillo ejemplo destaca el hecho de que la energía mecánica y el impulso se conservan bajo diferentes condiciones. El hecho de que uno esté conservado no significa que el otro esté conservado. También muestra que la Segunda Ley de Newton es una declaración sobre el cambio en el impulso, no el impulso en sí (al igual que es una declaración sobre aceleración, cambio de velocidad, no velocidad).

Impulso

Cuando introdujimos el concepto de energía, comenzamos calculando el “trabajo”\(W\), hecho por una fuerza ejercida sobre un objeto sobre un camino específico entre dos puntos: Luego\[\begin{aligned} W = \int_A^B \vec F \cdot d\vec l\end{aligned}\] introdujimos la energía cinética\(K\),, para ser esa cantidad cuyo cambio es igual al trabajo neto hecho en la partícula\[\begin{aligned} W^{net} = \int_A^B \vec F^{net}\cdot d\vec l = \Delta K\end{aligned}\] donde la fuerza neta,\(\vec F^{net}\), es la suma vectorial de las fuerzas sobre la partícula.

Podemos hacer lo mismo, pero en lugar de integrar la fuerza sobre la distancia, podemos integrarla a lo largo del tiempo. Introducimos así el concepto de “impulso”\(\vec J\), de una fuerza, como esa fuerza integrada desde un tiempo inicial\(t_A\), hasta un tiempo final,\(t_B\):

\[\vec J = \int_{t_{A}}^{t_{B}}\vec F dt\]

donde debe quedar claro que el impulso es una cantidad vectorial (y la ecuación vectorial anterior corresponde así a una integral por componente). Impulso es, en general, definido como una integral porque la fuerza,\(\vec F\), podría cambiar con el tiempo. Si la fuerza es constante en el tiempo (magnitud y dirección), entonces podemos definir el impulso sin usar una integral:\[\begin{aligned} \vec J = \vec F \Delta t\end{aligned}\] dónde\(\Delta t\) está la cantidad de tiempo durante el cual se ejerció la fuerza. Aunque la fuerza nunca sea constante, a veces podemos usar la fórmula anterior para calcular el impulso usando un valor promedio de la fuerza.

Ejercicio\(\PageIndex{1}\)

¿Cuál es la unidad SI para impulso?

1. \(\text{kg}\cdot \text{m/s}^{2}\)
2. \(\text{kg} \cdot \text{s}^{2}\)
3. \(\text{kg} \cdot \text{m/s}\)
4. \(\text{kg} \cdot \text{m/s}^{3}\)

Responder

Ejemplo\(\PageIndex{2}\)

Estimar el impulso que se le da a la cabeza de alguien cuando se le da una bofetada en la cara.

Solución:

Cuando le damos una palmada en la cara a alguien con nuestra mano, nuestra mano ejerce una fuerza sobre su rostro durante el periodo de tiempo\(\Delta t\), sobre el cual nuestra mano está en contacto con su rostro. Durante ese periodo de tiempo, la fuerza en su rostro pasa de ser\(0\), a algún valor desagradablemente alto, y luego de vuelta a cero, por lo que la fuerza no puede considerarse constante.

Estimemos la magnitud promedio de la fuerza de bofetada considerando la desaceleración de nuestra mano bofetada y modelando el movimiento como unidimensional. Supongamos que nuestra mano abofeteada tiene una masa\(m=1\text{kg}\) y que es tiene una velocidad de\(2\text{m/s}\) justo antes de que haga contacto. Además, supongamos que está en contacto con el rostro por un periodo de tiempo\(\Delta t\). Esto nos permite encontrar la aceleración promedio de nuestra mano y así la fuerza promedio que ejerce el rostro sobre nuestra mano para detenerla:\[\begin{aligned} a &= \frac{\Delta v}{\Delta t}\\ \therefore F &= ma = m \frac{\Delta v}{\Delta t}\end{aligned}\] Por la Tercera Ley de Newton, la fuerza que desacelera nuestra mano tiene la misma magnitud que la fuerza que nuestra mano ejerce sobre el rostro, permitiéndonos calcular el impulso dado a la cabeza de la persona:\[\begin{aligned} J &= F\Delta t = \left(m \frac{\Delta v}{\Delta t}\right) \Delta t = m\Delta v\\ &=(1\text{kg})(2\text{m/s})=2\text{kg}\cdot \text{m/s}\end{aligned}\]

Discusión:

Obsérvese que el impulso dado a la cabeza corresponde exactamente al cambio de impulso de la mano (\(\Delta p=m\Delta v\)).

Hasta el momento, calculamos el impulso que viene dado por una sola fuerza. También podemos considerar el impulso neto dado a un objeto por la fuerza neta ejercida sobre el objeto:\[\begin{aligned} \vec J^{net} = \int_{t_A}^{t_B}\vec F^{net} dt\end{aligned}\] Compárelo con la Segunda Ley de Newton escrita usando el impulso:\[\begin{aligned} \frac{d}{dt}\vec p &= \vec F^{net}\\ \int_{\vec p_A}^{\vec p_B} d\vec p &= \int_{t_A}^{t_B}\vec F^{net} dt\\ \vec p_B - \vec p_A &= \int_{t_A}^{t_B}\vec F^{net}dt\\ \therefore \Delta \vec p &= \int_{t_A}^{t_B}\vec F^{net} dt\end{aligned}\] y encontramos que el impulso neto recibido por una partícula es precisamente igual a su cambio de impulso:

\[\Delta\vec p = \vec J^{net}\]

Esto es similar a la afirmación de que el trabajo neto realizado sobre un objeto corresponde a su cambio en la energía cinética, aunque hay que tener en cuenta que el impulso es una cantidad vectorial, a diferencia de la energía cinética.

Ejemplo\(\PageIndex{3}\)

Un automóvil que se mueve con una velocidad de\(100\text{km/h}\) collides with a building and comes to a complete stop. The driver and passenger each have a mass of \(80\text{kg}\). The driver wore a seat belt that extended during the collision, so that the force exerted by the seatbelt on the driver acted for about \(2.5\text{s}\). The passenger did not wear a seat belt and instead was slowed down by the force exerted by the dashboard, over a much smaller amount of time, \(0.2\text{s}\). Compare the average decelerating force experienced by the driver and the passenger.

Solución:

Podemos calcular el cambio de impulso de ambas personas, que será igual al impulso que recibieron al chocar con el cinturón de seguridad o con el salpicadero. Ya que conocemos la duración en el tiempo que se ejercieron las fuerzas, podemos calcular la fuerza promedio involucrada para dar el impulso requerido. Podemos suponer que todo esto sucede en una dimensión, así que usamos cantidades escalares en lugar de vectores.

El cambio de impulso a lo largo de la dirección de movimiento, ya sea para el conductor o el pasajero, viene dado por:\[\begin{aligned} \Delta p = p_B - p_A = (0)-p_A=-mv_A\end{aligned}\] dónde\(v_A\) está la velocidad inicial del automóvil, y el impulso final de cualquiera de las personas es cero.

El cambio de impulso es igual al impulso recibido por cualquiera de las personas durante un periodo de tiempo\(\Delta t\), el cual está relacionado con la fuerza que se ejerció sobre ellos:\[\begin{aligned} J=F\Delta t &= \Delta p = -mv_A\\ F&=-m \frac{v_A}{\Delta t}\end{aligned}\] Para el conductor, esto corresponde:\[\begin{aligned} F=(80\text{kg})\frac{(27.8\text{m/s})}{(2.5\text{s})}=890\text{N}\end{aligned}\] y para el pasajero:\[\begin{aligned} F=(80\text{kg})\frac{(27.8\text{m/s})}{(0.2\text{s})}=11120\text{N}\end{aligned}\] La fuerza sobre el conductor es así comparable a su peso, mientras que el pasajero experimenta una fuerza promedio que es más de 10 veces su peso.

Discusión:

Cualquier mecanismo que resulte en un tiempo de colisión más largo ayudará a reducir las fuerzas que están involucradas. Es por ello que los autos están diseñados para arrugarse en colisiones frontales. Esto lo podemos entender en términos del argueo del automóvil absorbiendo parte de la energía cinética del automóvil, además de alargar el tiempo de la colisión para que las fuerzas involucradas sean menores. También es posible que escuches a personas que miran autos modernos que están todos arrugados después de un choque y decir algo como “Seguro que no hacen autos como solían hacerlo”. Pero claro, eso es por diseño; es más seguro si el automóvil se arruga (y los autos están diseñados para arrugarse en áreas específicas, no en la cabina de pasajeros).

Tenga en cuenta que no necesitábamos usar impulso para calcular la fuerza promedio, ya que podríamos haber usado solo la cinemática para determinar la aceleración y la Segunda Ley de Newton para calcular la fuerza correspondiente. Usar impulso es equivalente por construcción, pero a veces, es más fácil matemáticamente.

Sistemas de partículas: fuerzas internas y externas

Hasta ahora, solo hemos utilizado la Segunda Ley de Newton para describir el movimiento de una partícula de masa puntual o para describir el movimiento de un objeto cuya orientación no necesitábamos describir (por ejemplo, un bloque que se desliza por una colina). En esta sección, consideramos lo que sucede cuando hay múltiples partículas puntuales que forman un “sistema”.

En física, definimos vagamente un sistema como el conjunto de objetos/partículas que deseamos describir. Hasta el momento, solo hemos descrito sistemas hechos de una partícula, por lo que describir el movimiento del sistema equivalía a describir el movimiento de esa sola partícula. Un sistema de dos partículas podría ser, por ejemplo, dos bolas de billar sobre una mesa de billar. Para describir ese sistema, necesitaríamos proporcionar funciones que describan las posiciones, velocidades y fuerzas ejercidas sobre ambas bolas. También podemos definir funciones/cantidades que describen el sistema como un todo, en lugar de los detalles. Por ejemplo, podemos definir la energía cinética total del sistema,\(K\), correspondiente a la suma de energías cinéticas de las dos bolas. También podemos definir el impulso total del sistema\(\vec P\), dado por la suma vectorial de los momentos de las dos bolas.

Al considerar un sistema de partículas múltiples, distinguimos entre fuerzas internas y externas. Las fuerzas internas son aquellas fuerzas que las partículas en el sistema ejercen unas sobre otras. Por ejemplo, si las dos bolas de billar del sistema chocan entre sí, cada una ejercerá una fuerza sobre la otra durante la colisión; esas fuerzas son internas. Las fuerzas externas son todas las demás fuerzas ejercidas sobre las partículas del sistema. Por ejemplo, la fuerza de gravedad y la fuerza normal de la mesa de billar son ambas fuerzas externas ejercidas sobre las bolas en el sistema (ejercidas por la Tierra, o por la mesa de billar, ninguna de las cuales consideramos parte del sistema). La fuerza ejercida por una persona que golpea una de las bolas con una cola de alberca es de manera similar una fuerza externa. Lo que consideramos un sistema es arbitrario; podríamos considerar que la mesa de billar y la Tierra forman parte del sistema junto con las dos bolas; en ese caso, la fuerza normal y el peso de las bolas se convertirían en fuerzas internas. La clasificación de si una fuerza es interna o externa a un sistema, por supuesto, depende de lo que se considere parte del sistema.

Ejercicio\(\PageIndex{1}\)

Dos bolas de alberca chocan una contra la otra. ¿Esta fuerza de gravedad ejercida por una bola sobre la otra es una fuerza interna o externa?

1. Interno.
2. Externo.

Responder

La propiedad clave de las fuerzas internas es que la suma vectorial de las fuerzas internas en un sistema es cero. En efecto, la Tercera Ley de Newton establece que por cada fuerza ejercida por\(A\) el objeto sobre el objeto\(B\), hay una fuerza que es igual en magnitud y opuesta en dirección ejercida por\(B\) el objeto sobre el objeto\(A\). Si consideramos que ambos objetos están en un mismo sistema, entonces la suma de las fuerzas internas entre los objetos\(A\) y\(B\) debe sumarse a cero. Es importante señalar que esto es bastante diferente a lo que hemos discutido hasta ahora sobre la suma de fuerzas. Las fuerzas que suman cero se ejercen sobre diferentes objetos. Hasta el momento, solo habíamos considerado sumar fuerzas que se ejercen sobre un mismo objeto para aplicar la Segunda Ley de Newton. Nunca nos hemos encontrado con una situación en la que se sumen fuerzas de “acción” y “reacción”, porque actúan sobre diferentes objetos.

Pensamientos de emma

Fuerzas internas vs. externas - ¿qué es el “sistema” y qué fuerzas debemos considerar?

Como se discutió anteriormente, las fuerzas internas y externas solo pueden considerarse en el contexto de un sistema específico. Entonces, ¿cómo definimos este “sistema”? ¿Hasta dónde llegamos a la hora de definir el sistema?

Por ejemplo, digamos que pateas una pelota de fútbol, y golpea una silla de jardín cercana, derribándola. Se quiere determinar qué pasará con el balón de fútbol después de que golpee la silla de jardín. ¿Qué se define como el sistema aquí y cómo deben clasificarse las fuerzas? ¿Es la fuerza que ejerce el balón de fútbol sobre la silla de jardín una fuerza externa? ¿Debemos considerar la fricción entre la partícula del primer pie que toca la primera partícula de balón de fútbol?

La mejor manera de abordar “definir el sistema” es precisar exactamente lo que estás tratando de modelar. Aquí, específicamente, estás tratando de determinar la velocidad de la pelota después de que golpee la silla de jardín. Ante esta situación, pensar en la fricción entre el pie individual y las partículas del balón de fútbol no nos ayudaría a averiguar la velocidad final del balón de fútbol. Más bien, sería útil pensar en el balón de fútbol y la silla de jardín como dos partículas gigantes y continuas, colisionando e intercambiando energía. Ante esta situación, sería útil considerar el “sistema” como el balón de fútbol y la silla de jardín únicamente.

La fuerza ejercida por el balón de fútbol sobre la silla de jardín sería una fuerza interna, ya que esto nos da información sobre la velocidad final del balón de fútbol y es una fuerza intercambiada entre las partículas dentro del sistema. La fuerza que ejerce la gravedad sobre la silla de jardín, la fuerza normal sobre el pie de la persona y la fuerza ejercida por el pie sobre el balón de fútbol son todas fuerzas que consideraríamos “externas”.

Recuerde: “interna” y “externa” no son propiedades mágicas de un tipo específico de fuerza. Estas definiciones las hacemos nosotros en la búsqueda de construir modelos útiles.

Conservación del impulso

Considerar un sistema de dos partículas con momenta\(\vec p_1\) y\(\vec p_2\). La Segunda Ley de Newton debe sostenerse para cada partícula:\[\begin{aligned} \frac{d\vec p_1}{dt}&=\sum_k \vec F_{1k}\\ \frac{d\vec p_2}{dt}&=\sum_k \vec F_{2k}\end{aligned}\] donde\(F_{ik}\) está la\(k\) -ésima fuerza que está actuando sobre la partícula\(i\). Podemos sumar estas dos ecuaciones juntas:\[\begin{aligned} \frac{d\vec p_1}{dt}+\frac{d\vec p_2}{dt} &= \sum_k \vec F_{1k} + \sum_k \vec F_{2k}\end{aligned}\] La cantidad a la derecha es la suma de las fuerzas ejercidas sobre la partícula 1 más la suma de las fuerzas ejercidas sobre la partícula 2. En otras palabras, es la suma de todas las fuerzas ejercidas sobre todas las partículas del sistema, que podemos escribir como una sola suma. En el lado izquierdo, tenemos la suma de las dos derivadas de tiempo del momenta, que es igual a la derivada temporal de la suma de los momentos. Así podemos reescribir la ecuación como:\[\begin{aligned} \frac{d}{dt}(\vec p_1 + \vec p_2) = \sum \vec F\end{aligned}\] donde, de nuevo, la suma de la derecha es la suma sobre todas las fuerzas ejercidas sobre el sistema. Algunas de esas fuerzas son externas (por ejemplo, la gravedad ejercida por la Tierra sobre las partículas), mientras que algunas de las fuerzas son internas (por ejemplo, una fuerza de contacto entre las dos partículas). Podemos separar la suma en una suma sobre todas las fuerzas externas (\(\vec F^{ext}\)) y una suma sobre las fuerzas internas (\(\vec F^{int}\)):\[\begin{aligned} \sum \vec F = \sum \vec F^{ext} + \sum \vec F^{int} \end{aligned}\] La suma de las fuerzas internas es cero:\[\begin{aligned} \sum \vec F^{int} = 0\end{aligned}\] porque por cada fuerza que ejerce la partícula 1 sobre la partícula 2, habrá una igual y opuesta fuerza ejercida por la partícula 2 sobre la partícula 1. Tenemos así:\[\begin{aligned} \frac{d}{dt}(\vec p_1 + \vec p_2) = \sum \vec F^{ext}\end{aligned}\] Además, si introducimos el “impulso total del sistema”\(\vec P=\vec p_1 + \vec p_2\), como la suma de los momentos de las partículas individuales, encontramos:\[\begin{aligned} \frac{d\vec P}{dt} &= \sum \vec F^{ext}\end{aligned}\] que es el equivalente de la Segunda Ley de Newton para un sistema donde,\(\vec P\), es el impulso total de el sistema, y la suma de las fuerzas es sólo por encima de las fuerzas externas al sistema.

Tenga en cuenta que la derivación anterior se extiende fácilmente a cualquier número\(N\),, de partículas, aunque solo lo hicimos con\(N=2\). En general, para la “iésima partícula”, con ímpetu\(\vec p_i\), podemos escribir la Segunda Ley de Newton:\[\begin{aligned} \frac{d\vec p_i}{dt}=\sum_k \vec F_{ik}\end{aligned}\] donde la suma supera solo aquellas fuerzas ejercidas sobre la partícula\(i\). Sumando la ecuación anterior para todas\(N\) las partículas del sistema:\[\begin{aligned} \frac{d}{dt}\sum_i \vec p_i=\sum \vec F^{ext} + \sum \vec F^{int}\end{aligned}\] donde la suma sobre las fuerzas internas desaparecerá por la misma razón que la anterior. Introduciendo el impulso total del sistema,\(\vec P\):\[\begin{aligned} \vec P = \sum_i \vec p_i\\\end{aligned}\] Podemos escribir una ecuación para la derivada del tiempo del impulso total del sistema:

\[\frac{d\vec P}{dt}=\sum\vec F^{ext}\]

donde la suma de las fuerzas es la suma sobre todas las fuerzas externas al sistema. Así, si no hay fuerzas externas en un sistema, entonces se conserva el impulso total de ese sistema (si la derivada en el tiempo de una cantidad es cero entonces esa cantidad es constante).

Ya argumentamos en el apartado anterior que podemos hacer internas todas las fuerzas si elegimos que nuestro sistema sea lo suficientemente grande. Si hacemos que el sistema sea el Universo, entonces no hay fuerzas externas al Universo, y el impulso total del Universo debe ser constante:\[\begin{aligned} \frac{d\vec P^{Universe}}{dt} &= \sum_{Universe} \vec F^{ext} = 0 \\ \therefore \vec P^{Universe}&=\text{constant}\end{aligned}\]

En resumen, vimos que:

• Si no se ejercen fuerzas sobre una sola partícula, entonces el impulso de esa partícula es constante (conservado).
• En un sistema de partículas, el momento total del sistema se conserva si no hay fuerzas externas sobre el sistema.
• Si no hay fuerzas no conservadoras ejercidas sobre una partícula, entonces la energía mecánica de esa partícula es constante (conservada).
• En un sistema de múltiples partículas, la energía mecánica total del sistema se conservará si no hay fuerzas no conservadoras ejercidas sobre el sistema.

Cuando nos referimos a una fuerza que es “ejercida sobre un sistema”, nos referimos a ejercida sobre una o más de las partículas del sistema. En particular, la suma del trabajo realizado por las fuerzas internas no es necesariamente cero, por lo que la energía y el impulso se conservan en diferentes condiciones.

Ejemplo\(\PageIndex{4}\)

Figura\(\PageIndex{1}\): Un tren con\(N\) vagones de masa a\(m\) punto de chocar con un carro de masa\(m\) que se encuentra en reposo en la vía.

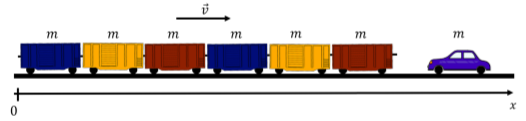
Considera un tren hecho de\(N\) cars of equal mass \(m\) that is traveling at constant speed \(v\) along a straight piece of track where friction and drag are negligible, as depicted in Figure \(\PageIndex{1}\). An empty car of mass \(m\) was left at rest on the track in front of the train. The train collides with the empty car which stays attached to the front of the train. What is the speed of the train after the collision? Is the total mechanical energy of the system conserved?

Solución:

Cuando el tren choca con el carro, ejercerá una fuerza de “colisión” sobre el carro, y el carro ejercerá una fuerza opuesta sobre el tren. Si consideramos que tanto el tren como el automóvil forman parte del mismo sistema, entonces esas fuerzas de colisión serán internas, y se conservará el impulso del sistema (tren + carro). Tanto el tren como el automóvil experimentan fuerzas externas de la gravedad de la Tierra y la fuerza normal de las vías del tren. Sin embargo, esos dos conjuntos de fuerzas se anulan entre sí, ya que ni el tren ni el carro tienen ninguna aceleración en la dirección vertical (la suma de las fuerzas sobre cada objeto no tiene componente vertical neto). Por lo tanto, no hay fuerzas externas netas en el sistema coche+tren, y el impulso total del sistema se conserva a través de la colisión.

Podemos modelar este sistema en una dimensión (a lo largo de la vía), definiendo nuestro\(x\) eje. Elegimos el suelo como marco de referencia, la dirección positiva paralela a la velocidad inicial del tren, y el origen a ubicar donde arranca inicialmente el carro. Antes de la colisión, el\(x\) componente de los momentos del tren (masa\(Nm\)) y carro (masa\(m\)) son:\[\begin{aligned} p_{train}&=Nmv\\ p_{car}&=0\end{aligned}\] Después de la colisión, el carro se une al tren (y así tiene la misma velocidad,\(v'\)), por lo que el momento del tren y auto después de la colisión son:\[\begin{aligned} p'_{train}&=Nmv'\\ p'_{car}&=mv'\end{aligned}\] donde los primos\('\) denotan cantidades después de la colisión. Aplicando la conservación del impulso al sistema, el impulso total antes y después de la colisión debe ser igual:\[\begin{aligned} p_{train}+p_{car}&=p'_{train}+p'_{car}\\ \therefore Nmv &= Nmv' +mv'\\ \therefore v' &=\frac{N}{N+1}v\end{aligned}\] y la velocidad del tren con el carro adicional adjunto se reduce en un factor\(N/(N+1)\) en comparación con lo que era antes de la colisión.

Podemos verificar para ver si se conserva la energía mecánica del sistema, ya que conocemos las velocidades del tren y del carro antes y después de la colisión. Dado que todo el movimiento es horizontal, la gravedad y la fuerza normal no funcionan ni en el tren ni en el automóvil, por lo que su energía mecánica puede ser tomada como su energía cinética (su energía potencial gravitacional no cambia después de la colisión). La energía mecánica total del sistema,\(E\), antes de la colisión es la energía cinética del tren:\[\begin{aligned} E= \frac{1}{2}Nmv^2\end{aligned}\] La energía mecánica total del sistema,\(E'\), después de la colisión es:\[\begin{aligned} E' &= \frac{1}{2}Nmv'^2 + \frac{1}{2}mv'^2 = \frac{1}{2}(N+1)mv'^2 \\ &=\frac{1}{2}(N+1)m \left( \frac{N}{N+1}v \right)^2\\ &=\frac{1}{2}m\frac{N^2}{N+1}v^2\end{aligned}\] y vemos eso\(E'<E\), y así que el total la energía mecánica del sistema no se conserva (se reduce después de la colisión).

Discusión:

Podríamos haber resuelto este problema modelando cuidadosamente la fuerza ejercida por el carro sobre el tren durante la colisión, lo que nos hubiera permitido encontrar la velocidad del tren después de la colisión utilizando su aceleración. Esto habría requerido un modelo detallado para esa fuerza, que no tenemos. Sin embargo, al darnos cuenta de que el tren y el automóvil podrían considerarse como un sistema sin que se ejerzan fuerzas externas netas sobre él, pudimos encontrar fácilmente la velocidad del tren después de la colisión utilizando la conservación del impulso.

También se encontró que la energía mecánica no se conservaba. Esto tiene sentido físico porque, para que el carro permaneciera apegado al tren, presumiblemente tuvieron que haber algunas fuerzas significativas en juego que “aplastaron” al carro en el tren. Parte de la energía cinética inicial del tren se utilizó para deformar el tren y el automóvil durante la colisión. También podemos pensar en deformar un material como darle energía. A veces esa energía es recuperable (por ejemplo, comprimir un resorte), a veces, no lo es (por ejemplo, aplastar un automóvil).

Si el carro y el tren estuvieran equipados con resortes grandes para absorber la energía del impacto, la colisión podría haber conservado energía mecánica, ya que los resortes se comprimen y luego se expanden hacia atrás. La velocidad del carro y del tren sería entonces diferente después de la colisión en este caso (ver Ejemplo 10.2.3). Es una característica de las colisiones donde los dos cuerpos permanecen unidos entre sí que la energía mecánica no se conserva.