12.6: Problemas y soluciones de la muestra

Ejercicio\(\PageIndex{1}\)

Un yoyo se puede modelar como dos discos uniformes, de radio\(R_{2}\), unidos a cada lado de un disco uniforme más pequeño de radio\(R_{1}\), como en la Figura\(\PageIndex{1}\). Podemos suponer que los tres discos tienen una masa\(m\). Una cuerda sin masa se envuelve alrededor del disco más pequeño y luego se libera el yoyo. ¿Cuál es la aceleración del centro de masa del yoyo a medida que cae y la cuerda se desenrolla?

Figura\(\PageIndex{1}\): Izquierda: Vista lateral del yoyo. Derecha: Vista frontal del yoyo, modelada como dos discos de radio de\(R_{2}\) unidos a cada lado de un disco de radio\(R_{1}\).

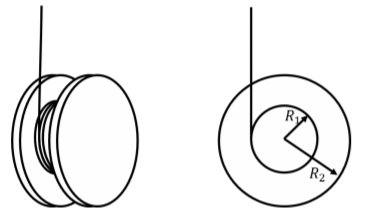
Responder

Las fuerzas que actúan sobre el yoyo son

• \(\vec F_{g}\), su peso, con magnitud\(3mg\).
• \(\vec T\), una fuerza de tensión de la cuerda

Las fuerzas, donde se ejercen, y nuestra elección del sistema de coordenadas se muestran en la Figura\(\PageIndex{2}\).

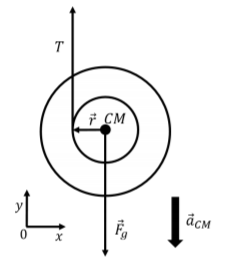
Figura\(\PageIndex{2}\): Diagrama de cuerpo libre para el yoyo.

El yoyo se puede modelar como rodando sin resbalar, como si estuviera rodando a lo largo de la cuerda que se desenrolla. El par alrededor del centro de masa es proporcionado por la tensión en la cuerda. La aceleración angular del yoyo,\(α\), estará relacionada con la aceleración lineal del centro de masa\(\vec a_{CM}\), ya que ésta es rodando sin deslizarse:

\[\begin{aligned} a_{CM}=\alpha R_{1} \end{aligned}\]

donde\(R_{1}\) es el radio que es análogo al movimiento rodante. Dado que el par de torsión de la fuerza de gravedad es cero, podemos escribir la Segunda Ley de Newton para cantidades rotacionales como:

\[\begin{aligned} \vec\tau ^{ext}&=I\vec\alpha \\ TR_{1}=I\alpha \end{aligned}\]

donde\(TR_{1}\) está la magnitud del par de torsión a partir de la fuerza de tensión, ya que la tensión es perpendicular al vector\(\vec r\) entre el centro de masa y el punto donde se ejerce la tensión. El momento de inercia del yoyo alrededor de su centro de masa es la suma de los momentos de inercia de los tres discos alrededor de su eje de simetría:

\[\begin{aligned} I = \frac{1}{2}MR_{2}^{2} +\frac{1}{2}MR_{2}^{2} +\frac{1}{2}MR_{1}^{2} =\frac{1}{2}M(2R_{2}^{2}+R_{1}^{2} \end{aligned}\]

También podemos escribir la Segunda Ley de Newton en dirección vertical para el yoyo (de masa\(3M\)):

\[\begin{aligned} \sum F_{y} &=-F_{g}+T=-3Ma_{CM} \\ -3MG +T &=-3Ma_{CM} \end{aligned}\]

donde estamos\(a_{CM}\) la magnitud de la aceleración del centro de masa (ya que incluimos el signo en la primera ecuación).

Podemos eliminar la fuerza desconocida de tensión de las ecuaciones por sustitución. Usando la ecuación de la Segunda Ley de Newton:

\[\begin{aligned} T=3M(g-a_{CM}) \end{aligned}\]

y sustituyendo esto en la ecuación rotacional:

\[\begin{aligned} TR_{1}&=I\alpha \\ 3M(g-a_{CM})R_{1}&=I\alpha \end{aligned}\]

Podemos resolver\(a_{CM}\) por el uso de la condición para rodar sin resbalar\((αR_{1} = a_{CM})\):

\[\begin{aligned} 3M(g-a_{CM})R_{1}&=I\frac{a_{CM}}{R_{1}} \\ \frac{I}{R_{1}}a_{CM}+3MR_{1}a_{CM} &=3MgR_{1} \\ a_{CM}\left( \frac{I}{R_{1}}+3MR_{1} \right) &=3MgR_{1} \\ a_{CM}&=\frac{3MgR_{1}}{\frac{I}{R_{1}}+3MR_{1}} \\ &=\frac{3MgR_{1}}{\frac{\frac{1}{2} M(2R_{2}^{2}+R_{1}^{2})}{R_{1}} + 3MR_{1}} \\ &= \left(\frac{3R_{1}^{2}}{\frac{1}{2}(2R_{2}^{2}+R_{1}^{2})+3R_{1}^{2}} \right) g \\ \therefore a_{CM} &= \left(\frac{3R_{1}^{2}}{R_{2}^{2}+\frac{7}{2}R_{1}^{2}} \right) g \end{aligned}\]

Ejercicio\(\PageIndex{2}\)

Figura\(\PageIndex{3}\): Un proyectil de masa\(m\) está a punto de chocar con un disco que puede girar alrededor de su eje de simetría. Vista desde arriba.

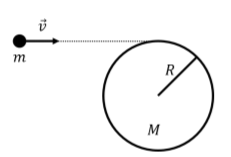
\(m\)Se dispara un proyectil de masa hacia un disco estacionario de radio\(R\) y masa\(M\) que se encuentra sobre una mesa horizontal, como se representa desde arriba en la Figura\(\PageIndex{3}\). El disco está en el plano horizontal y puede girar alrededor de un eje vertical a través de su centro. El eje alrededor del cual gira el disco está unido a la mesa y no puede moverse. La velocidad del proyectil,\(\vec v\), es horizontal y tal que el proyectil se incrusta en el borde del disco. ¿Cuál es la velocidad angular del disco, sobre su centro, después de que el proyectil se haya incrustado en el disco? ¿La colisión fue elástica? ¿Se conservó el impulso lineal durante la colisión?

Responder

Consideramos el proyectil y el disco como un sistema, y un eje de rotación que pasa por el centro del disco. No hay pares externos ejercidos sobre el sistema alrededor del eje de rotación, por lo que el momento angular del sistema debe conservarse a través de la colisión. Antes de la colisión, solo el proyectil tiene un momento angular alrededor del eje de rotación, por lo que la magnitud del momento angular antes de la colisión es:

\[\begin{aligned} L=rp\sin\phi \end{aligned}\]

donde\(φ\) es el ángulo entre el momento de la partícula\(\vec p = m\vec v\), y un vector,\(\vec r\), desde el eje de rotación a la partícula. Podemos calcular el momento angular de la partícula justo antes de la colisión, de manera que ese\(\vec r\) es el vector desde el centro del círculo hasta el punto donde la partícula colisiona (con magnitud\(R\), y perpendicular a\(\vec v\)). El momento angular inicial del sistema es así:

\[\begin{aligned} L=rp=Rmv \end{aligned}\]

Después de la colisión, el proyectil queda incrustado en el disco. El objeto resultante tiene un momento de inercia dado por:

\[\begin{aligned} I = I_{disk}+I_{particle}=\frac{1}{2}MR^{2}+mR^{2} \end{aligned}\]

Después de la colisión, el momento angular del disco con el proyectil incrustado viene dado por:

\[\begin{aligned} L' = I\omega = \left(\frac{1}{2}M+m \right) R^{2}\omega \end{aligned}\]

Usando la conservación del momento angular, la velocidad angular del disco después de la colisión es:

\[\begin{aligned} L&=L' \\ Rmv&=\left(\frac{1}{2}M+m \right)R^{2}\omega \\ \therefore\omega &=\frac{mv}{\left(\frac{1}{2}M+m \right)R} \end{aligned}\]

No esperamos que la energía mecánica se conserve durante la colisión, ya que el proyectil se incrusta a sí mismo, lo que debe costar energía. La energía mecánica antes de la colisión viene dada por la energía cinética del proyectil:

\[\begin{aligned} E=\frac{1}{2}mv^{2} \end{aligned}\]

Después de la colisión, la energía cinética es la energía cinética rotacional del disco con proyectil incrustado alrededor del eje de rotación:

\[\begin{aligned} E'&=\frac{1}{2}I\omega ^{2}=\frac{1}{2}\left(\frac{1}{2}M+m \right) R^{2}\left( \frac{mv}{(\frac{1}{2}M+m)R} \right)^{2} \\ &=\frac{1}{2} \frac{m^{2}}{(\frac{1}{2}M+m)}v^{2} \end{aligned}\]

Podemos ver que\(E'\) es menor que\(E\), tomando su ratio:

\[\begin{aligned} \frac{E'}{E}&=\frac{\frac{1}{2}\frac{m^{2}}{(\frac{1}{2}M+m)}v^{2}}{\frac{1}{2}mv^{2}} \\ &=\frac{m}{(\frac{1}{2}M+m)}<1 \end{aligned}\]

y confirmamos que la energía mecánica no se conserva en la colisión (y esa energía se perdió ya que se tuvo que deformar el proyectil y el disco).

El momento lineal claramente no se conserva ya que el momento lineal final es cero, mientras que antes de la colisión, lo es\(\vec p = m\vec v\). El centro de masa del sistema disco+proyectil se mueve antes de la colisión y no después. Por lo tanto, debe haber una fuerza externa neta que se ejerza sobre el sistema. Esa fuerza es ejercida por la mesa sobre el eje del disco, ya que el disco de otra manera retraería al ser golpeado con el proyectil.

Discusión:

En este ejemplo, se utilizó la conservación del momento angular para modelar una colisión. El choque es inelástico, porque el proyectil se incrusta en el disco. El momento lineal no se conserva a través de la colisión debido a que el eje alrededor del cual gira el disco debe ejercer una fuerza sobre el disco para evitar que se deslice.