14.1: Características de una ola

Definición y tipos de ondas

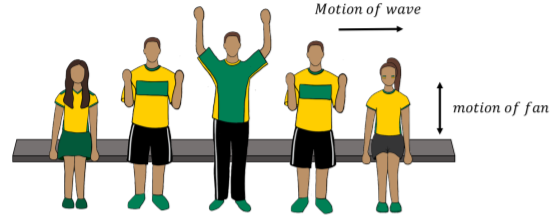
Una onda viajera es una perturbación que viaja a través de un medio. Considera las olas que hicieron los aficionados en un partido de futbol, como en la Figura\(\PageIndex{1}\). Se puede pensar en los abanicos como el medio a través del cual se propaga la ola. Los elementos del medio pueden oscilar alrededor de una posición de equilibrio (los ventiladores se mueven una corta distancia hacia arriba y hacia abajo), pero no viajan con la ola (los ventiladores no se mueven horizontalmente con la ola).

Figura\(\PageIndex{1}\): Una ola transversal hecha por aficionados al fútbol moviéndose hacia arriba y hacia abajo.

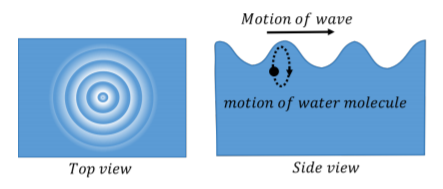
Considera las ondas (olas) hechas por una roca caída en un estanque (Figura\(\PageIndex{2}\)). Las ondas viajan hacia afuera desde donde se dejó caer la roca, pero el agua en sí no se mueve hacia afuera. Las moléculas de agua individuales se moverán en pequeños círculos alrededor de una posición de equilibrio, pero no se mueven junto con las olas.

Figura\(\PageIndex{2}\): Onda transversal que viaja a través del agua. El panel izquierdo muestra la vista desde arriba a medida que las ondas se mueven hacia afuera. El panel derecho muestra el movimiento de una molécula de agua individual a medida que la ola se ve desde un lado.

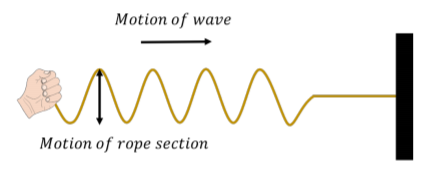
Podemos distinguir entre dos clases de ondas, con base en el movimiento del medio a través del cual se propaga. Con las ondas transversales, los elementos del medio oscilan de un lado a otro en una dirección perpendicular al movimiento de la ola. Por ejemplo, si une una cuerda horizontal a una pared y mueve el otro extremo hacia arriba y hacia abajo (Figura\(\PageIndex{3}\)), puede crear una perturbación (una ola) que se desplaza horizontalmente a lo largo de la cuerda. Las partes de la cuerda no se mueven horizontalmente; solo se mueven hacia arriba y hacia abajo, alrededor de alguna posición de equilibrio.

Figura\(\PageIndex{3}\): Una onda transversal que viaja a través de una cuerda. La ola se crea moviendo un extremo de la cuerda hacia arriba y hacia abajo.

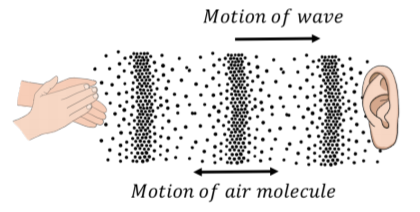
Con las ondas longitudinales, los elementos del medio oscilan hacia adelante y hacia atrás en la misma dirección que el movimiento de la ola. Si aplaudes, crearás una perturbación de presión en el aire que se propagará; esto es lo que llamamos sonido (una onda sonora). Las moléculas de aire oscilan alrededor de una posición de equilibrio en la misma dirección en la que se propaga la onda, pero no se mueven con la ola.

Figura\(\PageIndex{4}\): Una onda de sonido longitudinal que viaja por el aire. Las moléculas de aire se mueven hacia adelante y hacia atrás en la misma dirección que la onda, pero oscilan alrededor de una posición de equilibrio en lugar de moverse con la ola.

Además, podemos distinguir entre “ondas viajeras”, en las que una perturbación se propaga a través de un medio, y “ondas estacionarias”, que no transportan energía a través del medio (por ejemplo, una cuerda vibratoria en un violín).

Ejercicio\(\PageIndex{1}\)

¿Las ondas se propagan a través de un slinky cuando lo comprimes y alargas (Figura\(\PageIndex{5}\)) transversal o longitudinal?

Figura\(\PageIndex{5}\): Una ola que viaja a través de un slinky. La onda se crea cuando comprimes o alargas el slinky

1. Transversal
2. longitudinal

Contestar

Físicamente, una onda solo puede propagarse a través de un medio si el medio puede deformarse. Cuando una partícula en el medio es perturbada desde su posición de equilibrio, experimentará una fuerza restauradora que actúa para devolverla a su posición de equilibrio. A menudo, si el desplazamiento de la partícula del equilibrio es pequeño, la magnitud de esa fuerza es proporcional al desplazamiento. Así, como veremos, podemos modelar la propagación de las ondas tratando las partículas en el medio como simples osciladores armónicos.

Se requiere una fuente de energía para deformar el medio y generar una onda. Por ejemplo, esa fuente de energía podría ser un altavoz que crea ondas sonoras empujando una membrana hacia adelante y hacia atrás; los altavoces requieren energía y, a menudo, son clasificados por la energía eléctrica que convierten en ondas sonoras (por ejemplo, un\(50\text{W}\) altavoz consume\(50\text{W}\) energía eléctrica para producir sonido).

Figura\(\PageIndex{6}\): Un altavoz que crea ondas sonoras sonoras. La membrana vibra de un lado a otro lo que deforma el aire para crear ondas sonoras que se propagan a través del aire.

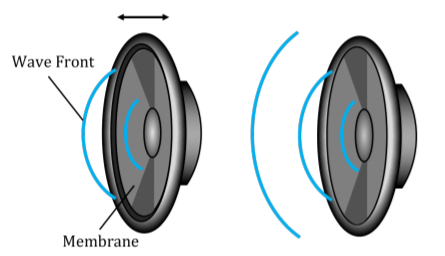
Descripción de una ola

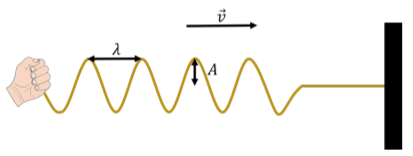
En este capítulo, discutiremos principalmente cómo describir las ondas sinusoidales; aquellas para las cuales el desplazamiento de partículas en el medio puede describirse mediante una función de posición que varía sinusoidalmente. Como veremos, las ondas más complicadas siempre pueden describirse como si fueran la combinación de múltiples ondas sinusoidales. Podemos usar varias cantidades para describir una ola viajera, las cuales se ilustran en la Figura\(\PageIndex{7}\):

• La longitud de onda\(\lambda\),, es la distancia entre dos máximos sucesivos (“picos”) o mínimos (“valles”) en la onda.
• La amplitud,\(A\), es la distancia máxima a la que una partícula en el medio se desplaza de su posición de equilibrio.
• La velocidad,\(\vec v\), es la velocidad con la que la perturbación se propaga a través del medio.
• El periodo,\(T\), es el tiempo que tarda dos máximos (o mínimos) sucesivos en pasar por el mismo punto en el medio.
• La frecuencia,\(f\), es la inversa del periodo (\(f=1/T\)).

Figura\(\PageIndex{7}\): Longitud de onda, velocidad y amplitud para una onda transversal en una cuerda.

La longitud de onda, la velocidad y el periodo de la onda están relacionados, ya que la cantidad de tiempo que tardan dos máximos sucesivos de la onda en pasar por un punto determinado dependerá de la velocidad de la onda y de la distancia entre máximos,\(\lambda\). Dado que lleva un tiempo,\(T\), para que dos máximos\(\lambda\) separados por distancia pasen por un punto dado en el medio, la velocidad de la ola viene dada por:

\[v=\frac{\lambda}{T}=\lambda f\]

Así, de las tres cantidades (velocidad, período/frecuencia y longitud de onda), sólo dos son independientes, ya que la tercera cantidad debe depender del valor de las otras dos. La velocidad de una onda depende de las propiedades del medio a través del cual se propaga la onda y no del mecanismo que está generando la onda. Por ejemplo, la velocidad de las ondas sonoras depende de la presión, densidad y temperatura del aire a través del cual se propagan, y no de lo que está haciendo el sonido. Cuando un mecanismo genera una onda, ese mecanismo suele determinar la frecuencia de la onda (por ejemplo, la frecuencia con la que la mano en la Figura\(\PageIndex{7}\) se mueve hacia arriba y hacia abajo), la velocidad es determinada por el medio, y la longitud de onda puede determinarse a partir de la Ecuación 14.1.1.

Ejercicio\(\PageIndex{2}\)

¿Qué se puede decir del sonido que emite un violonchelo versus el que emite un violín?

1. El sonido del violín tiene una mayor frecuencia.
2. El sonido del violonchelo tiene una longitud de onda más larga.
3. El sonido de ambos instrumentos se propaga a la misma velocidad.
4. Todo lo anterior.

Contestar