2.1: La ecuación de onda unidimensional
- Page ID
- 80187
- Introducir la ecuación de onda incluyendo la dependencia del tiempo y la posición
En el sentido más general, las ondas son partículas u otros medios con propiedades y estructura onduladas (presencia de crestas y depresiones).
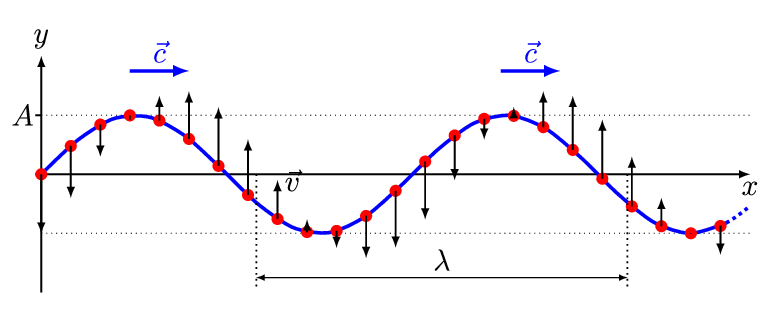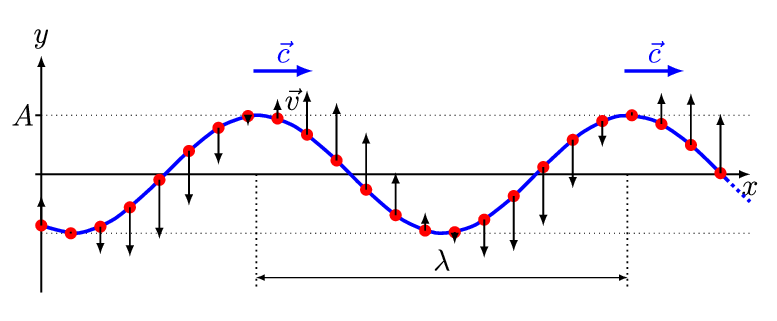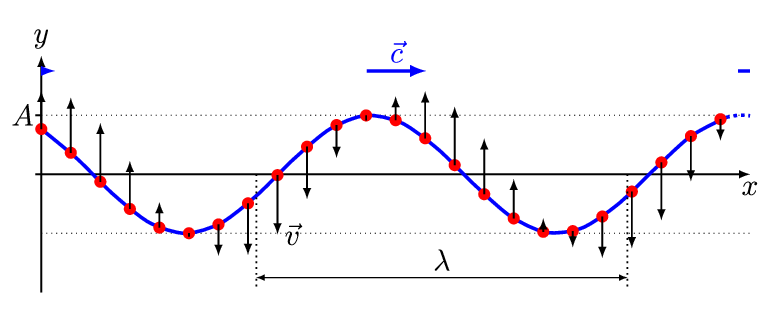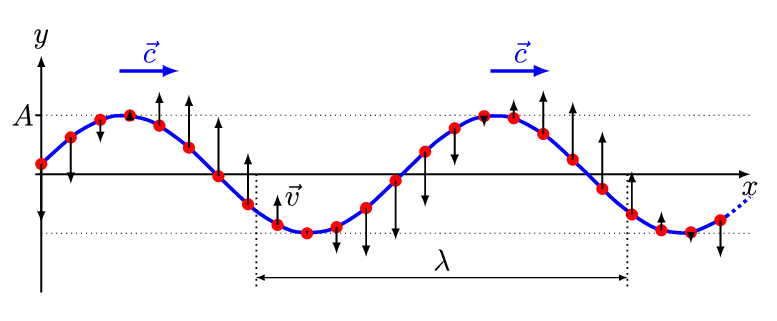
La onda más simple es la onda sinusoidal unidimensional (espacialmente) (Figura 2.1.1 ) con una amplitud variable\(A\) descrita por la ecuación:
\[ A(x,t) = A_o \sin (kx - \omega t + \phi) \nonumber \]
donde
- \(A_o\)es la amplitud máxima de la onda, distancia máxima desde el punto más alto de la perturbación en el medio (la cresta) hasta el punto de equilibrio durante un ciclo de onda. En la Figura 2.1.1 , esta es la distancia vertical máxima entre la línea base y la onda.
- \(x\)es la coordenada del espacio
- \(t\)es la coordenada de tiempo
- \(k\)es el número de onda
- \(\omega\)es la frecuencia angular
- \(\phi\)es la constante de fase.
Se pueden clasificar las “olas” en dos grupos diferentes: ondas viajeras y ondas estacionarias.
Olas Viajeras
Las olas viajeras, como las olas oceánicas o la radiación electromagnética, son ondas que “se mueven”, lo que significa que tienen una frecuencia y se propagan a través del tiempo y el espacio. Otra forma de describir esta propiedad del “movimiento de las olas” es en términos de transmisión de energía: una ola viaja, o transmite energía, sobre una distancia establecida. Los tipos más importantes de ondas viajeras en la vida cotidiana son las ondas electromagnéticas, las ondas sonoras y quizás las ondas de agua, dependiendo de dónde vivas. Es difícil analizar las ondas que se extienden en tres dimensiones, reflejándose en objetos, etc., por lo que comenzamos con los ejemplos más simples e interesantes de olas, los restringidos a moverse a lo largo de una línea. Empecemos con una cuerda, como un tendedero, estirada entre dos ganchos. Sacas un extremo del gancho, sujetando la cuerda, y, manteniéndola estirada bastante apretada, agitas la mano hacia arriba y hacia atrás una vez. Si lo haces lo suficientemente rápido, verás un solo golpe viajar a lo largo de la cuerda:
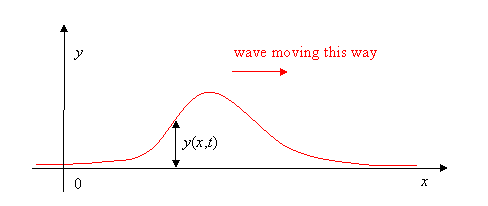
Este es el ejemplo más simple de una ola viajera. Puedes hacer olas de diferentes formas moviendo tu mano hacia arriba y hacia abajo en diferentes patrones, por ejemplo un golpe hacia arriba seguido de una caída, o dos golpes. Encontrarás que la ola viajera mantiene la misma forma a medida que se mueve hacia abajo por la cuerda. Tomando la cuerda para que se estire lo suficiente como para que podamos llevarla a ser horizontal, usaremos su posición de reposo como nuestro eje x (Figura 2.1.1 ). El\(y\) eje -se toma verticalmente hacia arriba, y solo agitamos la cuerda de una manera arriba y abajo, así que en realidad\(y(x,t)\) será lo lejos que está la cuerda de su posición de reposo en el\(x\) momento\(t\): es decir, la Figura 2.1.2 muestra dónde está la cuerda en un solo momento\(t\).
Ahora podemos expresar la observación de que la ola “mantiene la misma forma” con mayor precisión. Tomando por conveniencia tiempo\(t = 0\) para ser el momento en que pasa el pico de la ola\(x = 0\), graficamos aquí la posición de la cuerda en t = 0 y algunos momentos posteriores\(t\) como una película (Figura 2.1.3 ). Denotando la primera función por\(y(x,0) = f(x)\), luego la segunda\(y(x,t) = f(x- v t)\): es la misma función con la “misma forma”, pero simplemente movida por\(v t\), donde\(v\) está la velocidad de la onda.

Para resumir: al enviar una onda viajera por una cuerda sacudiendo el extremo hacia arriba y hacia abajo, a partir de la observación la ola viaja a velocidad constante y mantiene su forma, por lo que el desplazamiento y de la cuerda en cualquier posición horizontal en el\(x\) momento\(t\) tiene la forma
\[y(x,t)=f(x-v t) \label{2.1.0} \]
Estamos descuidando los efectos de fricción: en una cuerda real, la protuberancia gradualmente se hace más pequeña a medida que avanza.
Ondas Standing
A diferencia de las olas viajeras, las ondas estacionarias o estacionarias, permanecen en una posición constante con crestas y canales en intervalos fijos. Una forma de producir una variedad de ondas estacionarias es desplumando una melodía en un juego de cuerdas de guitarra o violín. Al colocar el dedo sobre una parte de la cuerda y luego arrancarla con otra, se ha creado una onda estacionaria. Las soluciones a este problema implican que la cadena oscile en un patrón de onda sinusoidal (Figura 2.1.4 ) sin vibración en los extremos. Tampoco hay vibración en una serie de puntos equidistantes entre los extremos; estos lugares “silenciosos” son nodos. Los lugares de máxima oscilación son los antinodos.
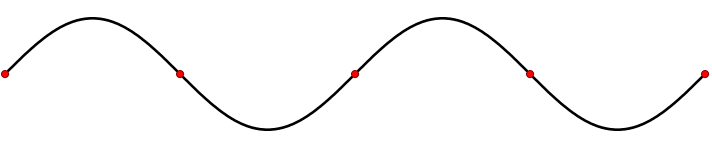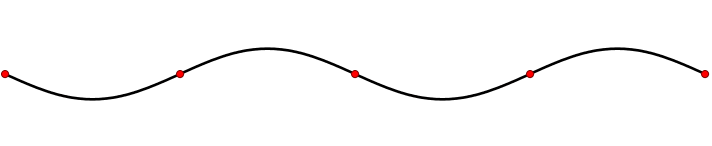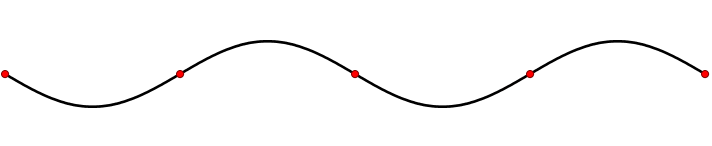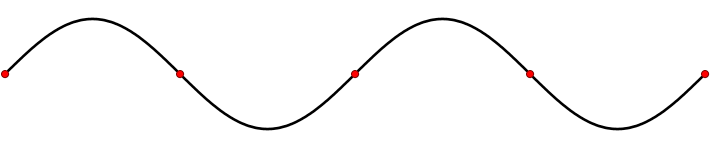
Las ondas viajeras exhiben movimiento y se propagan a través del tiempo y el espacio y las ondas estacionarias tienen crestas y depresiones a intervalos fijos separados por nodos. Las partículas “libres” como el fotoelectrón discutido en el efecto fotoelectrón, exhiben propiedades similares a ondas viajeras. En contraste, los electrones que son ondas “unidas” exhibirán propiedades similares a ondas estacionarias. Este último fue invocado para el átomo de Bohr para cuantificar el momento angular de un electrón unido dentro de un átomo de hidrógeno.
La Ecuación de Onda
La descripción matemática de las ondas unidimensionales (tanto de viaje como de pie) se puede expresar como
\[ \dfrac{\partial^2 u(x,t)}{\partial x^2} = \dfrac{1}{v^2} \dfrac{\partial^2 u(x,t)}{\partial t^2} \label{2.1.1} \]
con\(u\) es la amplitud de la onda en posición\(x\) y tiempo\(t\), y\(v\) es la velocidad de la onda (Figura 2.1.2 ).
La ecuación\(\ref{2.1.1}\) se denomina ecuación de onda clásica en una dimensión y es una ecuación diferencial parcial lineal. Nos dice cómo el desplazamiento\(u\) puede cambiar en función de la posición y el tiempo y la función. Las soluciones a la ecuación de onda (\(u(x,t)\)) se obtienen mediante técnicas de integración apropiadas. Puede que no sea sorprendente que no todas las ondas posibles satisfagan Ecuación\(\ref{2.1.1}\) y las ondas que sí deben satisfacer tanto las condiciones iniciales como las condiciones límite, es decir, sobre cómo se produce la onda y lo que está sucediendo en los extremos de la cuerda.
Por ejemplo, para una onda estacionaria de cuerda con longitud\(L\) tensa en dos extremos (Figura 2.1.3 ), las condiciones de contorno son
\[u(0,t)=0\ \label{2.1.3a} \]
y
\[u(L,t)=0 \label{2.1.3b} \]
para todos los valores de\(t\). Como era de esperar, diferentes sistemas tendrán diferentes condiciones de límite y por lo tanto diferentes soluciones.
Las condiciones iniciales y las condiciones límite utilizadas para resolver la ecuación de onda resultarán en restricciones de ondas “permitidas” para existir de manera similar que solo existen ciertas soluciones para los electrones en el átomo de Bohr.
Las primeras seis soluciones de onda\(u(x,t)\) a la Ecuación\(\ref{2.1.1}\) están sujetas a las condiciones de límite en Ecuaciones\(\ref{2.1.3a}\) y\(\ref{2.1.3b}\) (discutidas en detalle más adelante) dan como resultado la onda en la Figura 2.1.5 . Se trata de ondas estacionarias que existen con frecuencias basadas en el número de nodos (0, 1, 2, 3,...) que exhiben (más discutidos en la siguiente Sección).
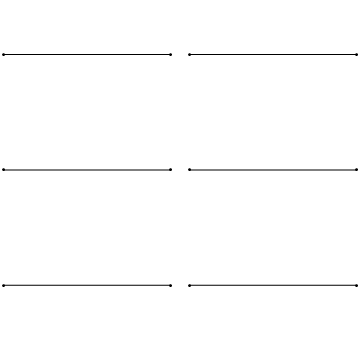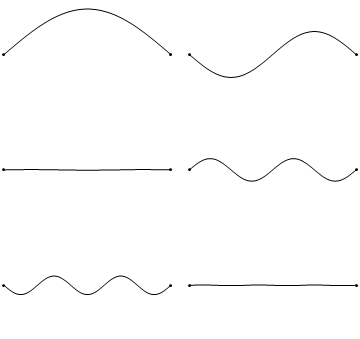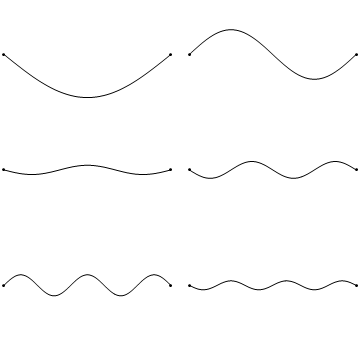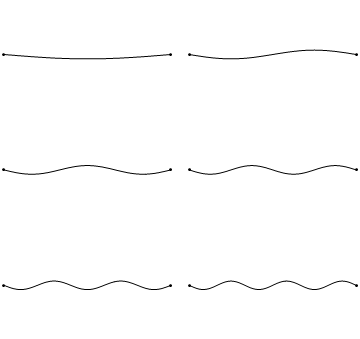
Dado que la aceleración de la amplitud de onda (lado derecho de la Ecuación\(\ref{2.1.1}\)) es proporcional a\(\dfrac{\partial^2}{\partial x^2}\), la mayor curvatura en el material produce una mayor aceleración, es decir, mayor velocidad cambiante de la onda (Figura 2.1.4 ) y mayor frecuencia de oscilación. Como se discutió más adelante, las ondas de mayor frecuencia (i.. e, más nodos) son soluciones de mayor energía; esto como se esperaba de los experimentos discutidos en el Capítulo 1 incluyendo la ecuación de Plank\(E=h\nu\).
Resumen
Ondas que exhiben movimiento y se propagan a través del tiempo y el espacio. Los dos tipos básicos de ondas son viajeras y estacionarias. Ambos exhiben propiedades onduladas y estructura (presencia de crestas y depresiones) que pueden ser descritas matemáticamente por una función de onda o amplitud. Ambos tipos de onda muestran movimiento (desplazamiento hacia arriba y hacia abajo), pero de diferentes maneras.Las olas viajeras tienen crestas y canales que se mueven constantemente de un punto a otro a medida que viajan sobre una longitud o distancia. De esta manera, la energía se transmite a lo largo de una onda viajera. En contraste, las ondas estacionarias tienen nodos en posiciones fijas; esto significa que las crestas y depresiones de la ola también se ubican a intervalos fijos. Por lo tanto, las ondas estacionarias solo experimentan movimiento vibratorio (desplazamiento hacia arriba y hacia abajo) en estos intervalos establecidos; ningún movimiento o energía viaja a lo largo de la longitud de una onda estacionaria.
Colaboradores y Atribuciones
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)

