2.5: Estática

Cuando múltiples fuerzas actúan sobre un cuerpo, la suma (vectorial) de esas fuerzas da la fuerza neta, que es la fuerza que sustituimos en la segunda ley de movimiento de Newton para obtener la ecuación de movimiento del cuerpo. Si todas las fuerzas suman cero, no habrá aceleración, y el cuerpo conserva cualquier velocidad que tuviera antes. La estática es el estudio de objetos que actualmente no se mueven ni experimentan una fuerza neta, y así permanecen estacionarios. Se podría esperar que este estudio sea más fácil que el caso dinámico cuando los cuerpos experimentan una fuerza neta, pero eso solo depende del contexto. Imagínese, por ejemplo, una jarra llena de canicas: no se mueven, pero las fuerzas que actúan sobre las canicas ciertamente no son cero, y tampoco se distribuyen uniformemente.

Incluso si no hay fuerza neta, no hay garantía de que un objeto no exhiba movimiento: si las fuerzas se distribuyen de manera desigual a lo largo de un objeto extendido, puede comenzar a girar. Las rotaciones siempre ocurren alrededor de un punto estacionario, conocido como el pivote. Sólo una fuerza que tenga un componente perpendicular a la línea que conecta su punto de acción con el pivote (el brazo) puede hacer que un objeto gire. La aceleración angular correspondiente debida a la fuerza depende tanto de la magnitud de esa componente perpendicular como de la longitud del brazo, y se conoce como el momento de la fuerza o el par\(\tau\). Por lo tanto, la magnitud del par viene dada por\(Fr sin\theta\), donde\(F\) está la magnitud de la fuerza, r la longitud del brazo, y\(\theta\) el ángulo entre la fuerza y el brazo. Si escribimos el brazo como un vector r apuntando desde el pivote hasta el punto donde actúa la fuerza, encontramos que la magnitud del par es igual al producto cruzado de\(r\) y\(F\):

\[\boldsymbol{\tau}=\boldsymbol{r} \times \boldsymbol{F}\]

La dirección de rotación se puede encontrar mediante la regla de la derecha desde la dirección del par: si el pulgar de su mano derecha apunta a lo largo de la dirección de\(\tau\), entonces la dirección en la que se curvan los dedos será la dirección en la que gira el objeto debido a la acción de la fuerza correspondiente \(F\).

Estudiaremos las rotaciones en detalle en el Capítulo 5. Por ahora, nos interesa el caso de que no haya movimiento, ni lineal ni rotacional, lo que significa que las fuerzas y pares que actúan sobre nuestro objeto deben satisfacer la condición de estabilidad: para que un objeto extendido sea estacionario, tanto la suma de las fuerzas como la suma de los pares que actúan sobre él deben ser cero.

Ejemplo\(\PageIndex{1}\): Suspended Sign

Un signo de masa M cuelga suspendido de una varilla de masa m y longitud de\(L\) manera simétrica y de tal manera que los centros de masa del signo y la varilla se alinean muy bien (Figura\(\PageIndex{1a}\)). Un extremo de la varilla está anclado a una pared directamente, mientras que el otro está soportado por un alambre con una masa insignificante que se une a la misma pared a una distancia h por encima del anclaje.

Figura\(\PageIndex{1}\): Un signo suspendido (ejemplo de un cálculo en estática). a) Ajuste de problemas. (b) Diagrama de cuerpo libre.

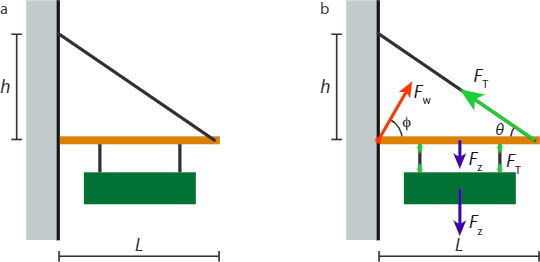
1. Si la tensión máxima que puede soportar el cable es T, encuentre el valor mínimo de h.
2. Para el caso de que la tensión en el cable sea igual a la tensión máxima, encuentre la fuerza (magnitud y dirección) ejercida por el anclaje sobre la varilla.

Solución

(a) Primero dibujamos un diagrama de cuerpo libre, Figura\(\PageIndex{1b}\). El balance de fuerzas en el letrero nos dice que las tensiones en los dos cables inferiores se suman a la fuerza gravitacional sobre el letrero. La varilla es estacionaria, por lo que sabemos que la suma de los pares sobre ella debe desaparecer. Para obtener pares, primero necesitamos un pivote; elegimos el punto donde la varilla está anclada a la pared. Luego tenemos tres fuerzas que contribuyen con un par en el sentido de las agujas del reloj y una que aporta un par en sentido contrario No nos dicen exactamente dónde están unidos los cables a la varilla, pero se nos dice que la configuración es simétrica y que el centro de masa del letrero se alinea con el de la varilla. Deje que el primer cable esté a una\(\alpha L\) distancia de la pared, y el segundo a una distancia\((1-\alpha)L\). El par total (en el sentido de las agujas del reloj) debido a la fuerza gravitacional en el signo y la varilla viene dado por:

\[\tau_{\mathrm{Z}}=\frac{1}{2} m g L+\frac{1}{2} M g \alpha L+\frac{1}{2} M g(1-\alpha) L=\frac{1}{2}(m+M) g L. \nonumber\]

El par en sentido contrario a las agujas del reloj proviene de la tensión en el cable, y viene dado por

\[\frac{1}{2} m g L+\frac{1}{2} M g \alpha L+\frac{1}{2} M g(1-\alpha) L=\frac{1}{2}(m+M) g L. \nonumber\]

Equiparar los dos pares nos permite resolver para tiene una función de\(F_T\), según lo solicitado, que da:

\[h^{2}=\left(\frac{1}{2} \frac{(m+M) g}{F_{\mathrm{T}}}\right)^{2}\left(h^{2}+L^{2}\right) \quad \rightarrow \quad h=\frac{(m+M) g L}{\sqrt{4 F_{\mathrm{T}}^{2}-(m+M)^{2} g^{2}}}\]

Encontramos el valor mínimo de h sustituyendo\(F_T=T_{max}\).

b) Como la varilla está estacionaria, todas las fuerzas sobre ella deben cancelarse. En la dirección horizontal, tenemos la componente horizontal de la tensión,\(T_{max}\cos \theta\) a la izquierda, que debe ser igual a la componente horizontal de la fuerza ejercida por la pared,\(F_w cos \phi\). En la dirección vertical, tenemos la fuerza gravitacional y las dos fuerzas de los cables sobre los que cuelga el signo en dirección descendente, y la componente vertical de la tensión en el alambre en dirección ascendente, cuya suma debe ser igual a la componente vertical de la fuerza ejercida por la pared (que puede apuntar hacia arriba o hacia abajo). Por lo tanto, tenemos

\[\begin{align*} F_{\mathrm{w}} \cos \phi &=T_{\max } \cos \theta \\[4pt] F_{\mathrm{w}} \sin \phi &=(m+M) g+T_{\max } \sin \theta \end{align*}\]

donde\(\tan \theta={h \over L}\) y\(h\) se da en la respuesta a la letra a). Nos encontramos con que

\[\begin{align*} F_{\mathrm{w}}^{2} &=T_{\mathrm{max}}^{2}+2(m+M) g T_{\max } \sin \theta+(m+M)^{2} g^{2} \\[4pt] \tan \phi &=\frac{T_{\max } \cos \theta}{(m+M) g+T_{\max } \sin \theta} \end{align*}\]

Tenga en cuenta que las expresiones anteriores dan la respuesta completa (magnitud y dirección). Podríamos eliminar\(h\) y\(\theta\), pero eso solo sería álgebra, lo que lleva a expresiones más complicadas, y no muy útiles en sí misma.Si nos hubieran pedido que calculáramos la altura o fuerza por cualquier valor específico de M, m y L, podríamos obtener las respuestas fácilmente sustituyendo los números en el expresiones dadas aquí.