9.4: Apéndice 9A El Campo Gravitacional de una Cáscara Esférica de Materia.

Al analizar las interacciones gravitacionales entre cuerpos esféricos uniformes asumimos que podríamos tratar cada esfera como una masa puntual ubicada en el centro de la esfera y luego usar la Ley Universal de Gravitación para determinar la fuerza entre los dos objetos puntiformes. Ahora justificaremos esa suposición. Para simplificar solo necesitamos considerar la interacción entre un objeto esférico y una masa puntiforme. Nos gustaría determinar la fuerza gravitacional sobre el objeto puntual de masa\(m_{1}\) debido a la interacción gravitacional con una esfera sólida y uniforme de masa\(m_{2}\) y radio R. Para determinar la ley de fuerza primero consideraremos la interacción entre el objeto puntiforme y una capa esférica uniforme de masa\(m_{s}\) y radio R. Mostraremos que:

1) La fuerza gravitacional que actúa sobre un objeto puntual de masa\(m_{1}\) ubicado a una distancia r > R del centro de una concha esférica uniforme de masa\(m_{s}\) y radio R es la misma fuerza que surgiría si toda la masa de la concha se colocara en el centro de la concha.

2) La fuerza gravitacional sobre un objeto de masa\(m_{1}\) colocado dentro de una capa esférica de materia es cero.

La ley de fuerza resume estos resultados:

\ [\ overrightarrow {\ mathbf {F}} _ {s, 1} (r) =\ left\ {\ begin {array} {cc}
-G\ frac {m_ {s} m_ {1}} {r^ {2}}\ hat {\ mathbf {r}}, & r>r\\ overrightarrow {\ mathbf {0}}, & r>r\\ overrightarrow {
\ mathbf {0}}, & r>r\\ overrightarrow {\ mathbf {<R
\ end {array}\ right. \ nonumber\]

donde\(\hat{\mathbf{r}}\) está el vector unitario ubicado en la posición del objeto y apuntando radialmente lejos del centro de la concha.

Para una distribución esférica uniforme de la materia, podemos dividir la esfera en conchas delgadas. Entonces la fuerza entre el objeto puntiforme y cada proyectil es la misma que si toda la masa del proyectil estuviera colocada en el centro del proyectil. Luego sumamos todas las contribuciones de las conchas (integración), la distribución esférica puede ser tratada como un objeto puntiforme ubicado en el centro de la esfera justificando nuestra suposición.

Por lo tanto, basta con analizar el caso de la concha esférica. Primero dividiremos el proyectil en elementos de área pequeña y calcularemos la fuerza gravitacional sobre el objeto puntiforme debido a un elemento del caparazón y luego agregaremos las fuerzas debidas a todos estos elementos mediante la integración.

Comenzamos por elegir un sistema de coordenadas. Elija nuestro eje z para ser dirigido desde el centro de la esfera a la posición del objeto, en la posición\(\overrightarrow{\mathbf{r}}=z \hat{\mathbf{k}}\), de modo que\(z \geq 0\) (la Figura 9A.1 muestra el objeto que se encuentra fuera del caparazón con\(z>R\))

Figura 9A.1 Objeto que se encuentra fuera del caparazón con\(z>R\)

Elija coordenadas esféricas como se muestra en la Figura 9A.2.

Figura 9A.2 Coordenadas esféricas

Para un punto en la superficie de una esfera de radio r = R, las coordenadas cartesianas están relacionadas con las coordenadas esféricas por

\ [\ begin {array} {l}
x=R\ sin\ theta\ cos\ phi\
y=R\ sin\ theta\ sin\ phi\
z=R\ cos\ theta
\ end {array}\ nonumber\]

dónde\(0 \leq \theta \leq \pi\) y\(0 \leq \phi \leq 2 \pi\).

Obsérvese que el ángulo θ en la Figura 9A.2 y Ecuaciones (9.A.1) no es el mismo que en coordenadas polares planas o coordenadas cilíndricas. El ángulo θ se conoce como la colatitud, el complemento de la latitud. Ahora elegimos un elemento de área pequeña que se muestra en la Figura 9A.3.

Figura 9A.3 Elemento de área infinitesimal

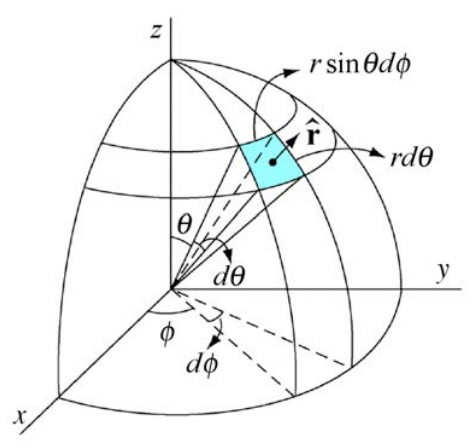
El elemento de área infinitesimal en la superficie de la concha viene dado por

\[d a=R^{2} \sin \theta d \theta d \phi \nonumber \]

Entonces la masa dm contenida en ese elemento es

\[d m=\sigma d a=\sigma R^{2} \sin \theta d \theta d \phi \nonumber \]

donde\(\sigma\) es la densidad de masa superficial dada por

\[\sigma=m_{s} / 4 \pi R^{2} \nonumber \]

La fuerza gravitacional\(\overrightarrow{\mathbf{F}}_{d m, m_{1}}\) sobre el objeto de masa\(m_{1}\) que se encuentra fuera del caparazón debido a la pieza infinitesimal de la concha (con masa dm) se muestra en la Figura 9A.4.

Figura 9A.4 Fuerza sobre un objeto puntiforme debido a una pieza de proyectil

La contribución de la pieza con masa dm a la fuerza gravitacional sobre el objeto de masa\(m_{1}\) que se encuentra fuera del caparazón tiene una componente que apunta en la\(\hat{\mathbf{k}}\) dirección negativa y una componente que apunta radialmente lejos del eje z. Por simetría hay otro elemento de masa con la misma masa diferencial\(d m^{\prime}=d m\) en el otro lado de la concha con la misma co-latitud θ pero con\(\phi\) reemplazado por\(\phi \pm \pi\); este reemplazo cambia el signo de x e y en las Ecuaciones (9.A.1) pero deja z sin cambios. Este otro elemento de masa produce una fuerza gravitacional que cancela exactamente la componente radial de la fuerza que apunta lejos del eje z. Por lo tanto, la suma de las fuerzas de estos elementos de masa diferencial sobre el objeto solo tiene un componente en la\(\hat{\mathbf{k}}\) dirección negativa (Figura 9A.5).

Figura 9A.5 Cancelación simétrica de componentes de fuerza

Por lo tanto, solo necesitamos el vector de componente z de la fuerza debido a la pieza del shell en el objeto punto-como.

Figura 9A.6 Geometría para calcular la fuerza debida a pieza de concha.

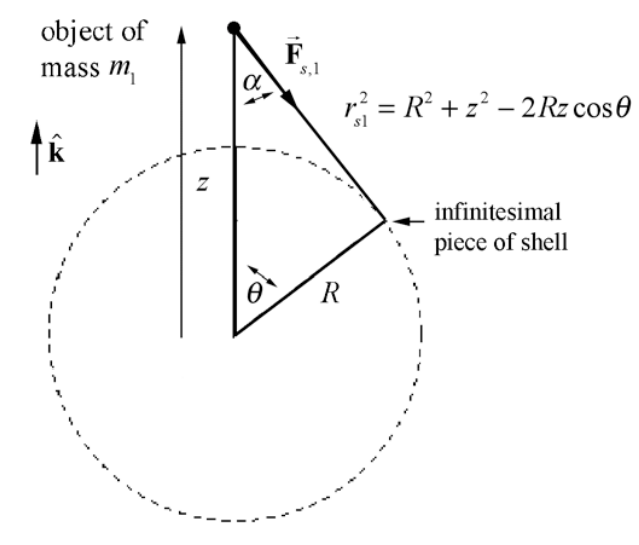
A partir de la geometría de la puesta a punto (Figura 9A.6) vemos que

\[\left(d \overrightarrow{\mathbf{F}}_{s, 1}\right)_{z} \equiv d F \hat{\mathbf{k}}=-G \frac{m_{1} d m}{r_{s 1}^{2}} \cos \alpha \hat{\mathbf{k}} \nonumber \]

Así

\[d F_{z}=-G \frac{m_{1} d m}{r_{s 1}^{2}} \cos \alpha=-\frac{G m_{s} m_{1}}{4 \pi} \frac{\cos \alpha \sin \theta d \theta d \phi}{r_{s 1}^{2}} \nonumber \]

La integral de la fuerza sobre la superficie es entonces

\[F_{z}=-G m_{1} \int_{\theta=0}^{\theta=\pi \phi=2 \pi} \int_{\phi=0} \frac{d m \cos \alpha}{r_{s 1}^{2}}=-\frac{G m_{s} m_{1}^{\theta=\pi \phi=2 \pi}}{4 \pi} \int_{\theta=0}^{\infty} \int_{\phi=0} \frac{\cos \alpha \sin \theta d \theta d \phi}{r_{s 1}^{2}} \nonumber \]

La\(\phi\) integral es un rendimiento directo

\[F_{z}=-\frac{G m_{s} m_{1}^{\theta=\pi}}{2} \int_{\theta=0}^{\cos \alpha \sin \theta d \theta} \nonumber \]

De la Figura 9A.6 podemos utilizar la ley de los cosenos de dos maneras diferentes

\ [\ begin {array} {l}
r_ {s 1} ^ {2} =R^ {2} +z^ {2} -2 R z\ cos\ theta\\
R^ {2} =z^ {2} +r_ {s 1} ^ {2} -2 r_ {s, 1} z\ cos\ alfa
\ end {array}\ nonumber\]

Diferenciando la primera expresión en (9.A.5), con rendimientos constantes R y z,

\[2 r_{s, 1} d r_{s, 1}=2 R z \sin \theta d \theta \nonumber \]

De ahí

\[\sin \theta d \theta=\frac{r_{s, 1}}{R z} d r_{s, 1} \nonumber \]

y de la segunda expresión en (9.A.5) tenemos que

\[\cos \alpha=\frac{1}{2 z r_{s, 1}}\left[\left(z^{2}-R^{2}\right)+r_{s 1}^{2}\right] \nonumber \]

Ahora tenemos todo lo que necesitamos en cuanto a\(r_{s, 1}\).

Para el caso cuando\(z>R, r_{s, 1}\) varía de z − R a z + R. Sustituyendo las ecuaciones (9.A.7) y (9.A.8) a la ecuación (9.A.3) y usando los límites para los rendimientos integrales definidos

\ [\ begin {alineado}
F_ {z} &=-\ frac {G m_ {s} m_ {1} ^ {\ theta=\ pi}} {2}\ int_ {\ theta=0} ^ {\ cos\ alfa\ sin\ theta} d\ theta\
&=-\ frac {G m_ {s} m_ {1}} {2}\ frac {1} {2 z}\ int_ {z-R} ^ {z+r}\ frac {1} {r_ {s, 1}}\ izquierda [\ izquierda (z^ {2} -R^ {2}\ derecha) +r_ {s, 1} ^ {2}\ derecha]\ frac {1} {r_ {s, 1} ^ {2}\ frac {r_ {s, 1} d r_ {s, 1}} {R z}\\
&=-\ frac {G m_ {s} m_ {1}} {2}\ frac {1} {2 R z^ {2}}\ izquierda [\ izquierda (z^ {2} -R^ {2}\ derecha)\ int_ {z-R} ^ {z+r}\ frac {d r_ {s, 1}} {r_ {s, 1} ^ {2}} +\ int_ {z-R} ^ {z+r} d r_ {s, 1}\ derecha]
\ final {alineado}\ nonumber\]

No se deben necesitar tablas para estos; el resultado es

\ [\ begin {alineado}
F_ {z} &=-\ frac {G m_ {s} m_ {1}} {2}\ frac {1} {2} {2 R z^ {2}}\ izquierda [-\ frac {\ izquierda (z^ {2} -R^ {2}\ derecha)} {r_ {s, 1}} +r_ {s, 1} derecha] _ {z-R} ^ {z+R}\\
&=-\ frac {G m_ {s} m_ {1}} {2}\ frac {1} {2 R z^ {2}} [- (z-R) + (z+r) +2 R]\\
&=-\ frac {G m_ {s} m_ {1}} {z^ {2}
\ end {alineado}\ nonumber\]

Para el caso cuando\(z<R, r_{s, 1}\) varía de R − z a R + z. Entonces la integral es

\ [\ begin {alineado}
F_ {z} &=-\ frac {G m_ {s} m_ {1}} {2}\ frac {1} {2} {2 R z^ {2}}\ izquierda [-\ frac {\ izquierda (z^ {2} -R^ {2}\ derecha)} {r_ {s, 1}} +r_ {s, 1} derecha] _ {R-z} ^ {r+z}\\
&=-\ frac {G m_ {s} m_ {1}} {2}\ frac {1} {2 R z^ {2}} [- (z-R) - (z+r) +2 z]\\
&=0
\ end {alineado}\ nonumber\]

Así que hemos demostrado la proposición de que para un objeto puntiforme ubicado en el eje z a una distancia z del centro de una concha esférica, la fuerza gravitacional sobre el objeto tipo punto viene dada por

\ [\ overrightarrow {\ mathbf {F}} _ {s, 1} (r) =\ izquierda\ {\ begin {alineado}
-G\ frac {m_ {s} m_ {1}} {z^ {2}}\ hat {\ mathbf {k}}, & z>R\
\ overrightarrow {\ mathbf {0}}, & z<r
\ fin {alineado}\ derecho. \ nonumber\]

Esto demuestra el resultado de que la fuerza gravitacional dentro del proyectil es cero y la fuerza gravitacional fuera del proyectil equivale a poner toda la masa en el centro del proyectil.