14.9: Ejemplos trabajados

Ejemplo 14.2 Velocidad de escape de Toro

El asteroide Toro, descubierto en 1964, tiene un radio de aproximadamente\(R=5.0 \mathrm{km}\) y una masa de aproximadamente\(m_{t}=2.0 \times 10^{15} \mathrm{kg}\). Supongamos que Toro es una esfera perfectamente uniforme. ¿Cuál es la velocidad de escape para un objeto de masa m en la superficie de Toro? ¿Podría una persona alcanzar esta velocidad (en la tierra) corriendo?

Solución: La única energía potencial en este problema es la energía potencial gravitacional. Elegimos el punto cero para que la energía potencial sea cuando el objeto y Toro están a una distancia infinita,\(U^{G}(\infty) \equiv 0\). Con esta elección, la energía potencial cuando el objeto y Toro están a una distancia finita r separados viene dada por

\[U^{G}(r)=-\frac{G m_{t} m}{r} \nonumber \]

con\(U^{G}(\infty) \equiv 0\) La expresión velocidad de escape se refiere a la velocidad mínima necesaria para que un objeto escape de la interacción gravitacional del asteroide y se desplace a una distancia infinita. Si el objeto tiene una velocidad menor que la velocidad de escape, no podrá escapar de la fuerza gravitacional y deberá regresar a Toro. Si el objeto tiene una velocidad mayor que la velocidad de escape, tendrá una energía cinética distinta de cero al infinito. La condición para la velocidad de escape es que el objeto tendrá exactamente cero energía cinética en el infinito.

Elegimos nuestro estado inicial, en el momento\(t_{i}\), cuando el objeto está en la superficie del asteroide con una velocidad igual a la velocidad de escape. Elegimos nuestro estado final, en el momento\(t_{f}\), para que ocurra cuando la distancia de separación entre el asteroide y el objeto es infinita.

La energía cinética inicial es\(K_{i}=(1 / 2) m v_{\mathrm{esc}}^{2}\). La energía potencial inicial es\(U_{i}=-G m_{t} m / R\) y así la energía mecánica inicial es

\[E_{i}=K_{i}+U_{i}=\frac{1}{2} m v_{\mathrm{esc}}^{2}-\frac{G m_{t} m}{R} \nonumber \]

La energía cinética final es\(K_{f}=0\) porque esta es la c

ondition que define la velocidad de escape. La energía potencial final es cero,\(U_{f}=0\) porque elegimos el punto cero para la energía potencial en el infinito. La energía mecánica final es entonces

\[E_{f}=K_{f}+U_{f}=0 \nonumber \]

No hay trabajo no conservador, por lo que el cambio en la energía mecánica es cero

\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]

Por lo tanto

\[0=-\left(\frac{1}{2} m v_{\mathrm{esc}}^{2}-\frac{G m_{t} m}{R}\right) \nonumber \]

Esto se puede resolver para la velocidad de escape,

\ [\ begin {alineado}
v_ {\ mathrm {esc}} &=\ sqrt {\ frac {2 G m_ {t}} {R}}\\
&=\ sqrt {\ frac {2\ left (6.67\ veces 10^ {-11}\ mathrm {N}\ cdot\ mathrm {m} ^ {2}\ cdot\ mathrm {kg} ^ {-2}\ derecha)\ izquierda (2.0\ veces 10^ {15}\ mathrm {kg}\ derecha)} {\ izquierda (5.0\ veces 10^ {3}\ mathrm {m}\ derecha)}} =7.3\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}
\ final {alineado}\ nonumber\]

Teniendo en cuenta que los velocistas olímpicos suelen alcanzar velocidades de\(12 \mathrm{m} \cdot \mathrm{s}^{-1}\), esta es una velocidad fácil de alcanzar corriendo en la tierra. Puede ser más difícil para Toro generar la aceleración necesaria para alcanzar esta velocidad empujando del suelo, ya que cualquier ligera fuerza ascendente elevará el centro de masa del corredor y tardará sustancialmente más tiempo que en la tierra en volver a bajar para otro empuje del suelo.

Ejemplo 14.3 Spring-blok-loop-the-loop

Un pequeño bloque de masa m se empuja contra un resorte con constante de resorte k y se mantiene en su lugar con una captura. El resorte se comprime a una distancia desconocida x (Figura 14.12). Cuando se retira el retén, el bloque sale del muelle y se desliza a lo largo de un bucle circular sin fricción de radio r. Cuando el bloque alcanza la parte superior del bucle, la fuerza del bucle sobre el bloque (la fuerza normal) es igual al doble de la fuerza gravitacional sobre la masa. (a) Utilizando la conservación de energía, encontrar la energía cinética del bloque en la parte superior del bucle. (b) Utilizando la Segunda Ley de Newton, derivar la ecuación de movimiento para el bloque cuando está en la parte superior del bucle. Específicamente, encuentra la velocidad\(v_{\text {top }}\) en términos de la constante de gravitación g y el radio de bucle r. c) ¿Qué distancia se comprimió el muelle?

Figura 14.12 Estado inicial para el sistema de resorte-bloque-bucl-el-bucle

Solución: a) Elija para el estado inicial el instante antes de que se libere la captura. La energía cinética inicial es\(K_{i}=0\). La energía potencial inicial es distinta de cero,\(U_{i}=(1 / 2) k x^{2}\). La energía mecánica inicial es entonces

\[E_{i}=K_{i}+U_{i}=\frac{1}{2} k x^{2} \nonumber \]

Elija para el estado final en el instante en que el bloque esté en la parte superior del bucle. La energía cinética final es\(K_{f}=(1 / 2) m v_{\text {top }}^{2}\); el bloque está en movimiento con la velocidad\(v_{\text {top }}\). La energía potencial final es distinta de cero,\(U_{f}=(m g)(2 R)\). La energía mecánica final es entonces

\[E_{f}=K_{f}+U_{f}=2 m g R+\frac{1}{2} m v_{\mathrm{top}}^{2} \nonumber \]

Debido a que estamos asumiendo que la pista es sin fricción y descuidando la resistencia al aire, no hay ningún trabajo no conservador. Por lo tanto, el cambio en la energía mecánica es cero,

\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]

La energía mecánica se conserva\(E_{f}=E_{i}\), por lo tanto

\[2 m g R+\frac{1}{2} m v_{\mathrm{top}}^{2}=\frac{1}{2} k x^{2} \nonumber \]

De la Ecuación (14.8.10), la energía cinética en la parte superior del bucle es

\[\frac{1}{2} m v_{\mathrm{top}}^{2}=\frac{1}{2} k x^{2}-2 m g R \nonumber \]

b) En la parte superior del bucle, las fuerzas sobre el bloque son la fuerza gravitacional de magnitud mg y la fuerza normal de magnitud N, ambas dirigidas hacia abajo. La Segunda Ley de Newton en la dirección radial, que es la dirección descendente, es

\[-m g-N=-\frac{m v_{\mathrm{top}}^{2}}{R} \nonumber \]

En este problema, se nos da que cuando el bloque alcanza la parte superior del bucle, la fuerza del bucle sobre el bloque (la fuerza normal, hacia abajo en este caso) es igual al doble del peso del bloque, N = 2mg. La Segunda Ley, la Ecuación (14.8.12), luego se convierte

\[3 m g=\frac{m v_{\mathrm{top}}^{2}}{R} \nonumber \]

Podemos reescribir la Ecuación (14.8.13) en términos de la energía cinética como

\[\frac{3}{2} m g R=\frac{1}{2} m v_{\mathrm{top}}^{2} \nonumber \]

Por lo tanto, la velocidad en la parte superior es

\[v_{\mathrm{top}}=\sqrt{3 m g R} \nonumber \]

c) Ecuaciones de Peinado (14.8.11) y (14.8.14) Rendimientos

\[\frac{7}{2} m g R=\frac{1}{2} k x^{2} \nonumber \]

Así, el desplazamiento inicial del resorte desde el equilibrio es

\[x=\sqrt{\frac{7 m g R}{k}} \nonumber \]

Ejemplo 14.4 Muelle masivo sobre una superficie rugosa

Un bloque de masa m se desliza a lo largo de una mesa horizontal con velocidad\(v_{0}\). A x = 0 golpea un resorte con constante de resorte k y comienza a experimentar una fuerza de fricción. El coeficiente de fricción es variable y viene dado por\(\mu=b x\), donde b es una constante positiva. Encuentra la pérdida de energía mecánica cuando el bloque primero viene a descansar momentáneamente.

Figura 14.13 Sistema de bloque de resorte

Solución: A partir del modelo dado para la fuerza de fricción, podríamos encontrar el trabajo no conservador realizado, que es lo mismo que la pérdida de energía mecánica, si conociéramos la posición\(x_{f}\) donde primero descansa el bloque. La forma más directa (y más fácil) de encontrar\(x_{f}\) es usar el teorema trabajo-energía. La energía mecánica inicial es\(E_{i}=m v_{i}^{2} / 2\) y la energía mecánica final es\(E_{f}=k x_{f}^{2} / 2\) (tenga en cuenta que no hay término de energía potencial en\(E_{i}\) y ningún término de energía cinética\(E_{f}\) La diferencia entre estas dos energías mecánicas es el trabajo no conservador realizado por la fuerza de fricción,

\ [\ begin {alineado}
W_ {\ mathrm {nc}} &=\ int_ {x=0} ^ {x=x_ {f}} F_ {\ mathrm {nc}} d x=\ int_ {x=0} ^ {x=x_ {f}} -F_ {\ mathrm {fricción}} d x=\ int_ {x=0} ^ x_ {f}} -\ mu N d x\\
&=-\ int_ {0} ^ {x_ {f}} b x m g d x=-\ frac {1} {2} b m g x_ {f} ^ {2}
\ final {alineado}\ nonumber\]

Entonces tenemos eso

\ [\ begin {alineado}
W_ {\ mathrm {nc}} &=\ Delta E_ {m}\\
W_ {\ mathrm {nc}} &=E_ {f} -E_ {i}\\
-\ frac {1} {2} b m g x_ {f} ^ {2} &=\ frac {1} {2} k x_ {f} ^ 2} -\ frac {1} {2} m v_ {i} ^ {2}
\ final {alineado}\ nonumber\]

Resolviendo la última de estas ecuaciones para\(x_{f}^{2}\) rendimientos

\[x_{f}^{2}=\frac{m v_{0}^{2}}{k+b m g} \nonumber \]

La ecuación sustituta (14.8.20) en la ecuación (14.8.18) da el resultado de que

\[W_{\mathrm{nc}}=-\frac{b m g}{2} \frac{m v_{0}^{2}}{k+b m g}=-\frac{m v_{0}^{2}}{2}\left(1+\frac{k}{b m g}\right)^{-1} \nonumber \]

Vale la pena comprobar que el resultado anterior es dimensionalmente correcto. A partir del modelo, el parámetro b debe tener dimensiones de longitud inversa (el coeficiente de fricción\(\mu\) debe ser adimensional), y así el producto bmg tiene dimensiones de fuerza por longitud, al igual que la constante de resorte k; el resultado es dimensionalmente consistente.

Ejemplo 14.5 Muelle de carro en un plano inclinado

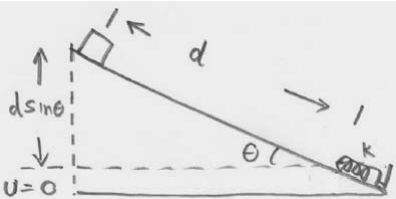
Un objeto de masa m se desliza hacia abajo por un plano que está inclinado en un ángulo θ desde la horizontal (Figura 14.14). El objeto comienza en reposo. El centro de masa del carro está a una distancia d de un resorte no estirado que se encuentra en la parte inferior del avión. Supongamos que el resorte es sin masa, y tiene una constante de resorte k. Supongamos que el plano inclinado es sin fricción. a) ¿Hasta dónde se comprimirá el resorte cuando la masa llegue a descansar por primera vez? (b) Ahora supongamos que el plano inclinado tiene un coeficiente de fricción cinética\(\mu_{\mathrm{k}}\) ¿Hasta dónde se comprimirá el resorte cuando la masa llegue a descansar por primera vez? La fricción es principalmente entre las ruedas y los cojinetes, no entre el carro y el plano, sino que la fuerza de fricción puede ser modelada por un coeficiente de fricción\(\mu_{\mathrm{k}}\). c) En el caso b) ¿cuánta energía se ha perdido por fricción?

Figura 14.14 Carrito en plano inclinado

Solución: Dejar x denotar el desplazamiento del resorte desde la posición de equilibrio. Elija el punto cero para la energía potencial gravitacional\(U^{g}(0)=0\) no en la parte inferior del plano inclinado, sino en la ubicación del extremo del resorte sin estirar. Elija el punto cero para la energía potencial del resorte donde el resorte está en su posición de equilibrio,\(U^{s}(0)=0\)

a) Elija para el estado inicial en el instante en que se libera el objeto (Figura 14.15). La energía cinética inicial es\(K_{i}=0\). La energía potencial inicial es distinta de cero,\(U_{i}=m g d \sin \theta\). La energía mecánica inicial es entonces

\[E_{i}=K_{i}+U_{i}=m g d \sin \theta \nonumber \]

Elija para el estado final el instante en que el objeto llegue a descansar por primera vez y el resorte se comprima una distancia x en la parte inferior del plano inclinado (Figura 14.16). La energía cinética final es\(K_{f}=0\) ya que la masa no está en movimiento. La energía potencial final es distinta de cero,\(U_{f}=k x^{2} / 2-x m g \sin \theta\) Observe que la energía potencial gravitacional es negativa porque el objeto ha caído por debajo de la altura del punto cero de la energía potencial gravitacional.

Figura 14.15 Estado inicial

Figura 14.16 Estado final

La energía mecánica final es entonces

\[E_{f}=K_{f}+U_{f}=\frac{1}{2} k x^{2}-x m g \sin \theta \nonumber \]

Debido a que estamos asumiendo que la pista es sin fricción y descuidando la resistencia al aire, no hay ningún trabajo no conservador. Por lo tanto, el cambio en la energía mecánica es cero,

\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]

Por lo tanto

\[d m g \sin \theta=\frac{1}{2} k x^{2}-x m g \sin \theta \nonumber \]

Esta es una ecuación cuadrática en x,

\[x^{2}-\frac{2 m g \sin \theta}{k} x-\frac{2 d m g \sin \theta}{k}=0 \nonumber \]

En la fórmula cuadrática, queremos la elección positiva de raíz cuadrada para la solución para asegurar un desplazamiento positivo del resorte desde el equilibrio,

\ [\ begin {alineado}
x &=\ frac {m g\ sin\ theta} {k} +\ izquierda (\ frac {m^ {2} g^ {2}\ sin ^ {2}\ theta} {k^ {2}} +\ frac {2 d m g\ sin\ theta} {k}\ derecha) ^ {1/2}\
&=\ frac {m g} {k} (\ sin\ theta+\ sqrt {1+2 (k d/m g)\ sin\ theta})
\ final {alineado}\ nonumber\]

(¿Qué representaría la solución con la raíz negativa?)

b) El efecto de la fricción cinética es que ahora hay un trabajo no conservador distinto de cero realizado sobre el objeto, que se ha movido una distancia,\(d+x\), dado por

\[W_{\mathrm{nc}}=-f_{\mathrm{k}}(d+x)=-\mu_{\mathrm{k}} N(d+x)=-\mu_{\mathrm{k}} m g \cos \theta(d+x) \nonumber \]

Observe que la fuerza normal se encuentra usando la Segunda Ley de Newton en la dirección perpendicular al plano inclinado,

\[N-m g \cos \theta=0 \nonumber \]

Por lo tanto, el cambio en la energía mecánica es

\[W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]

que se convierte

\[-\mu_{\mathrm{k}} m g \cos \theta(d+x)=\left(\frac{1}{2} k x^{2}-x m g \sin \theta\right)-d m g \sin \theta \nonumber \]

La ecuación (14.8.31) simplifica a

\[0=\left(\frac{1}{2} k x^{2}-x m g\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)\right)-d m g\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right) \nonumber \]

Esto es lo mismo que la Ecuación (14.8.25) anterior, pero con\(\sin \theta \rightarrow \sin \theta-\mu_{k} \cos \theta\). El desplazamiento máximo del resorte es cuando hay fricción es entonces

\[x=\frac{m g}{k}\left(\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)+\sqrt{1+2(k d / m g)\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)}\right) \nonumber \]

c) La energía perdida por fricción viene dada por\(W_{\mathrm{nc}}=-\mu_{\mathrm{k}} m g \cos \theta(d+x)\) donde x se da en la parte b).

Ejemplo 14.6 Deslizamiento de objetos sobre una esfera

Un punto pequeño como objeto de masa m descansa sobre una esfera de radio R. El objeto se libera de la parte superior de la esfera con una velocidad insignificante y lentamente comienza a deslizarse (Figura 14.17). Dejar que g denote la constante de gravitación. a) Determinar el ángulo\(\theta_{1}\) con respecto a la vertical en la que el objeto perderá contacto con la superficie de la esfera. b) Cuál es la velocidad\(v_{1}\) del objeto en el instante en que pierde contacto con la superficie de la esfera.

Figura 14.17 Objeto que se desliza sobre la superficie de la esfera

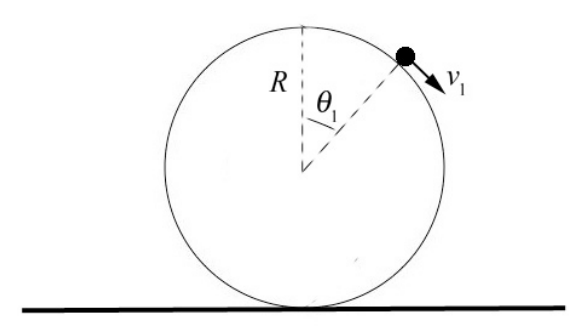
Solución: Comenzamos por identificar las fuerzas que actúan sobre el objeto. Hay dos fuerzas que actúan sobre el objeto, la gravitación y la fuerza radial normal que ejerce la esfera sobre la partícula que denotamos por N. Dibujamos un diagrama de fuerza de cuerpo libre para el objeto mientras se desliza sobre la esfera. Elegimos coordenadas polares como se muestra en la Figura 14.18.

Figura 14.18 Diagrama de fuerza de cuerpo libre en el objeto

La restricción clave es que cuando la partícula acaba de salir de la superficie la fuerza normal es cero,

\[N\left(\theta_{1}\right)=0 \nonumber \]

donde\(\theta_{1}\) denota el ángulo con respecto a la vertical en la que el objeto simplemente perderá contacto con la superficie de la esfera. Debido a que la fuerza normal es perpendicular al desplazamiento del objeto, no trabaja sobre el objeto y por lo tanto la conservación de energía no toma en cuenta la restricción al movimiento impuesta por la fuerza normal. Para analizar el efecto de la fuerza normal debemos utilizar el componente radial de la Segunda Ley de Newton,

\[N-m g \cos \theta=-m \frac{v^{2}}{R} \nonumber \]

Entonces, cuando el objeto simplemente pierde contacto con la superficie, las ecuaciones (14.8.34) y (14.8.35) requieren que

\[m g \cos \theta_{1}=m \frac{v_{1}^{2}}{R} \nonumber \]

donde\(v_{1}\) denota la velocidad del objeto en el instante en que pierde contacto con la superficie de la esfera. Tenga en cuenta que la ecuación de condición de restricción (14.8.36) se puede reescribir como

\[m g R \cos \theta_{1}=m v_{1}^{2} \nonumber \]

Ahora podemos aplicar la conservación de la energía. Elija el punto de referencia cero U = 0 para que la energía potencial sea el punto medio de la esfera.

Identificar el estado inicial como el instante en que se libera el objeto (Figura 14.19). Podemos descuidar la muy pequeña energía cinética inicial necesaria para alejar el objeto de la parte superior de la esfera y así\(K_{i}=0\). La energía potencial inicial es distinta de cero,\(U_{i}=m g R\). La energía mecánica inicial es entonces

\[E_{i}=K_{i}+U_{i}=m g R \nonumber \]

Figura 14.19 Estado inicial

Figura 14.20 Estado final

Elija para el estado final en el instante en que el objeto abandone la esfera (Figura 14.20). La energía cinética final es\(K_{f}=m v_{1}^{2} / 2\); el objeto está en movimiento con velocidad\(v_{1}\). La energía potencial final es distinta de cero,\(U_{f}=m g R \cos \theta_{1}\). La energía mecánica final es entonces

\[E_{f}=K_{f}+U_{f}=\frac{1}{2} m v_{1}^{2}+m g R \cos \theta_{1} \nonumber \]

Debido a que estamos asumiendo que la superficie de contacto es sin fricción y descuidando la resistencia al aire, no hay trabajo no conservador. Por lo tanto, el cambio en la energía mecánica es cero,

\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]

Por lo tanto

\[\frac{1}{2} m v_{1}^{2}+m g R \cos \theta_{1}=m g R \nonumber \]

Ahora resolvemos la condición de restricción Ecuación (14.8.37) en Ecuación (14.8.41) rendimiento

\[\frac{1}{2} m g R \cos \theta_{1}+m g R \cos \theta_{1}=m g R \nonumber \]

Ahora podemos resolver el ángulo en el que el objeto acaba de salir de la superficie

\[\theta_{1}=\cos ^{-1}(2 / 3) \nonumber \]

Ahora sustituimos este resultado por la Ecuación (14.8.37) y resolvemos para la velocidad

\[v_{1}=\sqrt{2 g R / 3} \nonumber \]