15.7: Colisiones bidimensionales en el marco de referencia del centro de masa

Colisión bidimensional en el marco de referencia del centro de masa

Considere la colisión elástica entre dos partículas en el marco de referencia de laboratorio (Figura 15.9). La partícula 1 de masa\(m_{1}\) se mueve inicialmente con velocidad\(\overrightarrow{\mathbf{v}}_{1, i}\) y choca elásticamente con una partícula 2 de masa\(m_{2}\) que inicialmente está en reposo. Después de la colisión, la partícula 1 se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{1, f}\) y la partícula 2 se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{2, f}\). En la sección 15.7.1 determinamos cómo encontrar\(v_{1, f}\),\(v_{2, f}\), y\(\theta_{2, f}\) en términos de\(v_{1, i}\) y\(\theta_{2, f}\). Ahora analizaremos la colisión en el marco de referencia del centro de masa, que se potencia desde el marco de laboratorio por la velocidad del centro de masa dada por\[\overrightarrow{\mathbf{v}}_{c m}=\frac{m_{1} \overrightarrow{\mathbf{v}}_{1, i}}{m_{1}+m_{2}} \nonumber \]

Debido a que asumimos que no hay fuerzas externas que actúen sobre el sistema, la velocidad del centro de masa permanece constante durante la interacción.

Figura 15.13 Colisión elástica bidimensional en el marco de referencia del centro de masa

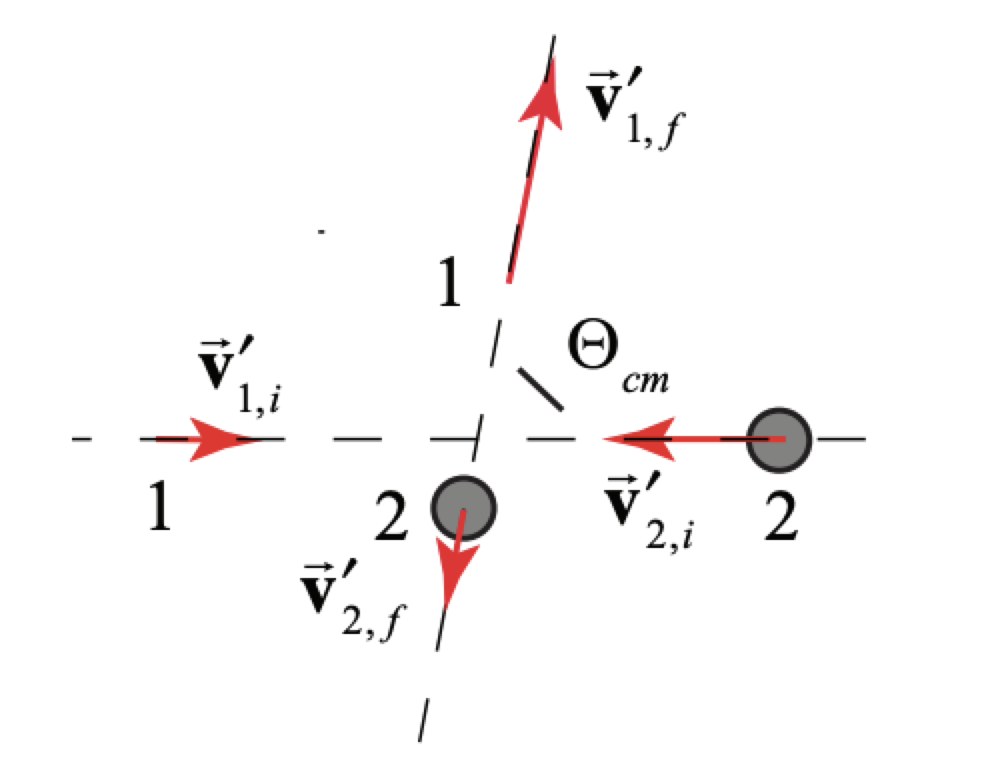
Recordemos que las velocidades de las partículas 1 y 2 en el marco del centro de masa están dadas por (Ecuación, (15.2.9) y (15.2.10)). En el marco de referencia del centro de masa las velocidades de las dos partículas entrantes están en direcciones opuestas, al igual que las velocidades de las dos partículas salientes después de la colisión (Figura 15.13). El ángulo\(\Theta_{c m}\) entre las velocidades entrante y saliente se denomina ángulo de dispersión del centro de masa.

Dispersión en el marco de referencia de centro de masa

Considera una colisión entre la partícula 1 de masa\(m_{1}\) y la velocidad\(\overrightarrow{\mathbf{v}}_{1, i}\) y la partícula 2 de masa\(m_{2}\) en reposo en el marco del laboratorio. La partícula 1 se dispersa elásticamente a través de un ángulo de dispersión\(\Theta\) en el marco de centro de masa. La velocidad del centro de masa viene dada por\[\overrightarrow{\mathbf{v}}_{c m}=\frac{m_{1} \overrightarrow{\mathbf{v}}_{1, i}}{m_{1}+m_{2}} \nonumber \]

En el marco de centro de masa, el impulso del sistema de dos partículas es cero\[\overrightarrow{\mathbf{0}}=m_{1} \overrightarrow{\mathbf{v}}_{1, i}^{\prime}+m_{2} \overrightarrow{\mathbf{v}}_{2, i}^{\prime}=m_{1} \overrightarrow{\mathbf{v}}_{1, f}^{\prime}+m_{2} \overrightarrow{\mathbf{v}}_{2, f}^{\prime} \nonumber \] Por lo tanto,\[\overrightarrow{\mathbf{v}}_{1, i}^{\prime}=-\frac{m_{2}}{m_{1}} \overrightarrow{\mathbf{v}}_{2, i}^{\prime} \nonumber \]\[\overrightarrow{\mathbf{v}}_{1, f}^{\prime}=-\frac{m_{2}}{m_{1}} \overrightarrow{\mathbf{v}}_{2, f}^{\prime} \nonumber \] la condición de energía en el marco de centro de masa es Ecuaciones de\[\frac{1}{2} m_{1} v_{1, i}^{\prime 2}+\frac{1}{2} m_{2} v_{2, i}^{\prime 2}=\frac{1}{2} m_{1} v_{1, f}^{\prime 2}+\frac{1}{2} m_{2} v_{2, f}^{\prime 2} \nonumber \] Sustitución (15.7.4) y (15.7.5) en Ecuación (15.7.6) rendimientos\[v_{1, i}^{\prime}=v_{1, f}^{\prime} \nonumber \] (solo estamos considerando magnitudes) . Por lo tanto,\[v_{2, i}^{\prime}=v_{2, f}^{\prime} \nonumber \] debido a que la magnitud de la velocidad de una partícula en el marco de referencia del centro de masa es proporcional a la velocidad relativa de las dos partículas, las ecuaciones (15.7.7) y (15.7.8) implican que la magnitud de la velocidad relativa tampoco cambia\[\left|\overrightarrow{\mathbf{v}}_{1,2, i}^{\prime}\right|=\left|\overrightarrow{\mathbf{v}}_{1,2, f}^{\prime}\right| \nonumber \] verificando nuestro anterior resultado que para una colisión elástica la velocidad relativa sigue siendo la misma, (Ecuación (15.2.20)). Sin embargo, la dirección de la velocidad relativa es girada por el ángulo de dispersión del centro de masa\(\Theta_{c m}\). Esto generaliza el principio energía-impulso a dos dimensiones. Recordemos que la velocidad relativa es independiente del marco de referencia,\[\overrightarrow{\mathbf{v}}_{1, i}-\overrightarrow{\mathbf{v}}_{2, i}=\overrightarrow{\mathbf{v}}_{1, i}^{\prime}-\overrightarrow{\mathbf{v}}_{2, i}^{\prime} \nonumber \] En el marco de referencia de laboratorio\(\overrightarrow{\mathbf{v}}_{2, i}=\overrightarrow{\mathbf{0}}\), de ahí la velocidad relativa inicial es\(\overrightarrow{\mathbf{v}}_{1,2, i}^{\prime}=\overrightarrow{\mathbf{v}}_{1,2, i}=\overrightarrow{\mathbf{v}}_{1, i}\), y las velocidades en el marco de centro de masa de las partículas son entonces\[\overrightarrow{\mathbf{V}}_{1, i}^{\prime}=\frac{\mu}{m_{1}} \overrightarrow{\mathbf{v}}_{1, i} \nonumber \]\[\overrightarrow{\mathbf{v}}_{2, i}^{\prime}=-\frac{\mu}{m_{2}} \overrightarrow{\mathbf{v}}_{1, i} \nonumber \] Por lo tanto las magnitudes de las velocidades finales en el marco del centro de masa son\[v_{1, f}^{\prime}=v_{1, i}^{\prime}=\frac{\mu}{m_{1}} v_{1,2, i}^{\prime}=\frac{\mu}{m_{1}} v_{1,2, i}=\frac{\mu}{m_{1}} v_{1, i} \nonumber \]\[v_{2, f}^{\prime}=v_{2, i}^{\prime}=\frac{\mu}{m_{2}} v_{1,2, i}^{\prime}=\frac{\mu}{m_{2}} v_{1,2, i}=\frac{\mu}{m_{2}} v_{1, i} \nonumber \]

Ejemplo 15.8 Dispersión en los marcos de laboratorio y CM

La partícula 1 de masa\(m_{1}\) y velocidad\(\overrightarrow{\mathbf{v}}_{1, i}\) por una partícula de masa en\(m_{2}\) reposo en el marco de laboratorio se dispersa elásticamente a través de un ángulo de dispersión\(\Theta\) en el marco del centro de masa, (Figura 15.14). Encontrar (i) el ángulo de dispersión de la partícula entrante en el marco de laboratorio, (ii) la magnitud de la velocidad final de la partícula entrante en el marco de referencia de laboratorio, y (iii) la pérdida fraccional de energía cinética de la partícula entrante.

Figura 15.14 Dispersión en el laboratorio y marcos de referencia del centro de masa

Solución

i) Para determinar el ángulo de dispersión del centro de masa utilizamos la ley de transformación para las velocidades\[\overrightarrow{\mathbf{v}}_{1, f}^{\prime}=\overrightarrow{\mathbf{v}}_{1, f}-\overrightarrow{\mathbf{v}}_{c m} \nonumber \] En la Figura 15.15 se muestra la colisión en el marco del centro de masa junto con las velocidades finales del marco de laboratorio y los ángulos de dispersión.

Figura 15.15 Velocidades finales de partículas colisionantes

La descomposición vectorial de la Ecuación (15.7.15) produce\[v_{1, f} \cos \theta_{1, i}=v_{1, f}^{\prime} \cos \Theta_{c m}-v_{c m} \nonumber \]\[v_{1, f} \sin \theta_{1, i}=v_{1, f}^{\prime} \sin \Theta_{c m} \nonumber \] donde elegimos como nuestras direcciones la Ecuación de Dividir horizontal y vertical (15.7.17) por (15.7.16) rinde\[\tan \theta_{1, i}=\frac{v_{1, f} \sin \theta_{1, i}}{v_{1, f} \cos \theta_{1, i}}=\frac{v_{1, f}^{\prime} \sin \Theta_{c m}}{v_{1, f}^{\prime} \cos \Theta_{c m}-v_{c m}} \nonumber \] Porque\(v_{1, i}^{\prime}=v_{1, f}^{\prime}\), podemos reescribir la Ecuación (15.7.18) como\[\tan \theta_{1, i}=\frac{v_{1, i}^{\prime} \sin \Theta_{c m}}{v_{1, i}^{\prime} \cos \Theta_{c m}-v_{c m}} \nonumber \]

Ahora sustituimos las Ecuaciones (15.7.12) y\(v_{c m}=m_{1} v_{1, i} /\left(m_{1}+m_{2}\right)\) en la Ecuación (15.7.19) rindiendo\[\tan \theta_{1, i}=\frac{m_{2} \sin \Theta_{c m}}{\cos \Theta_{c m}-m_{1} / m_{2}} \nonumber \] Así, en el marco de laboratorio, la partícula 1 se dispersa por un ángulo\[\theta_{1, i}=\tan ^{-1}\left(\frac{m_{2} \sin \Theta_{c m}}{\cos \Theta_{c m}-m_{1} / m_{2}}\right) \nonumber \]

ii) Podemos calcular el cuadrado de la velocidad final en el marco del laboratorio\[\overrightarrow{\mathbf{v}}_{1, f} \cdot \overrightarrow{\mathbf{v}}_{1, f}=\left(\overrightarrow{\mathbf{v}}_{1, f}^{\prime}+\overrightarrow{\mathbf{v}}_{c m}\right) \cdot\left(\overrightarrow{\mathbf{v}}_{1, f}^{\prime}+\overrightarrow{\mathbf{v}}_{c m}\right) \nonumber \] que se convierte\[v_{1, f}^{2}=v_{1, f}^{\prime 2}+2 \overrightarrow{\mathbf{v}}_{1, f}^{\prime} \cdot \overrightarrow{\mathbf{v}}_{c m}+v_{c m}^{2}=v_{1, f}^{\prime 2}+2 v_{1, f}^{\prime} v_{c m} \cos \Theta_{c m}+v_{c m}^{2} \nonumber \]

Utilizamos el hecho de que\(v_{1, f}^{\prime}=v_{1, i}^{\prime}=\left(\mu / m_{1}\right) v_{1,2, i}=\left(\mu / m_{1}\right) v_{1, i}=\left(m_{2} / m_{1}+m_{2}\right) v_{1, i}\) para reescribir la Ecuación (15.7.23) como\[v_{1, f}^{2}=\left(\frac{m_{2}}{m_{1}+m_{2}}\right)^{2} v_{1, i}^{2}+2 \frac{m_{2} m_{1}}{\left(m_{1}+m_{2}\right)^{2}} v_{1, i} \cos \Theta_{c m}+\frac{m_{1}^{2}}{\left(m_{1}+m_{2}\right)^{2}} v_{1, i}^{2} \nonumber \] Así\[v_{1, f}=\frac{\left(m_{2}^{2}+2 m_{2} m_{1} \cos \Theta_{c m}+m_{1}^{2}\right)^{1 / 2}}{m_{1}+m_{2}} v_{1, i} \nonumber \]

(iii) El cambio fraccional en la energía cinética de la partícula 1 en el marco de laboratorio viene dado por También\[\frac{K_{1, f}-K_{1, i}}{K_{1, i}}=\frac{v_{1, f}^{2}-v_{1, i}^{2}}{v_{1, i}^{2}}=\frac{m_{2}^{2}+2 m_{2} m_{1} \cos \Theta_{c m}+m_{1}^{2}}{\left(m_{1}+m_{2}\right)^{2}}-1=\frac{2 m_{2} m_{1}\left(\cos \Theta_{c m}-1\right)}{\left(m_{1}+m_{2}\right)^{2}} \nonumber \] podemos determinar el ángulo de dispersión\(\Theta_{c m}\) en el marco de referencia del centro de masa a partir del ángulo\(\theta_{1, i}\) de dispersión de la partícula 1 en el laboratorio. Ahora reescribimos las relaciones de impulso como\[v_{1, f} \cos \theta_{1, i}+v_{c m}=v_{1, f}^{\prime} \cos \Theta_{c m} \nonumber \]\[v_{1, f} \sin \theta_{1, i}=v_{1, f}^{\prime} \sin \Theta_{c m} \nonumber \]

De manera similar al argumento anterior, tenemos ese\[\tan \Theta_{c m}=\frac{v_{1, f} \sin \theta_{1, f}}{v_{1, f} \cos \theta_{1, f}+v_{c m}} \nonumber \] Recordemos de nuestro análisis de la colisión en el marco de laboratorio que si especificamos uno de los cuatro parámetros\(v_{1, f}, v_{2, f}, \theta_{1, f}\) o\(v_{1, f}\) entonces podemos resolver para los otros tres en términos de los parámetros iniciales\(v_{1, i}\) y\(v_{2, i}\). Con esa advertencia, podemos usar la Ecuación (15.7.29) para determinar\(\Theta_{c m}\)