19.7: Momento angular y par para rotación de eje fijo

Hemos demostrado que, para la rotación de eje fijo, el componente del par que hace que la velocidad angular cambie es el análogo rotacional de la Segunda Ley de Newton,

$$\vec{\tau}_{S}^{\mathrm{ext}}=I_{S} \overrightarrow{\boldsymbol{\alpha}} \nonumber$$

Ahora veremos que se trata de un caso especial del resultado más general

$$\vec{\tau}_{S}^{\mathrm{ext}}=\frac{d}{d t} \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}} \nonumber$$

Considera un cuerpo rígido que gira alrededor de un eje fijo que pasa por el punto$S$ y toma el eje fijo de rotación para que sea el eje z. Recordemos que todos los puntos del cuerpo rígido giran alrededor del eje z con la misma velocidad angular$\vec{\omega}=(d \theta / d t) \hat{\mathbf{k}}=\omega_{z} \hat{\mathbf{k}}$. De manera similar, todos los puntos en el cuerpo rígido tienen la misma aceleración angular,$\overrightarrow{\boldsymbol{\alpha}}=\left(d^{2} \theta / d t^{2}\right) \hat{\mathbf{k}}=\alpha_{z} \hat{\mathbf{k}}$. Deje que el punto$S$ se encuentre en algún lugar a lo largo del eje z.

Como antes, el cuerpo se divide en elementos individuales. Calculamos la contribución de cada elemento al momento angular alrededor del punto$S$, y luego sumamos sobre todos los elementos. La suma se convertirá en una integral para un cuerpo continuo.

Cada elemento individual tiene una masa$\Delta m_{j}$ y se mueve en un círculo de radio$r_{S, j}^{\perp}$ alrededor del eje de rotación. Dejar$\overrightarrow{\mathbf{r}}_{S, j}$ ser el vector desde el punto$S$ hasta el elemento. El impulso del elemento,$\overrightarrow{\mathbf{p}}_{j}$, es tangente a este círculo (Figura 19.16).

Figura 19.16 Geometría de rotación instantánea.

El momento angular del$j^{t h}$ elemento alrededor del punto$S$ viene dado por$\overrightarrow{\mathbf{L}}_{S, j}=\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{p}}_{j}$. El vector se$\overrightarrow{\mathbf{r}}_{S, j}$ puede descomponer en componentes paralelos y perpendiculares con respecto al eje de rotación$\overrightarrow{\mathbf{r}}_{S, j}=\overrightarrow{\mathbf{r}}_{S, j}^{\|}+\overrightarrow{\mathbf{r}}_{S, j}^{\perp}$ (Figura 19.16), donde$r_{S, j}^{\perp}=\left|\overrightarrow{\mathbf{r}}_{S, j}^{\perp}\right| \text { and } r_{S, j}^{\|}=\left|\overrightarrow{\mathbf{r}}_{S, j}^{\|}\right|$. El impulso viene dado por$\overrightarrow{\mathbf{p}}_{j}=\Delta m_{j} r_{S, j}^{\perp} \omega_{z} \hat{\theta}$. Entonces el momento angular sobre el punto$S$ es

\ [\ begin {array} {l}
\ overrightarrow {\ mathbf {L}} _ {S, j} =\ overrightarrow {\ mathbf {r}} _ {S, j}\ veces\ overrightarrow {\ mathbf {p}} _ {j} =\ left (r_ {S, j} ^ {\ perp}\ sombrero {\ mathbf {r}} +r_ {S, j} ^ {\ |}\ sombrero {\ mathbf {k}}\ derecha)\ veces\ izquierda (\ Delta m_ {j} r_ {S, j} ^ {\ perp}\ omega_ {z}\ sombrero {\ theta}\ derecha)\\
=\ Delta m_ {j}\ izquierda (r_ {S, j} ^ {\ perp}\ derecha) ^ {2}\ omega_ {z} -\ Delta m_ {j} r_ {S, j} ^ {\ |} r_ {S, j} ^ {\ perp}\ omega_ {z}\ hat {\ mathumbbf {r}}
\ end {array}\ nona_ er\]

En la última expresión de la Ecuación (19.5.22), el segundo término tiene una dirección que es perpendicular al eje z. Por lo tanto el componente z del momento angular alrededor del punto$S$$\left(L_{S, j}\right)_{z}$,, surge enteramente del segundo término,$\overrightarrow{\mathbf{r}}_{S, j}^{\perp} \times \overrightarrow{\mathbf{p}}_{j}$. Por lo tanto, el componente z del momento angular$S$ es

$$\left(L_{S, j}\right)_{z}=\Delta m_{j}\left(r_{S, j}^{\perp}\right)^{2} \omega_{z} \nonumber$$

El componente z del momento angular del sistema$S$ es la suma sobre todos los elementos,

$$L_{S, z}^{\mathrm{ss}}=\sum_{j}\left(L_{s, j}\right)_{z}=\sum_{j} \Delta m_{j}\left(r_{s, j}^{\perp}\right)^{2} \omega_{z} \nonumber$$

Para una distribución continua de la masa, la suma se convierte en una integral sobre el cuerpo,

$$L_{S, z}^{\mathrm{sys}}=\int_{\mathrm{body}} d m\left(r_{d m}\right)^{2} \omega_{z} \nonumber$$

donde$r_{d m}$ es la distancia desde el eje z fijo hasta el elemento infinitesimal de masa dm. El momento de inercia de un cuerpo rígido alrededor de un eje z fijo que pasa a través de un punto$S$ viene dado por una integral sobre el cuerpo

$$I_{S}=\int_{\text {body }} d m\left(r_{d m}\right)^{2} \nonumber$$

Así, la componente z del momento angular alrededor$S$ para un eje fijo que pasa$S$ en la dirección z es proporcional a la componente z de la velocidad angular$\omega_{z}$,

$$L_{S, z}^{\mathrm{sys}}=I_{S} \omega_{z} \nonumber$$

Para la rotación de eje fijo, nuestro resultado es que el par alrededor de un punto es igual a la derivada de tiempo del momento angular alrededor de ese punto,

$$\vec{\tau}_{S}^{\mathrm{ext}}=\frac{d}{d t} \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}} \nonumber$$

ahora se puede resolver en la dirección z,

$$\tau_{S, z}^{\mathrm{ext}}=\frac{d L_{S, z}^{\mathrm{sys}}}{d t}=\frac{d}{d t}\left(I_{S} \omega_{z}\right)=I_{S} \frac{d \omega_{z}}{d t}=I_{S} \frac{d^{2} \theta}{d t^{2}}=I_{S} \alpha_{z} \nonumber$$

de acuerdo con nuestro resultado anterior de que el componente z del par alrededor del punto$S$ es igual al producto del momento de inercia aproximadamente$I_{S}$ y el componente z de la aceleración angular,$\alpha_{z}$.

Ejemplo 19.6 Anillo circular

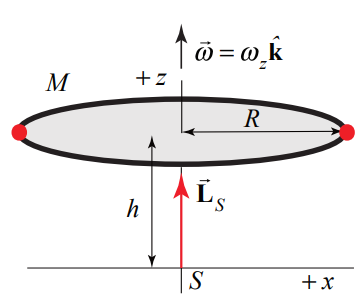
Un anillo circular de radio R y masa M gira alrededor del eje z en un plano paralelo pero a una distancia h por encima del plano x-y. El componente z de la velocidad angular es$\omega_{z}$ (Figura 19.17). Encuentre la magnitud y la dirección del momento angular a$\overrightarrow{\mathbf{L}}_{S}$ lo largo$S$ en cualquier punto del eje z central.

Figura 19.17 Ejemplo 19.6

Solución: Utilice el mismo argumento de simetría que hicimos en el Ejemplo 19.5. El anillo puede pensarse como compuesto por pares de objetos puntiformes en lados opuestos del anillo cada uno de masa m (Figura 19.18).

Figura 19.18 Anillo como suma de pares de partículas distribuidas simétricamente

Cada par tiene un componente z distinto de cero del momento angular tomado alrededor de cualquier punto$S$ a lo largo del eje z,$\overrightarrow{\mathbf{L}}_{S}^{\text {pair }}=\overrightarrow{\mathbf{L}}_{S, 1}+\overrightarrow{\mathbf{L}}_{S, 2}=2 m R^{2} \omega_{z} \hat{\mathbf{k}}=m^{p a i r} R^{2} \omega_{z} \hat{\mathbf{k}}$. El momento angular del anillo alrededor del punto$S$ es entonces la suma sobre todos los pares

$$\overrightarrow{\mathbf{L}}_{S}=\sum_{p a i s} m^{p a i r} R^{2} \omega_{z} \hat{\mathbf{k}}=M R^{2} \omega_{z} \hat{\mathbf{k}} \nonumber$$

Recordemos que el momento de inercia de un anillo viene dado por

$$I_{S}=\int_{\text {body }} d m\left(r_{d m}\right)^{2}=M R^{2} \nonumber$$

Para el anillo simétrico, el momento angular alrededor de$S$ los puntos en la dirección de la velocidad angular y es igual a

$$\overrightarrow{\mathbf{L}}_{S}=I_{S} \omega_{z} \hat{\mathbf{k}} \nonumber$$