17.10: Agua

El agua consiste en una masa$M$ (“oxígeno”) conectada a dos masas iguales menores$m$ (“hidrógeno”) por dos resortes iguales de constantes de fuerza$k$, siendo el ángulo entre los resortes$2\theta$. La longitud de equilibrio de cada resorte es$r$. El par necesario para aumentar el ángulo entre los resortes por$2\delta \theta$ es$2c\delta \theta$. Ver Figura XVII.10. ($\theta$es de aproximadamente 52°.)

En cualquier momento, deje que las coordenadas de las tres masas (de izquierda a derecha) sean

$(x_1,y_1), \qquad (x_2,y_2), \qquad (x_3,y_3)$

y dejar que las posiciones de equilibrio sean

$(x_{10},y_{10}), \qquad (x_{20},y_{20}), \qquad (x_{30},y_{30}), \text{ where} y_{30} = y_{10}$

Suponemos que estas coordenadas se refieren a un marco en el que el centro de masa del sistema es estacionario.

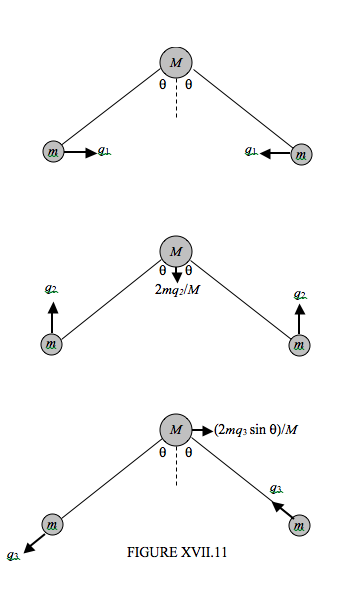
Intentemos imaginar, en la Figura XVII.11, los modos vibracionales. Podemos imaginar fácilmente un modo en el que el ángulo se abre y se cierra simétricamente. Vamos a resolver este modo en un$x$ -componente y un$y$ -componente. En el$x$ -componente de este movimiento, un átomo de hidrógeno se mueve hacia la derecha por una distancia$q_1$ mientras que el otro se mueve hacia la izquierda por e igual distancia$q_1$. En el$y$ -componente de este movimiento simétrico, ambos hidrógenos se mueven hacia arriba una distancia$q_2$, mientras que, para mantener el centro de masa del sistema inmóvil, el oxígeno necesariamente se mueve hacia abajo una distancia$2mq_2/M$. También podemos imaginar un modo asimétrico en el que un resorte se expande mientras que el otro se contrae. Un hidrógeno se mueve hacia abajo a la izquierda por una distancia$q_3$, mientras que el otro se mueve hacia arriba a la izquierda por la misma distancia. Mientras tanto, el oxígeno debe moverse a la derecha por una distancia$(2mq_3 \sin \theta )/M$, para mantener el centro de masa inmóvil.

Vamos a tratar de anotar las energías cinéticas y potenciales en términos de las coordenadas internas$q_1, q_2$ y$q_3$.

Es fácil anotar la energía cinética en términos de las$(x , y)$ coordenadas:

$$T\ =\ \frac{1}{2}m(\dot{x}_{1}^{2}\ +\ \dot{y}_{1}^{2})\ +\ \frac{1}{2}M(\dot{x}_{2}^{2}\ +\ \dot{y}_{2}^{2})\ +\frac{1}{2}m(\dot{x}_{3}^{2}\ +\ \dot{y}_{3}^{2}). \label{17.10.1}$$

Desde la geometría tenemos:

$$\begin{align} \dot{x}_{1} &=\ \dot{q}_{1}-\dot{q}_{3}\sin\theta \\[5pt] \dot{y}_{1} &= \dot{q}_{2}-\dot{q}_{3}\cos\theta \label{17.10.2a,b} \\[5pt] \dot{x}_{2} &= \frac{2m\dot{q}_{3}\sin\theta}{M} \\[5pt] \dot{y}_{2} &= -\frac{2m\dot{q}_{2}}{M} \label{17.10.3a,b} \\[5pt] \dot{x}_{3} &= -\dot{q}_{1} - \dot{q}_{3}\sin\theta \\[5pt] \dot{y}_{3} &= \dot{q}_{2}\ +\ \dot{q}_{3}\cos\theta \label{17.10.4a,b} \end{align}$$

Al poner estos en la ecuación$\ref{17.10.1}$ obtenemos

$$T\ =\ m\dot{q}_{1}^{2}\ +\ m\left(1+\frac{2m}{M}\right)\dot{q}_{2}^{2}\ +\ m\left(1+\frac{(2m\sin^{2}\theta)}{M}\right)\dot{q}_{3}^{2} \label{17.10.5}$$

Para abreviar, voy a escribir esto como

$$T=a_{11}\dot{q}_{1}^{2}+a_{22}\dot{q}_{2}^{2}+a_{33}\dot{q}_{3}^{2} \label{17.10.6}$$

Ahora por la energía potencial.

La extensión del resorte izquierdo es

$$\delta r_{1}=-q_{1}\sin\theta-q_{2}\cos\theta-\frac{2mq_{2}\cos\theta}{M}+q_{3}+\frac{2mq_{3}\sin\theta\cos\theta}{M}\\=-q_{1}\sin\theta-q_{2}\left(\frac{1+2m}{M}\right)\cos\theta+q_{3}\left(1+\frac{(2m\sin^{2}\theta)}{M }\right) \label{17.10.7}$$

La extensión del resorte derecho es

$$\delta r_{2}=-q_{1}\sin\theta-q_{2}\cos\theta-\frac{2mq_{2}\cos\theta}{M}-q_{3}-\frac{2mq_{3}\sin^{2}\theta}{M}\\=-q_{1}\sin\theta-q_{2}\left(\frac{1+2m}{M}\right)\cos\theta-q_{3}\left(1+\frac{(2m\sin^{2}\theta)}{M }\right). \label{17.10.8}$$

El aumento en el ángulo entre los resortes es

$$2\delta\theta=-\frac{2q_{1}\cos\theta}{r}\ +\ \frac{2(1+\frac{2m}{M})q_{2}\sin\theta}{r}. \label{17.10.9}$$

La energía potencial (por encima de la posición de equilibrio) es

$$V=\frac{1}{2}k(\delta r_{1})^{2}\ +\ \frac{1}{2}k(\delta r_{2})^{2}\ +\ \frac{1}{2}c(2\delta\theta)^{2}. \label{17.10.10}$$

Al sustituir Ecuaciones$\ref{17.10.7}$,$\ref{17.10.8}$ y$\ref{17.10.9}$ en esto, obtenemos una ecuación de la forma

$$V=b_{11}q_{1}^{2}\ +\ 2bq_{12}q_{1}q_{2}\ +\ b_{22}q_{2}^{2}\ +\ b_{33}q_{3}^{2}, \label{17.10.11}$$

donde le dejo al lector, si lo desea, que elabore las expresiones detalladas para los coeficientes. Todavía tenemos un término cruzado, así que no podemos separar completamente las coordenadas, pero podemos aplicar fácilmente la ecuación de Lagrange a las Ecuaciones\ ref {17.10.6} y\ ref {17.10.11}, y luego buscar soluciones armónicas simples de la manera habitual. Establecer el determinante de los coeficientes en cero conduce a la siguiente ecuación para las frecuencias angulares de los modos normales:

$$\begin{bmatrix}b_{11}-\omega^{2}a_{11} & b_{12} & 0 \\ b_{12} & b_{22}-\omega^{2}a_{22} & 0\\ 0 & 0 & b_{33}-\omega^{2}a_{33} \end{bmatrix}\ =\ 0. \label{17.10.12}$$

Así, dadas las masas y$r, \theta, k$ y$c$, se pueden predecir las frecuencias de los modos normales. ¿Se puede calcular$k$ y$c$ dadas las frecuencias? No sé, a decir verdad. ¿Puedo dejar que el lector investigue más a fondo?