22.8: Apéndice B

Soluciones a problemas diversos

Ejercicio$\PageIndex{1}$

Por proporciones,$\frac{h}{k}=\frac{n}{x}$ y$\frac{h}{l}=\frac{m}{x}$ y por lo tanto$\frac{h}{k}+\frac{h}{l}=1$.

Por lo tanto por Pitágoras:

$h\left(\frac{1}{\sqrt{a^{2}-x^{2}}}+\frac{1}{\sqrt{b^{2}-x^{2}}}\right)=1.$.

Todo menos$x$ se sabe en esta ecuación, que por lo tanto se puede resolver para$x$. Hay varias formas de resolverlo; aquí hay una sugerencia. Si ponemos en los números, la ecuación se convierte en

$3\left(\frac{1}{\sqrt{64-x^{2}}}+\frac{1}{\sqrt{100-x^{2}}}\right)-1=0.$

Poner$X= 100-x^{2}$, y la ecuación se convierte

$3\left(\frac{1}{\sqrt{X-36}}+\frac{1}{\sqrt{X}}\right)-1=0.$

Esto se puede escribir$f(X)=3(A+B)-1=0$, donde$A$ y$B$ son funciones obvias de$X$. Diferenciación con respecto a$X$ da$f'(X)=-\frac{3}{2}(A^{3}+B^{3})$ y la iteración de Newton-Raphson$(X=X-\frac{f}{f'})$ pronto da$X$, de la que luego se encuentra que$x$ = 6.326 182 m.

Ejercicio$\PageIndex{2}$

En el marco corrotativo el bob está en equilibrio bajo la acción de tres fuerzas: su peso, la tensión en la cuerda y la fuerza centrífuga. (Si no te gustan los marcos de referencia giratorios y la fuerza centrífuga, te será fácil hacerlo “correctamente”). Resolver las fuerzas perpendiculares a la cuerda:$ml_{0}\sin\alpha\Omega^{2}.\cos\alpha\ =\ mg\sin\alpha$ y el problema está terminado.

Ejercicio$\PageIndex{3a}$

Al subir o bajar el tablero no se aplican pares de torsión al sistema, por lo que$L$ se conserva el momento angular. Es decir,

$$L=ml^{2}\sin^{2}\theta.\omega \qquad \text{is constant.} \tag{1}\label{1}$$

También tenemos eso

$$\text{g}\ =\ l\cos\theta.\omega. \tag{2}\label{2}$$

i. Eliminar w de estas ecuaciones. Esto da:

$$l^{3}\sin^{3}\theta\tan\theta=\frac{L^{2}}{\text{g}m^{2}} \tag{3}\label{3}$$

que es constante.

ii. Eliminar$l$ de las ecuaciones ($\ref{1}$) y ($\ref{2}$). Esto da:

$$\omega^{3}\cot^{2}\theta=\frac{m\text{g}^{2}}{L}, \tag{4}\label{4}$$

que es constante.

iii. Eliminar$\theta$ de las ecuaciones ($\ref{1}$) y ($\ref{2}$). Esto da:

$$\omega^{3}\left(\omega l^{2}-\frac{L}{m}\right)=\text{g}^{2}. \tag{5}\label{5}$$

(Verifique las dimensiones de todas las ecuaciones.) Entonces podemos obtener$\frac{L}{m}$ de equation ($\ref{1}$) y por lo tanto

$\omega^{3}(\omega l^{2}-\Omega l_{0}^{2}\sin^{2}\alpha)=\text{g}^{2}$,

que es constante.

Ejercicio$\PageIndex{3b}$

i.

$l^{3}\sin^{3}\theta\tan\theta=l_{0}^{3}\sin^{3}\alpha\tan\alpha=0.023675\ \text{m}^{3}.$

Aunque se nos pide que trazar$\theta$ verticalmente versus$l$ horizontalmente, es más fácil, al elaborar valores numéricos, calcular$l$ en función de$\theta$. Es decir,

$l\ =\ \frac{0.287142}{\sin\theta\sqrt[3]{\tan\theta}}$.

(El número en el numerador es la raíz cubo de 0.023675.)

Para$l$ = 40 cm = 0.4 m, el ángulo semivertical viene dado por

$\sin^{3}\theta\tan\theta=0.369\ 923$.

La solución a esto es

$\theta=45^{\circ}\ 31'$.

(Consulte la Sección 1.4 de Mecánica Celestial si necesita saber cómo resolver la ecuación)$f(x)=0$.

ii.

$\omega^{3}\cot^{2}\theta=\Omega^{3}\cot^{2}\alpha$

Con los datos dados, esto es$\omega^{3}=199.385\tan^{2}\theta$.

iii. $\omega^{3}(\omega l^{2}-\Omega l_{0}^{2}\sin^{2}\alpha)=\ \Omega^{3}(\Omega l_{0}^{2}\ -\ \Omega l_{0}^{2}\sin^{2}\alpha)=\Omega^{4}l_{0}^{2}\cos^{2}\alpha$.

Es decir,$\omega^{3}(\omega l^{2}\ -a)=\ \text{g}^{2}$ donde, con los datos iniciales dados,

$a=0.48168\ \text{m}^{2}\text{s}^{-1}$y$\text{g}^{2}\ =\ 96.04\ \text{m}^{2}\text{s}^{-4}$.

Aunque se nos pide que trazar$\omega$ verticalmente versus$l$ horizontalmente, es más fácil, al elaborar valores numéricos, calcular l en función de$\omega$. Es decir,

$l^{2}\ =\ \frac{\text{g}^{2}}{\omega^{4}}+\frac{a}{\omega}$.

Resolver la ecuación anterior para$\omega$ podría ser un poco más fácil con la sustitución de$u$ for$\frac{1}{\omega}$:

$\text{g}^{2}u^{4}\ +\ au\ -l^{2}=0$.

Con $l$= 0.6 m, esto da$u$ = 0.226121 rad ^{- 1} s, y por lo tanto$\omega$ = 4.422 rad s ^{- 1}. Al igual que en la parte b) i, es necesario saber resolver la ecuación$f(x)=0$. Consulta la Sección 1.4 de Mecánica Celestial si necesitas saber cómo.

Ejercicio$\PageIndex{4}$

No hay fuerzas horizontales, porque la mesa es lisa. Por lo tanto, el centro de masa de la varilla cae verticalmente.centro de masa de la varilla cae verticalmente.

A partir de consideraciones energéticas

$$\frac{1}{2}m\dot{y}^{2}\ +\ \frac{1}{2}\left(\frac{1}{3}ml^{2}\right)\dot{\theta}^{2}\ +\ mgy\ = \text{constant}. \tag{1}\label{4.1}$$

Pero$y\ =\ l\cos\theta$ y por lo tanto$\dot{y}=-l\sin\theta.\dot{\theta}$.

$$(3\sin^{2}\theta\ +\ 1)l\dot{\theta}^{2}\ +\ 6\text{g}\sin\theta=C. \tag{2}\label{4.2}$$

Inicialmente$\theta=\dot{\theta}=0, \quad \therefore C=6\text{g}$.

$$\underline{\underline{\dot{\theta}^{2}\ =\ \frac{6\text{g}(1-\cos\theta)}{l(3\sin^{2}\theta+1)}}} \tag{3}\label{4.3}$$

Además, desde$\dot{y}^{2}=l^{2}\sin^{2}\theta\dot{\theta}^{2}$ y$\dot{x}^{2}=l^{2}\cos^{2}\theta\dot{\theta}^{2}$, obtenemos

$$\underline{\underline{\dot{y}^{2}\ =\ \frac{6\text{g}l\sin^{2}\theta(1-\cos\theta)}{3\sin^{2}\theta+1}}} \tag{4}\label{4.4}$$

y

$$\underline{\underline{\dot{x}^{2}\ =\ \frac{6\text{g}l\cos^{2}\theta(1-\cos\theta)}{3\sin^{2}\theta+1}}} \tag{5}\label{4.5}$$

Por supuesto$\dot{\theta}$ y$\dot{y}$ aumentar monótonamente con$\theta$; pero$\dot{x}$ inicia y termina en cero, y debe pasar por un máximo. Con$c\ =\ \cos\theta$, la ecuación ($\ref{5}$) se puede escribir

$$\dot{x}^{2}\ =\ \frac{6\text{g}lc(1-c)}{4-3c^{2}}, \tag{6}\label{4.6}$$

y diferenciando$\dot{x}^{2}$ con respecto a$c$, vemos que$\dot{x}^{2}$ es mayor en un ángulo$\theta$ dado por

$$3c^{2}\ -12c+8=0, \tag{7}\label{7}$$

cuya solución es$\underline{\underline{\theta\ =\ 37^{\circ}\ 50'}}$.

Si la longitud de la varilla es de 1 m ($l$= 0.5 m) y$\dot{x}$ = 1 m s ^{- 1}, la Ecuación$\ref{4}$ se convierte

$$26.4c^{2}\ -29.4c\ +\ 4\ =\ 0, \tag{8}\label{8}$$

y las dos soluciones son$\underline{\underline{\theta\ =\ 17^{\circ}\ 15'}}$ y$\underline{\underline{80^{\circ}\ 52'}}$.

El lector que ha hecho todos los problemas hasta el momento será consciente de la importancia de poder resolver instantáneamente la ecuación$f(x)=0$. Si aún no lo has hecho, debes escribir un programa de computadora o calculadora que te permita hacerlo al instante y en cualquier momento. Consulta la Sección 1.4 de Mecánica Celestial si necesitas saber cómo.

Si quieres encontrar la reacción normal$N$ de la mesa en el extremo inferior de la varilla, tal vez podrías comenzar con la ecuación vertical del movimiento$m\ddot{y}=N-mg$. Diferenciar Ecuación ($\ref{4}$):$2\dot{y}\ddot{y}=$ lo que sea, y la ecuación de uso

$\ref{4}$otra vez para$\dot{y}$. Esto me parece un álgebra bastante pesada y poco interesante, así que no voy a perseguirla. Puede haber una mejor manera...

Ejercicio$\PageIndex{5}$

En la siguiente figura he marcado en rojo las fuerzas sobre la varilla, es decir, su peso$mg$ y los componentes horizontal y vertical$X$ y$Y$ de la reacción de la bisagra sobre la varilla. También he marcado, en verde, los componentes transversales y radiales de la aceleración del centro de masa. El componente transversal es$l\ddot{\theta}$ y el componente radial es la aceleración centrípeta$l\dot{\theta}^{2}$ .centro de masa. El componente transversal es$l\ddot{\theta}$ y el componente radial es la aceleración centrípeta$l\dot{\theta}^{2}$.

A partir de la consideración del momento de la fuerza$mg$ alrededor del extremo inferior de la varilla, es evidente que la aceleración angular es

$$\ddot{\theta}=\frac{3\text{g}\sin\theta}{4l} \tag{1}\label{5.1}$$

y escribiendo$\ddot{\theta}$ como$\frac{\dot{\theta}d\dot{\theta}}{d\theta}$ e integrando (con condiciones iniciales$\theta\ =\ \dot{\theta}\ =\ 0$), o a partir de consideraciones energéticas, obtenemos la velocidad angular:

$$\dot{\theta}^{2}=\frac{3\text{g}(1-\cos\theta)}{2l}. \tag{2}\label{5.2}$$

Las ecuaciones horizontales y verticales de movimiento son:

$$X=ml(\ddot{\theta}\cos\theta-\dot{\theta}^{2}\sin\theta) \tag{3}\label{5.3}$$

y

$$mg\ -\ Y\ =\ ml(\ddot{\theta}\sin\theta\ +\ \dot{\theta}^{2}\cos\theta). \tag{4}\label{5.4}$$

(Como siempre, comprueba las dimensiones - ¡y cuenta los puntos!)

Después de la sustitución por$\ddot{\theta}$ y$\dot{\theta}^{2}$ encontramos

$$X\ =\ \frac{3}{4}m\text{g}\sin\theta(3\sin\theta-2) \tag{5}\label{5.5}$$

y

$$Y\ =\ \frac{1}{4}m\text{g}(1-3\cos\theta)^{2}. \tag{6}\label{5.6}$$

Los resultados siguen de inmediato.

Ejercicio$\PageIndex{6}$

Llama a la longitud de la varilla$2l$. Inicialmente la altura por encima de la tabla de su centro de masa es$l \cos 40$ °, y su energía potencial gravitacional lo es$m\text{g}\ l\ \cos40^{\circ}$. Cuando golpea la mesa a velocidad angular w, su energía cinética es$\frac{1}{2}I\omega^{2}\ =\ \frac{1}{2}\left(\frac{4}{3}ml^{2}\right)\omega^{2}\ =\ \frac{2}{3}ml^{2}\omega^{2}$. Por lo tanto,

$\omega\ =\ \sqrt{\frac{3\text{g}\cos40^{\circ}}{2l}}\ =\ \underline{\underline{4.746\ \text{rad s}^{-1}\ =271.9\ \text{deg s}^{-1}}}$.

Para encontrar el tiempo tomado, puedes usar la Ecuación 9.2.10:

$$t\ =\ \sqrt{\frac{I}{2}}\int_{40^{\circ}}^{90^{\circ}}\frac{d\theta}{\sqrt{E-V(\theta)}}. \tag{7}\label{6.7}$$

Aquí,$I\ =\ \frac{3}{4}ml^{2},\ E=m\text{g}l\cos40^{\circ},\ V(\theta)\ =\ m\text{g}l\cos\theta$ y por lo tanto

$$t\ =\ \sqrt{\frac{2l}{3\text{g}}}\int_{40}^{90}\frac{d\theta}{\sqrt{\cos40^{\circ}-\cos\theta}}. \tag{8}\label{6.8}$$

La magnitud de la cantidad antes del signo integral es de 0.184428 s. Para encontrar el valor de la integral se requiere o bien que seas un experto en integrales elípticas o (más probable y más útil) que sepas integrar numéricamente (ver Mecánica Celestial 1.2.) Hago el valor de la integral 2.187314, de modo que el tiempo tomado es de 0.4034 segundos. Al integrar, tenga en cuenta que el valor del integrando es infinito en el límite inferior. Cómo lidiar con esta dificultad se trata en Mecánica Celestial 1.2. No se puede pasar por alto.

Ejercicio$\PageIndex{7}$

Aquí está el diagrama. Las fuerzas son el peso$m\text{g}$ de la varilla, y la fuerza de la mesa sobre la varilla. Sin embargo, he resuelto este último en dos componentes: la reacción normal$N$ de la mesa sobre la varilla, y la fuerza de fricción$F$, que puede ser ya sea hacia la izquierda o hacia la derecha, dependiendo de si la varilla tiende a deslizarse hacia la derecha o hacia la izquierda. La magnitud de$F$ es menor que$\mu N$ siempre y cuando la varilla no se jus sobre el deslizamiento. Cuando la varilla está a punto de deslizarse,$F=\mu N,\ \mu$ siendo el coeficiente de fricción estática limitante.

Al igual que en el Problema 5, las ecuaciones de movimiento, siempre y cuando la varilla no se deslice, son

$$F\ =\ \frac{3}{4}m\text{g}\sin\theta(3\cos\theta-2) \tag{1}\label{7.1}$$

y

$$N\ =\ \frac{1}{4}m\text{g}(1-3\cos\theta)^{2}. \tag{2}\label{7.2}$$

$$\frac{F}{N}=\frac{3\sin\theta(3\cos\theta-2)}{(1-3\cos\theta)^{2}}. \tag{3}\label{7.3}$$

La siguiente figura muestra$\frac{F}{N}$ como una función de$\theta$. Se ve que, a medida que la varilla cae,$\frac{F}{N}$ aumenta y, en cuanto alcanza un valor de$\mu$, la varilla se deslizará. Vemos, sin embargo, que$\frac{F}{N}$ alcanza un valor máximo, y por cálculo podemos determinar que alcanza un valor máximo de$\frac{15\sqrt{10}}{128}\ =\ 0.3706$ cuándo$\theta\ =\ \theta^{-1}\left(\frac{9}{11}\right)=35^{\circ}06'$. Si$\mu$ < 0.3706, la parte inferior de la varilla se deslizará antes$\theta=35^{\circ}06'$. Si, sin embargo,$\mu$ > 0.3706, la varilla no se habrá deslizado en el momento$\theta=35^{\circ}06'$, y es segura por un tiempo ya que$\frac{F}{N}$ comienza a disminuir. Cuando$\theta$ alcanza$\cos^{-1}\left(\frac{2}{3}\right)=48^{\circ}11'$, la fuerza de fricción cambia de signo y posteriormente actúa hacia la izquierda. (La fuerza de fricción de la mesa sobre la varilla actúa hacia la izquierda; la fuerza de fricción de la varilla sobre la mesa actúa hacia la derecha). Ya sabemos (ya que la varilla sobrevivió deslizándose antes de$\theta=35^{\circ}06'$ que la magnitud de$\frac{F}{N}$ puede ser al menos tan grande

como 0.3706, y no llega a esto hasta$\theta=51^{\circ}15'$. Por lo tanto, si la varilla no se ha deslizado por$\theta=51^{\circ}15'$ ella no se deslizará antes$\theta=51^{\circ}15'$. Pero después de eso vuelve a estar en peligro de resbalar. $\frac{F}{N}$se convierte en infinito ($N=0$) cuando$\theta=\cos^{-1}\left(\frac{1}{3}\right)=70^{\circ}32'$, por lo que sin duda se deslizará (hacia la derecha) antes de entonces.

Si$\mu=0.25$, la varilla se deslizará hacia la izquierda cuando

$\frac{3\sin\theta(3\cos\theta-2)}{(1-3\cos\theta)^{2}}\ =\ \frac{1}{4},\ \text{or}\ \underline{\underline{\theta=19^{\circ}39'}}$.

Si$\mu = 0.75$, la varilla se deslizará hacia la derecha cuando

$\frac{3\sin\theta(3\cos\theta-2)}{(1-3\cos\theta)^{2}}\ =\ -\frac{3}{4},\ \text{or}\ \underline{\underline{\theta=53^{\circ}07'}}$.

Nuevamente, es muy necesario que prepares para ti mismo un programa que resuelva instantáneamente la ecuación$f(x)=0$.

Ejercicio$\PageIndex{8}$

Deja que la longitud de la escalera sea$2l$. Por geometría, la distancia OC permanece igual a$l$ lo largo del movimiento; por lo tanto C describe un círculo de radio$l$, centro O. He marcado en, en verde, los componentes radial y transversal de la aceleración de C, es decir,$l\dot{\theta}^{2}$ y$l\ddot{\theta}$. La velocidad angular de la escalera es$\dot{\theta}$ y la velocidad lineal del centro de masa C es$l\ddot{\theta}$. También he marcado, en rojo, las tres fuerzas que actúan sobre la escalera, es decir, su peso y las reacciones del piso y la pared en la escalera.centro O. He marcado en, en verde, los componentes radial y transversal de la aceleración de C, es decir$l\dot{\theta}^{2}$ y$l\ddot{\theta}$. La velocidad angular de la escalera es$\dot{\theta}$ y la velocidad lineal del centro de masa C es$l\ddot{\theta}$. También he marcado, en rojo, las tres fuerzas que actúan sobre la escalera, es decir, su peso y las reacciones del piso y la pared de la escalera.

La velocidad angular se$\dot{\theta}$ puede obtener a partir de consideraciones energéticas. Es decir, la pérdida de energía potencial al pasar del ángulo a al vertical al ángulo$\theta$ es igual a la ganancia en las energías cinéticas de traslación y rotación:

$m\text{g}l(\cos\alpha-\cos\theta)=\frac{1}{2}m(l\dot{\theta})^{2}\ +\ \frac{1}{2}\left(\frac{1}{2}ml^{2}\right)\dot{\theta}^{2}$.

$$\dot{\theta}^{2}=\frac{3\text{g}}{2l}(\cos\alpha-\cos\theta). \tag{1}\label{8.1}$$

La aceleración angular se$\ddot{\theta}$ puede obtener a partir de la siguiente ecuación:

$$m\text{g}l\sin\theta=\frac{4}{3}ml^{2}\ddot{\theta} \tag{2}\label{8.2}$$

La derivación de la Ecuación ($\ref{2}$) plantea algunos puntos de interés, y lo discuto en un Apéndice al final del problema.

Las ecuaciones verticales y horizontales de movimiento son:

$$N_{2}\ =\ m(l\ddot{\theta}\cos\theta-l\dot{\theta}^{2}\sin\theta) \tag{3}\label{8.3}$$

y

$$m\text{g}\ -\ N_{1}\ =m(l\ddot{\theta}\sin\theta\ +\ l\dot{\theta}\cos\theta), \tag{4}\label{8.4}$$

aunque sólo necesitamos el primero de ellos, porque deseamos saber cuándo$N_{2}\ =\ 0$.

En sustitución de$\ddot{\theta}$ y$\dot{\theta}^{2}$ encontramos que

$$N_{2}\ =\ \frac{3}{4}m\text{g}\sin\theta(3\cos\theta-2\cos\alpha) \tag{5}\label{8.5}$$

y

$$N_{1}\ =\ \frac{1}{4}m\text{g}(1-6\cos\alpha\cos\theta+9\cos^{2}\theta) \tag{6}\label{8.6}$$

Solo necesitamos el primero de estos para ver que$N_{2}$ se convierte en cero (y de ahí que el extremo superior pierda contacto con la pared) cuando$\cos\theta=\frac{2}{3}\cos\alpha$.

Apéndice: Derivación de la ecuación (2).

En mi publicación original de esta solución había derivado Equation ($\ref{2}$) considerando que el momento total de todas las fuerzas sobre$Q$ es$m\text{g}l\sin\theta$, y la inercia rotacional con respecto a$Q$ es$\frac{4}{3}ml^{2}$. Entonces equiparé$m\text{g}l\sin\theta$ a$\frac{4}{3}ml^{2}\ddot{\theta}$. Estoy en deuda con el corresponsal Amin Rezaee Zadeh por señalar una falla en este argumento, y por suministrar una derivación correcta. El defecto es que estoy aplicando la ecuación$\bf{\tau=\dot{L}}$ a un punto móvil$Q$. En la Sección 3.12 del Capítulo 3 de estas notas se señala que$\bf{\tau=\dot{L}}$ puede aplicarse a un punto móvil sólo si el punto móvil satisface una o más de tres condiciones, y es evidente en este problema que no$Q$ satisface ninguna de estas condiciones. Presento a continuación la correcta derivación del señor Rezaee de la Ecuación ($\ref{7.2}$).

Estaré haciendo uso de Ecuaciones$\ref{3.12.1}$ y$\ref{3.12.2}$:

$$\dot{L}_{Q}\ =\ \tau_{Q}\ +\ Mr'_{q}\ \times\ \ddot{r}_{Q}. \tag{3.12.1}\label{3.12.1}$$

$$L_{Q}\ =\ \Sigma(r_{i}-r_{Q})\times[m_{i}(v_{i}-v_{Q})]. \tag{3.12.2}\label{3.12.2}$$

También estaré haciendo uso de la notación utilizada en la Sección 3.12, y reproduzco aquí la Figura III.7 de esa Sección, y también dibujo los vectores pertinentes apropiados a este problema de escalera.

En la siguiente figura, he indicado una porción elemental$ds$ de la escalera a una$s$ distancia del extremo superior de la escalera. Su masa es evidentemente$dm=\frac{mds}{2l}$. He dibujado los vectores de posición$\bf{r}_{i}$ y$\bf{r}_{O}$ de$ds$ y de$Q$. Esta notación corresponde a la misma notación utilizada en la Sección 3.12. A partir de la geometría de la figura, podemos determinar que

$$\textbf{r}_{i}\ =\ s\sin\theta\textbf{i}\ +\ (2l-s)\cos\theta\textbf{j} \tag{A1}\label{A1}$$

y

$$\textbf{r}_{Q}\ =\ 2l\sin\theta\textbf{i}\ +\ 2l\cos\theta\textbf{j}, \tag{A2}\label{A2}$$

donde$\textbf{i}$ y$\textbf{j}$ son los vectores unitarios en las$y-$ direcciones$x-$ y respectivamente.

Sobre la diferenciación con respecto al tiempo, encontramos las siguientes expresiones para las velocidades del elemento$ds$ y el punto$Q$, en las que nuevamente retengo la notación utilizada en la Sección 3.12:

$$\textbf{v}_{i}\ =\ s\dot{\theta}\cos\theta\textbf{i}\ -\ (2l-s)\dot{\theta}\sin\theta\textbf{j} \label{A3}\tag{A3}$$

y

$$\textbf{v}_{Q}\ =\ 2l\dot{\theta}\cos\theta\textbf{i}\ -\ 2l\dot{\theta}\sin\theta\textbf{j} \label{A4}\tag{A4}$$

Al hacer uso de la Ecuación$\ref{3.12.2}$, obtenemos para el momento angular del elemento$ds$ con respecto a$Q$:

$$d\textbf{L}_{Q}\ =\ \frac{m}{2l}(\textbf{r}_{i}-\textbf{r}_{Q})\times[(\textbf{v}_{i}-\textbf{v}_{Q})]ds. \tag{A5}\label{A5}$$

Por lo tanto, el momento angular instantáneo de toda la escalera$Q$ es

$$\textbf{L}_{Q}\ =\ \frac{m}{2l}\int_{0}^{2l}(\textbf{r}_{i}-\textbf{r}_{Q})\times[(\textbf{v}_{i}-\textbf{v}_{Q})]ds. \tag{A6}\label{A6}$$

Al sustituir las ecuaciones ($\ref{A1}$) — ($\ref{A4}$) en la ecuación ($\ref{A6}$) y una modesta cantidad de álgebra, obtenemos

$$\textbf{L}_{Q}\ =\ \frac{m\theta\textbf{k}}{2l}\int_{0}^{2l}s(s-2l)ds\ =\ -\frac{2}{3}ml^{2}\dot{\theta}\textbf{k}, \label{A7}\tag{A7}$$

donde$\textbf{k}$ está el vector unitario en la$z-$ dirección. (La$z-$ dirección está fuera del plano del “papel”, y por lo tanto$\bf{L}_{Q}$ está en el plano del “papel”. Vale la pena pasar uno o dos momentos tratando de imaginarlo. La escalera gira en sentido antihorario alrededor de C, mientras que C y Q se mueven en trayectorias en sentido horario. Puede que no sea inmediatamente obvio decidir si uno esperaría$\bf{L}_{Q}$ ser dirigido dentro o fuera del plano del “papel”. La ecuación ($\ref{A7}$) responde a esta pregunta.)

Ahora hacemos uso de la ecuación$\ref{3.12.1}$:

$$\dot{\bf{L}}_{Q}\ =\ \tau_{Q}\ +\ m\bf{r'}_{Q}\times\bf{\ddot{r}}_{Q}. \tag{A8}\label{A8}$$

Busquemos expresiones para las cuatro cantidades vectoriales en esta ecuación.

Por diferenciación de la Ecuación ($\ref{A7}$) con respecto al tiempo, obtenemos

$$\dot{\bf{L}}_{Q}\ =\ -\frac{2}{3}ml^{2}\ddot{\theta}\textbf{k}. \tag{A9}\label{A9}$$

El par sobre Q es

$$\tau_{Q}\ =\ mgl\sin\theta\textbf{k} \tag{A10}\label{A10}$$

Podemos ver a partir de la geometría de la figura (ver especialmente la segunda de nuestras figuras, en la que vemos eso$\textbf{r}'_{Q}$ y$\overline{\textbf{r}}$ son lo mismo en magnitud y dirección) que

$$\textbf{r}^{\prime}_{Q}\ =\ l\sin\theta\textbf{i}\ +\ l\cos\theta\textbf{j}. \tag{A11}\label{A11}$$

Finalmente, por diferenciación de la Ecuación ($\ref{A4}$) (en la cual), obtenemos

$$\ddot{\textbf{r}}_{Q}\ =\ 2l[(\ddot{\theta}\cos\theta-\dot{\theta}^{2}\sin\theta)\textbf{i}\ -\ (\ddot{\theta}\sin\theta-\dot{\theta}^{2}\cos\theta)\textbf{j}]. \tag{A12}\label{A12}$$

La sustitución de las ecuaciones ($\ref{A9}$) a ($\ref{A12}$) en la ecuación ($\ref{A8}$) da, después de algún álgebra,

$$mgl\sin\theta\ =\ \frac{4}{3}ml^{2}\ddot{\theta}. \tag{A13}\label{A13}$$

Esta es la ecuación ($\ref{2}$), quod erat demonstrandum.

Ejercicio$\PageIndex{9}$

Creo que se acordará que el punto O permanezca fijo en el espacio mientras el semicilinder permanezca en contacto con pared y piso. Por lo tanto, el centro de masa C se mueve en círculo alrededor de O. Llamaremos al radio del círculo, que es la distancia entre O y C$b$, que, para un semicilínder, equivale al centro de masa C se mueve en un círculo alrededor de O. Llamaremos al radio del círculo, que es la distancia entre O y C, $b$, que, para un semicilinder, es igual$\frac{4a}{(3\pi)}$ (ver Capítulo 1), donde$a$ está el radio del semicilinder. He marcado, en rojo, las tres fuerzas en el semicilinder, y también, en verde, los componentes radial y transversal de la aceleración.

La velocidad angular se$\dot{\theta}$ puede obtener a partir de consideraciones energéticas. La ganancia en energía cinética al pasar del reposo a una velocidad angular$\dot{\theta}$ es$\frac{1}{2}\left(mk^{2}\right)\dot{\theta}^{2}$ y la ganancia en energía potencial cuando el centro de masa cae a través de una distancia vertical$b\ \sin\theta$ es$mgb\sin\theta$. Aquí$k$ está el radio de giro alrededor de O, que, para un semicilinder, viene dado por$k^2 = \frac{1}{2}a^2$.

[Me queda$b$ and $k$ as they are in the equations, so that the analysis could easily be adapted, if needed, for a hollow semicylinder, or a solid hemisphere, or a hollow hemisphere. From Chapters 1 and 2 we recall:

Semicilinder sólido:	$b=\frac{4a}{3\pi}$	$k^{2}\ =\ \frac{1}{2}a$	$\frac{b^{2}}{k^{2}}\ =\ \frac{32}{9\pi^{2}}$
Semicylinder hueco:	$b=\frac{2a}{\pi}$	$k^{2}\ =\ a^{2}$	$\frac{b^{2}}{k^{2}}\ =\ \frac{4}{\pi^{2}}$
Hemisferio sólido:	$b=\frac{3a}{8}$	$k^{2}\ =\ \frac{2}{5}a^{2}$	$\frac{b^{2}}{k^{2}}\ =\ \frac{45}{128}$
Hemisferio hueco:	$b=\frac{1}{2}a$	$k^{2}\ =\ \frac{2}{3}a^{2}$	$\frac{b^{2}}{k^{2}}\ =\ \frac{3}{8}$

Al equiparar la ganancia de energía cinética con la pérdida de energía potencial, obtenemos

$$\dot{\theta}^{2}\ =\ \frac{2b\text{g}}{k^{2}}\sin\theta. \tag{1}\label{9.1}$$

La aceleración angular se$\ddot{\theta}$ puede obtener aplicando$\tau\ =\ I\ddot{\theta}$ aproximadamente O:

$m\text{g}b\cos\theta\ =\ mk^{2}\ddot{\theta}$,

a partir de la cual

$$\ddot{\theta}\ =\ \frac{bg}{k^{2}}\cos\theta \tag{2}\label{9.2}$$

Las ecuaciones horizontales y verticales de movimiento son

$$N_{2}\ =\ mb(\dot{\theta}^{2}\cos\theta\ + \ddot{\theta}\sin\theta) \tag{3}\label{9.3}$$

y

$$N_{2}\ =\ mb(\dot{\theta}^{2}\cos\theta\ + \ddot{\theta}\sin\theta) \tag{4}\label{9.4}$$

Realmente no necesitamos Equation ($\ref{4}$), porque estamos tratando de determinar cuándo$N_{2}=0$.

Al sustituir las ecuaciones ($\ref{1}$) y ($\ref{2}$), la ecuación ($\ref{3}$) se convierte

$$N_{1}=\frac{6mb^{2}\text{g}}{a^{2}}\sin\theta\cos\theta. \tag{5}\label{9.5}$$

Esto es cero cuando$\theta\ =\ 0^{\circ}$ (cual fue la condición inicial) o cuándo$\theta\ =\ 0^{\circ}$, en cuyo punto se pierde el contacto con la pared, lo que se requería mostrar.

En este instante, la velocidad de rotación es en$\sqrt{\frac{2b\text{g}}{k^{2}}}$ sentido antihorario.

y la velocidad lineal de C es$b\sqrt{\frac{2b\text{g}}{k^{2}}}$ horizontal a la derecha.

La energía cinética rotacional es$\frac{1}{2}I\omega^{2}$ donde$\omega\ =\ \sqrt{\frac{2b\text{g}}{k^{2}}}$, y$I$ es la inercia rotacional alrededor del centro de masacentro de masa, que es$m(k^{2}-b^{2})$.

$K_{\text{rot}}=\frac{mb\text{g}(k^{2}-b^{2})}{k^{2}}$.

La energía cinética traslacional es$\frac{1}{2}mv^{2}$ donde está$v\ =\ \sqrt{\frac{2bg}{k^{2}}}$.

$K_{\text{tr}}\ =\ \frac{mb^{3}\text{g}}{k^{2}}$

La suma de estos es$mb\text{g}$, que es igual a la pérdida de la energía potencial original, que sirve como un control de la exactitud de nuestro álgebra.

Ahora no hay fuerzas horizontales, por lo que la componente horizontal de la velocidad de C permanece constante. El semicilinder continúa girando, sin embargo, hasta que la energía cinética rotacional se convierte en energía potencial y C se eleva a su altura máxima. Si la base hace entonces un ángulo$\phi$ con la vertical, la ganancia en energía potencial es$mb\text{g}\sin\phi$, y equiparando esto a la energía cinética rotacional da

$\sin\phi\ =\ 1\ -\ \frac{b^{2}}{k^{2}}$.

Esto da los siguientes resultados:

Semicilinder sólido:	$\phi\ =\ 39^{\circ}\ 46'$
Semicylinder hueco:	$\phi\ =\ 36^{\circ}\ 30'$
Hemisferio sólido:	$\phi\ =\ 40^{\circ}\ 25'$
Hemisferio hueco:	$\phi\ =\ 38^{\circ}\ 41'$

Ejercicio$\PageIndex{10}$

Agrega texto aquí. Para que el número automático funcione, es necesario agregar la plantilla “AutoNum” (preferiblemente al final) a la página.

Es bien sabido que si$\alpha\ >\ \tan^{-1}\mu$ la partícula se deslizará por el avión a menos que sea ayudada por una fuerza extra. Yo he dibujado las tres fuerzas que actúan sobre la partícula. Su peso$mg$. La reacción$R$ del plano sobre la partícula; si la partícula está en equilibrio estático limitante, esta reacción hará un ángulo$\lambda$ (“el ángulo de fricción”) con el plano tal que$\tan\lambda\ =\ \mu$. Por lo tanto hace un ángulo$\alpha-\theta$ con la vertical. Por último, la fuerza adicional$P$ necesaria; inicialmente desconocemos la dirección de esta fuerza.

Cuando tres (o más) fuerzas coplanarias están en equilibrio y se dibujan de cabeza a cola, forman un triángulo cerrado (polígono). Dibujo el triángulo de fuerzas de abajo.

Quedará claro desde el triángulo que$P$ is least when the angle between $\textbf{P}$ and $\textbf{R}$ is $90^{\circ}$:

The least value of $P$ is therefore $m\text{g}(\sin\alpha\cos\lambda\ -\ \cos\alpha\sin\lambda)$. But $\tan\lambda=\mu$ and therefore $\sin\lambda=\frac{\mu}{\sqrt{1+\mu^{2}}}$ and $\cos\lambda=\frac{1}{\sqrt{1+\mu^{2}}}$.

$P_{\text{min}}=\frac{m\text{g}(\sin\alpha-\mu\cos\alpha)}{\sqrt{1-\mu^{2}}}$

and $P$ then makes an angle \( \lambda\) with the plane.

You may, if you wish, go further, and show that when $\textbf{P}$ makes an angle $\beta$ with the plane, it must have magnitude

$P=\frac{\sin\alpha-\mu\cos\alpha}{\mu\sin\beta\ +\ \cos\beta}m\text{g}$.

You can then differentiate this with respect to $\beta$ (you need only differentiate the denominator) and show that this is a minimum when $\beta\ =\ \lambda$. That is just a harder way of finding what we already found by using the triangle of forces.

For $\alpha\ =\ 70^{\circ}$ and $\mu\ =\ 0.8$, $P$ varies with $\beta$ like this:

This goes through a minimum of $P_{\text{min}}=0.520m\text{g}$ at $\beta\ =\ \tan^{-1}0.8=38^{\circ}.7$.

_________________________

Exercise $\PageIndex{11}$

Add text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.

As the cylinder rolls down the plane, the wedge, because its base is smooth, will slide towards the left. Since there are no external horizontal forces on the system, the centre of mass of the system will not move horizontally (or, rather, it won’t accelerate horizontally.)centre of mass of the system will not move horizontally (or, rather, it won’t accelerate horizontally.)

As usual, we draw a large diagram, using a ruler , and we mark in the forces in red and the accelerations in green, after which we’ll apply $F\ =\ ma$ to the cylinder, or to the wedge, or to the system as a whole, in two directions. It should be easy and straightforward.

I have drawn the linear acceleration $\ddot{s}$ of the cylinder down the slope, and its angular acceleration $\ddot{\theta}$. I have drawn the linear acceleration $\ddot{x}$ of the wedge, which is also shared with the cylinder. I have drawn the gravitational force $mg$ on the cylinder. There is one more force on the cylinder, namely the reaction of the wedge on the cylinder. But I’m not sure in which direction to draw it. Is it normal to the plane? That would mean there is no frictional force between the cylinder and the plane. Is that correct (remembering that both the cylinder and the wedge are accelerating)? Of course I could calculate the moment of the force $mg$ about the point of contact of the cylinder with the plane, and then I wouldn’t need to concern myself with any forces at that point of contact.

But then that point of contact is not fixed. Oh, dear, I’m getting rather muddled and unsure of myself.

This problem, in fact, is ideally suited to a lagrangian rather than a newtonian treatment, and that is what we shall do. Lagrange proudly asserted that it was not necessary to draw any diagrams in mechanics, because it could all be done analytically. We are not quite so talented as Lagrange, however, so we still need a large diagram drawn with a ruler. But, instead of marking in the forces and accelerations in red and green, we mark in the velocities in blue.

No frictional or other nonconservative forces do any work, so we can use Lagrange’s equations of motion for a conservative holonomic system; $\frac{d}{dt}\left(\frac{\partial T}{\partial \dot{q}}\right)-\left(\frac{\partial T}{\partial q}\right)=-\left(\frac{\partial V}{\partial q}\right)$.

The speed of the wedge is $\dot{x}$ and the speed of the centre of mass of the cylinder is centre of mass of the cylinder is $\sqrt{\dot{s}^{2}+\dot{x}^{2}-2\dot{s}\dot{x}\cos\alpha}$ and the angular speed of the cylinder is $\frac{\dot{s}}{a}$.

The kinetic energy of the system is

$T\ =\ \frac{1}{2}m(\dot{s}^{2}+\dot{x}^{2}-2\dot{s}\dot{x}\cos\alpha)\ +\ \frac{1}{2}(mk^{2})\left(\frac{\dot{s}}{a}\right)\ +\ \frac{1}{2}M\dot{x}^{2}$,

or

$T\ =\ \frac{1}{2}m\left(1+\frac{k^{2}}{a^{2}}\right)\dot{s}^{2}\ -\ m\dot{s}\dot{x}\cos\alpha\ +\ \frac{1}{2}(m\ +\ M)\dot{x}^{2}$,

and the potential energy is

$V\ =\ \text{constant}\ -\ m\text{g}s\sin\alpha$

Application of Lagrange’s equation to the coordinate $x$ gives us

$\left(1+\frac{k^{2}}{a^{2}}\right)\ddot{s}=\ddot{x}\cos\alpha\ +\ \text{g}\sin\alpha$.

and application of Lagrange’s equation to the coordinate $s$ gives us

$m\ddot{s}\cos\alpha\ =\ (m+M)\ddot{x}$

Elimination of $\ddot{s}$ from these two equations gives us

$\ddot{x}=\frac{m\text{g}\sin\alpha\cos\alpha}{(m+M)\left(1+\frac{k^{2}}{a^{2}}\right)-m\cos^{2}\alpha}$

You can also easily find an expression for $\ddot{s}$ is you wish.

Exercise $\PageIndex{12}$

There is no acceleration normal to the plane, and therefore $N\ =\ m\text{g}\cos\alpha$. The frictional force $F$ acts along the tangent to the path and is equal to $\mu N$, or $\mu m\text{g}\cos\alpha$, where $\mu$ is the coefficient of moving friction. We are told to ignore the difference between the coefficients of moving and limiting static friction. Since the particle was originally at rest in limiting static friction, we must have $\mu\ =\ \tan\alpha$. Therefore $F\ =\ m\text{g}\sin\alpha$. The tangential equation of motion is

$m\ddot{s}\ =\ -F\ +$ whatever the component of $m\textbf{g}$ is in the tangential direction in the sloping plane.

The component of $m\textbf{g}$ down the plane would be (look at the left hand drawing) $m\text{g}\sin\alpha$, and so its tangential component (look at the right hand drawing) is $m\text{g}\sin\alpha\sin\psi$. So we have, for the tangential equation of motion,

$m\ddot{s}=-m\text{g}\sin\alpha\ +\ m\text{g}\sin\alpha\sin\psi$,

or

$\ddot{s}=-\text{g}\sin\alpha(1-\sin\psi)$.

We are seeking a relation between $V$ and $\psi$, so, in the now familiar fashion, we write $V\frac{dV}{ds}$ for $\ddot{s}$, so the tangential equation of motion is

$$V\frac{dV}{ds}=-\text{g}\sin\alpha(1-\sin\psi). \tag{1}\label{12.1}$$

We also need the equation of motion normal to the trajectory. The component of $m\textbf{g}$ in that direction is $m\text{g}\sin\alpha\cos\psi$, and so the normal equation of motion is

$\frac{mV^{2}}{\rho}\ =\ m\text{g}\sin\alpha\cos\psi$.

Here $\rho$ is the radius of curvature of the path, which is the reciprocal of the curvature $\frac{ds}{d\psi}$. The normal equation of motion is therefore

$$V^{2}\frac{d\psi}{ds}\ =\ \text{g}\sin\alpha\cos\psi. \tag{2}\label{12.2}$$

Divide Equation ($\ref{1}$) by Equation ($\ref{2}$) to eliminate $s$ and thus get a desired differential equation between $V$ and $\psi$:

$$\frac{1}{V}\frac{dV}{d\psi}\ =\ -\frac{(1-\sin\psi)}{\cos\psi}. \tag{3}\label{12.3}$$

This is easily integrated; a convenient (not the only) way is to multiply top and bottom by $1\ +\ \sin\psi$. In any case we soon arrive at

$$\ln V\ =\ -\ln(1+\sin\psi)\ +\ \text{constant}, \tag{4}\label{12.4}$$

and with the initial condition $V\ =\ V_{0}$ when $\psi\ =\ 0$, this becomes

$$\underline{\underline{V=\frac{V_{0}}{1+\sin\psi}}}. \tag{5}\label{12.5}$$

In the limit, as $\psi\rightarrow90^{\circ},\ V\rightarrow\frac{1}{2}V_{0}$. The particle is then moving at constant velocity and is in equilibrium under the forces acting upon it just when it was initially at rest.

Exercise $\PageIndex{13}$

13.

$M_{1}$ = mass of complete sphere of radius $a$.

$M_{1}$ = mass of missing inner sphere of radius $xa$.

$M$ = mass of given hollow sphere.

We have $M\ =\ M_{2}-M_{1}$ and $\frac{M_{2}}{M_{1}}=x^{3}$ and therefore

$M_{1}\ =\ \frac{M}{1-x^{3}}$ and $M_{2}\ =\ \frac{Mx^{3}}{1-x^{3}}$.

Also $I=\frac{2}{5}M_{1}a^{2}\ -\ \frac{2}{5}M_{2}x^{2}a^{2}\ =\ \frac{2}{5}a^{2}(M_{1}-M_{2}x^{2})$.

Hence $I=\frac{2}{5}Ma^{2}\times\frac{1-x^{5}}{1-x^{3}}$.

If $x=0,\ I\ =\ \frac{2}{5}Ma^{2}$, as expected. If $x\rightarrow1$, you may have to use de l’Hôpital’s rule to show that $I\rightarrow\frac{2}{5}Ma^ {2}$ as expected.

Exercise $\PageIndex{14}$

$M_{1}$ = mass of mantle.

$M_{2}$ = mass of core.

$M$ = mass of entire planet.

We have $M=M_{1}+M_{2}$ and $\frac{M_{1}}{M_{2}}=\frac{s(1-x^{3})}{x^{3}}$ and therefore

$M_{2}\ =\ M\times\frac{x^{3}}{x^{3}\ +\ s(1-x^{3})}$ and $M_{1}\ =\ M\times\frac{s(1-x^{3})}{x^{3}\ +\ s(1-x^{3})}$

Also

$I\ =\ I_{\text{core}}\ +\ I_{\text{mantle}}\ =\ \frac{2}{5}M_{2}x^{2}a^{2}\ +\ \frac{2}{5}M_{1}a^{2}\times\frac{1-x^{5}}{1-x^{3}}$,

where I have made use of the result from the previous problem. On substitution of the expressions for $M_{1}$ and $M_{2}$, we quickly obtain

$$I\ =\ \frac{2}{5}Ma^{2}\times\frac{s\ +\ (1-s)x^{5}}{s\ +\ (1-s)x^{3}} \tag{1}\label{14.1}$$

A hollow planet would correspond to $\frac{1}{s}=0$. Divide top and bottom by $s$ and it is immediately seen that the expression for a hollow planet would be identical to the expression obtained for the previous problem.

Note that both $x\ =\ 0$ and $x\ =\ 1$ correspond to a uniform sphere, so that in either case, $I\ =\ \frac{2}{5}Ma^{2}$ for all other cases, the moment of inertia is less than $\frac{2}{5}Ma^{2}$.

The core size for minimum moment of inertia is easily found by differentiation of the above expression for $I$, and the required expression follows after some algebra. For $s\ =\ 0.6$, the equation becomes $9-15x^{2}-4x^{5}\ =\ 0$, of which the only positive real root is $x\ =\ 0.73682$, which corresponds to a moment of inertia of 0.90376 % $\frac{2}{5}Ma^{2}$. Note that. for $s\ =\ 0.6$, the moment of inertia, expressed in units of $\frac{2}{5}Ma^{2}$ varies very little as the core size goes from 0 to 1, so that measurement of the moment of inertia places very little restriction on the possible core size.

The inverse of Equation ($\ref{1}$) is

$$(1-s)x^{5}\ -\ I(1-s)x^{3}\ +\ (1-I)s\ =\ 0, \tag{2}\label{14.2}$$

where $I$ is expressed in units of $\frac{2}{5}Ma^{2}$. For $I\ =\ 0.911$, there are two positive real roots (look at the graph); they are $x\ =\ 0.64753$ and $0.81523$. For $I\ =\ 0.929$, the roots are 0.55589 and 0.87863. Thus the core size could be anything between 0.55589 and 0.64753 or between 0.81523 and 0.87863 a rather large range of uncertainty. Even if $I$ were known exactly (which does not happen in science), there would be two solutions for $x$.

Exercise $\PageIndex{15}$

This is just a matter of geometry. If, when you make a small angular displacement, you raise the centre of mass of the brick the equilibrium is stable. For, while the brick is in its vertical position, it is evidently at a potential minimum, and you have to do work to raise the centre of mass. If, on the other hand, your action in making a small angular displacement results in a lowering of the centre of mass, the equilibrium is unstable.centre of mass of the brick the equilibrium is stable. For, while the brick is in its vertical position, it is evidently at a potential minimum, and you have to do work to raise the centre of mass. If, on the other hand, your action in making a small angular displacement results in a lowering of the centre of mass, the equilibrium is unstable.

When the brick is in its vertical position, the height $h_{0}$ of its centre of mass above the base of the semicylinder is justcentre of mass above the base of the semicylinder is just

$h_{0}\ =\ R\ +\ l$.

When it is displaced from the vertical by an angle $\theta$, the point of contact between brick and semicylinder is displaced by a distance $R\theta$, and, by inspection of the drawing, the new height $h$ is

$h\ =\ R\cos\theta\ +\ R\theta\sin\theta\ +l\cos\theta$.

$h-h_{0}\ =\ R\theta\sin\theta\ -\ (R+l)(1-\cos\theta)$.

If you Maclaurin expand this as far as $\theta^{2}$, you arrive at

$h-h_{0}\approx\frac{1}{2}(R-l)\theta^{2}$.

This is positive, and therefore the equilibrium is stable, if $l\ <\ R$, or $2l\ <\ 2R$, i.e. if the length of the brick is less than the diameter of the semicylinder.

Exercise $\PageIndex{16}$

As in the previous question, it is just a matter of geometry. If rolling the Thing results in raising its centre of mass, the equilibrium is stable. Initially, the height of the centre of mass is $H_{0}\ =\ b\ + l$.centre of mass, the equilibrium is stable. Initially, the height of the centre of mass is $H_{0}\ =\ b\ + l$.

After rolling, the dashed line, which joins the centres and is of length $a+b$, makes an angle $\theta$ with the vertical. The short line joining the centre of mass of the Thing to the centre of curvature of its bottom is of length $l-a$ and it makes an angle $\theta+\\phi$ with the vertical. The height of the centre of mass is therefore nowcentre of mass of the Thing to the centre of curvature of its bottom is of length $l-a$ and it makes an angle $\theta+\\phi$ with the vertical. The height of the centre of mass is therefore now

$h\ =\ (a+b)\cos\theta+(l-a)\cos(\theta+\phi)$

The centre of mass has therefore rise through a heightcentre of mass has therefore rise through a height

$h\ -\ h_{0}\ = (a+b)\cos\theta\ +\ (l-a)\cos(\theta+\phi)\ -b-l$.

Also, the two angles are related by $a\phi\ =\ b\theta$, so that

$h\ -\ h_{0}\ = (a+b)\cos\theta\ +\ (l-a)\cos\left[\left\{1+\left(\frac{b}{a}\right)\right\}\theta\right]\ -b-l$

$h\ -\ h_{0}\ = -\frac{1}{2}\theta^{2}[a+b\ +\ (l-a)(1+\frac{b}{a})^{2}]$.

For stability this must be positive, and hence $\frac{1}{l}\ >\ \frac{1}{a}\ +\ \frac{1}{b}$.

If $a\ =\ b$, this becomes $l\ <\ \frac{1}{2}a$.

For a hollow semicylinder,	$l\ =\ (1-\frac{2}{\pi})a=0.363a$	$\Box$ Stable
For a hollow hemisphere,	$l=0.5a$	$\Box$ Borderline stable
For a solid semicylinder,	$l\ =\ [1-\frac{4}{(3\pi)}]a=0.576a$	$\Box$ Unstable
For a solid hemisphere,	$l=\frac{5}{8}a=0.625a$	$\Box$ Unstable

Exercise $\PageIndex{17}$

We need to find the height $h$ of the centre of mass above the level of the pegs as a function of $\theta$. See drawing on next page.centre of mass above the level of the pegs as a function of $\theta$. See drawing on next page.

Angels:

$\text{BAC}\ =\ 45^{\circ}-\theta$

$\text{ABX}\ =\ 45^{\circ}+\theta$

Distances:

$\text{AB}\ =\ 2ka$

$\text{AC}\ =\ 2ka\ \cos(45^{\circ}-\theta)$

$\text{EF}\ =\ 2ka\ \cos(45^{\circ} -\theta)\cos(45^{\circ}+\theta)=ak\cos2\theta$

$\text{DC}\ =\ a\sqrt{2}$

$\text{DF}\ =\ a\sqrt{2}\cos\theta$

$h\ =\ \text{DF}\ -\ \text{EF}\ =\ a(\sqrt{2}\cos\theta-k\cos2\theta)$

$h_{0}=$ height of centre of mass above pegs when $\theta = 0$ centre of mass above pegs when $\theta\ =\ 0^{\circ}\ =\ a(\sqrt{2}-k)$

$y\ =\ \frac{h}{h_{0}}\ =\frac{\sqrt{2}\cos\theta-k\cos2\theta}{\sqrt{2}-k}$

Exercise $\PageIndex{18}$

There are three forces acting on the hemisphere: Its weight $m\text{g}$. The reaction $N$ of the wall, which is perpendicular to the wall since the wall is smooth. The reaction $R$ of the floor, which acts at an angle $\lambda$ to the floor, where $\mu\ =\ \tan\lambda$. Three forces in equilibrium must act through a point; therefore all three forces act through the point $P$. It is thus clear that

$\sin\ \theta\ =\ \frac{\text{OP}}{\text{OC}}\ =\ \frac{a\mu}{\frac{3}{8}a}\ =\ \frac{8\mu}{3}$.

If $\mu\ =\ \frac{1}{4},\ \theta\ =\ 41^{\circ}48'$. If $\mu\ =\ \frac{3}{8},\ \theta\ =\ 90^{\circ}$. If $\mu\ >\ \frac{3}{8}$ the hemisphere can rest in any position, the equilibrium not being limiting static equilibrium.

Exercise $\PageIndex{19}$

This solution uses the same method that Professor Marsh (Warwick University) showed me for Problem 20. I believe it to be clearer than an earlier solution that I had posted.

At an instant when the rod is tilted at angle $\theta$, the coordinates of C with respect to the fixed point O are:

$$\overline{x}\ =\ a(\sin\theta\ -\ \theta\cos\theta), \tag{1}\label{19.1}$$

$$\overline{y}\ =\ a(\cos\theta\ +\ \theta\sin\theta) \tag{2}\label{19.2}$$

and so its velocity components are

$$\dot{\overline{x}}\ =\ a\theta\sin\theta\dot{\theta} \tag{3}\label{19.3}$$

and

$$\dot{\overline{y}}\ =\ a\theta\cos\theta\dot{\theta}. \tag{4}\label{19.4}$$

The moment of inertia of the rod about the centre of mass is $\frac{1}{3}ml^{2}$.

The kinetic energy $T$ is the sum of the translational kinetic energy and the rotational kinetic energy about the centre of mass:centre of mass:

$$T\ =\ \left(\frac{1}{2}a^{2}\theta^{2}\ +\ \frac{1}{6}l^{2}\right)m\dot{\theta}^{2}, \tag{5}\label{19.5}$$

and the potential energy $V$ is

$$V\ =\ m\text{g}a(\cos\ \theta\ +\ \theta\sin\ \theta). \tag{6}\label{19.6}$$

One can now get the equation of motion either by Lagrangian means or by equating the derivative with respect to $\theta$ of the total energy to zero, since there are no nonconservative forces and hence the total energy is independent of $\theta$. In carrying out the differentiation, note that $\frac{d}{d\theta}\dot{\theta}^{2}\ =\ 2\dot{\theta}\frac{d\dot{\theta}}{d\theta}\ =\ 2\ddot{\theta}$. We obtain, for the equation of motion:

$$a^{2}\theta\dot{\theta}^{2}\ +\ (a^{2}\theta^{2}+\frac{2}{3}l^{2})\ddot{\theta}\ +\ \text{g}a\theta\cos\theta\ =\ 0 \tag{7}\label{19.7}$$

For small $\theta$ (neglecting second and higher powers of $\theta$), $\cos\theta\rightarrow 1$ and $a^{2}\theta^{2}$ is negligible compared with $l^{2}$, so the equation of motion becomes, approximately, $\ddot{\theta}=-\frac{3\text{g}a}{l^{2}}$, and so the period is $\underline{\underline{P\ =\ \frac{2\pi l}{\sqrt{3\text{g}a}}}}$.

Exercise $\PageIndex{20}$

I am much indebted to Professor T. R. Marsh of Warwick University not only for finding a mistake in an earlier posted solution to this problem, but for providing the following solution.

$$I\ =\ ma^{2}\left(\frac{7}{5}\ -\ \frac{3}{4}\cos\theta\right). \tag{2}\label{20.2b}$$

$x\ =\ \frac{3a\theta}{8}$

We are going to refer the motion to a fixed point Q, which is the point of contact between hemisphere and table when the hemisphere is in its equilibrium position.

At an instant when the hemisphere is tilted at an angle $\theta$, the distance between A and Q is $a\theta$, and the coordinates of C relative to Q are

$$\overline{x}\ =\ a\theta\ -\ \frac{3}{8}a\sin\theta, \tag{1}\label{20.1}$$

$$\overline{y}\ =\ a -\ \frac{3}{8}a\cos\theta. \tag{2}\label{20.2}$$

Therefore the velocity components of C are

$$\dot{\overline{x}}\ =\ a\left(1-\frac{3}{8}\cos\theta\right)\dot{\theta}, \tag{3}\label{20.3}$$

$$\dot{\overline{y}}\ =\ \frac{3}{8}a\sin\theta\dot{\theta}. \tag{4}\label{20.4}$$

By the parallel axes theorem, the moment of inertia around the centre of mass iscentre of mass is

$$I\ =\ \frac{2}{5}ma^{2}\ -\ m\left(\frac{3}{8}a\right)^{2}\ =\ \frac{83}{320}ma^{2} \tag{5}\label{20.5}$$

The kinetic energy $T$ is the sum of the translational kinetic energy and the rotational kinetic energy about the centre of mass:centre of mass:

$$T\ =\ \frac{1}{2}ma^{2}\left[\left(1-\frac{3}{8}\cos\theta\right)^{2}\ +\ \left(\frac{3}{8}\sin\theta\right)^{2}\ +\ \frac{83}{230}\right]\dot{\theta}^{2}\ =\ ma^{2}\left(\frac{7}{10}-\frac{3}{8}\cos\theta\right)\dot{\theta}^{2} \tag{6}\label{20.6}$$

The potential energy $V$ is

$$V\ =\ m\text{g}a(1-\frac{3}{8}\cos\theta). \tag{7}\label{20.7}$$

We can the get the equation of motion either by using the Lagrangian equations, or by calculating the derivative with respect to $\theta$ of the total energy $T\ +\ V$. The derivative is zero, because there are no nonconservative forces and total energy is constant. Note that (as in Problem 19) the derivative of $\dot{\theta}^{2}$ with respect to $\theta$ is $2\dot{\theta}\frac{d\dot{\theta}}{d\theta}$, which is $2\ddot{\theta}$. Either method results in the equation of motion:

$$\left(\frac{7}{5}\ -\ \frac{3}{4}\cos\theta\right)\ddot{\theta}\ + \frac{3}{8}\sin\theta\dot{\theta}^{2}\ + \frac{3}{8}\text{g}\sin\theta\ = 0. \tag{8}\label{20.8}$$

In the small angle limit, $\cos\theta\rightarrow 1$, and $\sin\theta\rightarrow \theta$ is negligible compared with $\text{g}$, so the equation of motion becomes

$$\ddot{\theta}\ =\ -\frac{15\text{g}}{26a}\theta \tag{9}\label{20.9}$$

$$\underline{\underline{P\ =\ 2\pi\sqrt{\frac{26a}{15\text{g}}}}}. \tag{10}\label{20.10}$$

Exercise $\PageIndex{21}$

The (second) moment of inertia with respect to the centre (see centre (see Section 2.19 of Chapter 2) is

$I_{\text{centre}} = 4 \pi \rho_0 \int^a_0 (r^4-r^5/a)dr = \frac{2}{15}\pi\rho_0a^5.$.

The moment of inertia with respect to an axis through the centre is 2/3 of this:centre is 2/3 of this:

$I_{\text{axis}}\ =\ \frac{4}{45}\pi\rho_{0}a^{5}$.

$\therefore \qquad \qquad \qquad \underline{\underline{I_{\text{axis}}\ =\ \frac{4}{15}Ma^{2}}}$.

Exercise $\PageIndex{22}$

Left-hand particle:$T\ =\ m\text{g}[\mu\cos(\alpha-\theta)\ +\ \sin(\alpha-\theta)]$.

Right-hand particle:$T\ =\ m\text{g}[\sin(\alpha+\theta)\ -\ \mu\cos(\alpha+\theta)]$.

$\therefore \qquad \mu[\cos(\alpha-\theta)\ +\ \cos(\alpha+\theta)]\ =\ \sin(\alpha+\theta)\ -\ \sin(\alpha-\theta)$,

and, by the “sum and difference” trigonometrical formulae, we obtain

$2\mu\cos\alpha\cos\theta\ =\ 2\cos\alpha\sin\theta,$

from which

$\underline{\underline{\tan\ \theta\ =\ \mu.}}$

Exercise $\PageIndex{23}$

Consider a portion of the rope between $\theta$ and $\delta\theta$. There are four forces on this portion. The tension $T$ at $\theta$. The tension $T\ +\ \delta T$ at $\theta\ +\ \delta\theta$ ($\delta T$ is negative). The normal reaction $\delta N$ of the cylinder on the rope. The frictional force $\mu\delta N$ of the cylinder on the rope. Note that the rope is about to slip downwards, so the friction force is upwards as shown.

We have

$\delta N\ =\ (2T\ +\ \delta T)\sin\left(\frac{1}{2}\theta\right)$

and

$(T\ +\ \delta T)\cos\left(\frac{1}{2}\delta\theta\right)\ +\ \mu\delta N\ =\ T\cos\left(\frac{1}{2}\delta\theta\right)$.

To first order, these become

$\delta N\ =\ T\delta\theta$

$\delta T\ =\ -\mu\delta N$

and

$\delta T\ =\ -\mu T\delta\theta$

and hence by integration

$\underline{\underline{F\ =\ M\text{g}e^{-\mu\alpha}}}$.

Exercise $\PageIndex{24}$

Area of square = $4a^{2}$

Area of rectangle = $4a^{2}(1-x)$

Area of triangle = $2a^{2}(x+y-1)$

Area of trapezoid = $2a^{2}(1-x+y)$

The weight of the cube is $8a^{3}\rho s\text{g}$, and it acts downward through C, the centre of mass. The hydrostatic upthrust is $4a^{3}(1-x+y)\rho\text{g}$ and it acts upward through the centre of buoyancy H. Here $\rho$ is the density of the fluid, and $\rho s$ is the density of the wood. We evidently must find the centre of mass. The hydrostatic upthrust is $4a^{3}(1-x+y)\rho\text{g}$ and it acts upward through the centre of buoyancy H. Here $\rho$ is the density of the fluid, and $\rho s$ is the density of the wood. We evidently must find the $X'-$ coordinate of C and of H. Let’s first of all find the $X-$ and $Y-$ coordinates (see the next figure).

The $X-$ and $Y-$coordinates of C are trivial and quite easy respectively:

$X_{C}\ =\ a \qquad \qquad Y_{C}\ =\ a(1-2x)$

You are going to have to work quite hard at it to find the $X-$ and $Y-$ coordinates of H, the centre of buoyancy, which is the centroid of the trapezoid. “After some algebra” you should findcentre of buoyancy, which is the centroid of the trapezoid. “After some algebra” you should find

$X_{H}\ =\ \frac{2(1-x+2y)a}{3(1-x+y)} \qquad \qquad Y_{H}\ =\ \frac{2(2-4x+2y+2x^{2}-2xy-y^{2})a}{3(1-x+y)}$

To find the $X'-$ coordinates of C and of H, we use the usual formulas for rotation of axes, being sure to get it the right way round:

$\begin{pmatrix}X'\\Y'\end{pmatrix}\ =\ \begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix}$,

together with

$\tan\ \theta\ =\ x\ +\ y-1$.

Take moments about the axle (origin):

$8a^{3}\rho s\text{g}X'_{C}\ =\ 4a^{3}\rho\text{g}(1-x+y)$.

After a little more algebra, you should eventually arrive at

$\underline{\underline{s=\frac{3-7x+2y+6x^{2}-3y^{2}-2x^{3}+y^{3}+3xy^{2}}{3(2-3x-y+2x^{2}+2xy)}}}$

Exercise $\PageIndex{25}$

Let the radii of the cylinder and sphere be $a$ and $b$ respectively, and the mass of the sphere be $M$. The angles $\theta$ and $\phi$ are related by $a\theta\ =\ b\phi$. I have drawn the three forces on the sphere, namely its weight, the normal reaction of the cylinder on the sphere, and the frictional force on the sphere. The transverse acceleration of the centre of the sphere is $(a+b)\ddot{\theta}$ and the centripetal acceleration is $(a+b)\dot{\theta}^{2}$. The equations of motion are:centre of the sphere is $(a+b)\ddot{\theta}$ and the centripetal acceleration is $(a+b)\dot{\theta}^{2}$. The equations of motion are:

$$M\text{g}\sin\theta\ -\ F\ =\ M(a+b)\ddot{\theta} \tag{1}\label{25.1}$$

and

$$M\text{g}\cos\theta\ -\ N\ =\ M(a+b)\dot{\theta}^{2} \tag{2}\label{25.2}$$

The angular acceleration of the sphere about its centre is $\ddot{\theta}\ +\ \ddot{\phi}\ =\ \left(1+\frac{a}{b}\right)\ddot{\theta}$, and its rotational inertia is $\frac{2Mb^{2}}{5}$. The torque that is causing this angular acceleration is $Fb$, and therefore the rotational equation of motion is

$$Fb =\ \frac{2}{5}Mb^{2}\left(1+\frac{a}{b}\right)\ddot{\theta} \tag{3}\label{25.3}$$

Elimination of $F$ between Equations ($\ref{20.1}$) and ($\ref{20.3}$) yields

$$\ddot{\theta} = \frac{5\text{g}}{7(a+b)}\sin\theta. \tag{4}\label{20.4}$$

Write $\ddot{\theta}$ as $\dot{\theta}\frac{d\dot{\theta}}{d\theta}$ in the usual way and integrate with initial conditions $\theta=\dot{\theta}=0$ or from energy considerations:

$$\dot{\theta}^{2} =\frac{10\text{g}}{7(a+b)}(1-\cos\theta) \tag{5}\label{20.5}$$

Substitute for $\ddot{\theta}$ and $\dot{\theta}^{2}$ into Equation ($\ref{20.2}$) to obtain

$$N =\ M\text{g}(17\cos\theta-10). \tag{6}\label{20.6}$$

This is zero, and the sphere leaves the cylinder, when $\cos\theta\ =\ \frac{10}{17}$, $\theta\ =\ 53^{\circ}58'$.

Exercise $\PageIndex{26}$

Surface density = $\sigma$ g cm^-2

Original sandwich:

Mass = 54$\sigma$ g

$x$-coordinate of centre of mass = 3 cm centre of mass = 3 cm

$y$-coordinate of centre of mass = 4 cm centre of mass = 4 cm

Bite:

Mass = $\frac{1}{2}\pi3^{2}\sigma$ =14.137 166 94$\sigma$ g

Distance of centre of mass from hypotenuse = centre of mass from hypotenuse= $\frac{4}{3\pi}\times 3\ =\ \frac{4}{\pi}$ = 1.273 239 545 cm

x-coordinate of centre of mass = 4.5 -centre of mass = $4.5\ -\ \frac{4}{\pi}\sin\theta=4.5-\frac{16}{5\pi}$ = 3.481 408 364 cm

y-coordinate of centre of mass = 6- centre of mass = $6\ -\ \frac{4}{\pi}\cos\theta\ =\ 6-\frac{12}{5\pi}$ = 5.236 056 273 cm

Remainder:

Mass = (54 - 14.137 166 94)$\sigma$ = 39.862 833 06$\sigma$ g

$x$-coordinate of centre of mass = $\overline{x}$centre of mass = $\overline{x}$

$y$-coordinate of centre of mass = $\overline{y}$centre of mass = $\overline{y}$

Moments:

39.862 833 06$\overline{x}$ + 14.137 166 94 × 3.481 408 364 = 54 × 3. $\underline{\underline{\overline{x} = 2.829\ 270\ 780\ \text{cm}}}$

39.862 833 06$\overline{y}$ + 14.137 166 94 × 5.236 056 273 = 53 × 4. $\underline{\underline{\overline{y}\ =\ 3.561\ 638\ 436\ \text{cm}}}$

This point is very close to the edge of the bite. The centre of the bite is at (4.5, 6), and its radius is 3. Its equation is thereforecentre of the bite is at (4.5, 6), and its radius is 3. Its equation is therefore

$(x-4.5)^{2}\ +\ (y-6)^{2}\ =9,$ or $x^{2}\ +\ y^{2}\ -9x\ -12y\ +\ 47.25=0$.

The line $x$ = 2.829 270 780 cuts the circle where $y^{2}-12y\ +\ 29.791\ 336\ 13\ =\ 0$. The lower of the two points of intersection is at $y$ = 3.508 280 941 cm. The centre of mass is slightly higher than this and is therefore just inside the bite.centre of mass is slightly higher than this and is therefore just inside the bite.

Exercise $\PageIndex{27}$

Consider a portion of the band within the angle $\delta\theta$. Its mass is $\frac{m\delta\theta}{2\pi}$ When the band is spinning at angular speed $\omega$ and its radius is $r$, the centrifugal force on that portion is $\delta F\ =\ \frac{mr\omega^{2}\delta\theta}{2\pi}$. (I leave it to the philosophers and the schoolteachers to debate as to whether there “really” is “such thing” as centrifugal force – I want to get this problem done, and I’m referring to a co-rotating frame.) The $y$-component of this force is $\frac{mr\omega^{2}\delta\theta}{2\pi}$. Also, the tension in the band when its radius is $r$ is $T=2\pi k(r-a)$.

Consider the equilibrium of half of the band. The $y$-component of the centrifugal force on it is $\frac{mr\omega^{2}}{2\pi}\int_{-\frac{\pi}{2}}^{+\frac{\pi}{2}}\cos\theta d\theta=\frac{mr\omega^{2}}{\pi}$. The opposing force is $2T\ =\ 4\pi k(r-a)$. Equating these gives $\underline{\underline{\omega^{2}\ =\ \frac{4\pi^{2}k(r-a)}{mr}}}$.

Exercise $\PageIndex{28}$

Let the distance AB be $l$ and the distance AC be $c$. Let the mass of the rod be $m$.

Consider an elemental portion $\delta x$ of the rod at P at a distance $x$ from A. Its weight is $\frac{m\delta x}{l}$. When the rod is about to move, it will experience a frictional force $\delta f\ =\ \frac{\mu m\text{g}\delta x}{l}$, which will be in the direction shown if P is to the left of C, and in the opposite direction if P is to the right of C. When the rod is just about to move (but has not yet done so) it is still in equilibrium. Consider the moment about A of the frictional forces on the rod. The clockwise moment of the frictional forces on AC must equal the counterclockwise moment of the frictional forces on CB. Thus

$\frac{\mu m\text{g}}{l}\int_{0}^{c}x\ dx=\frac{\mu m\text{g}}{l}\int_{c}^{l}x\ dx$.

$\therefore \qquad\qquad \underline{\underline{c=\frac{l}{\sqrt{2}}}}$.

The net force on the rod is

$F\ -\ \frac{\mu m\text{g}}{l}\int_{0}^{c}dx\ +\ \frac{\mu m\text{g}}{l}\int_{c}^{l} dx$,

and this is zero, and therefore

$\underline{\underline{F\ =\ \frac{\mu m\text{g}(2c-l)}{l}=(\sqrt{2}-1)\mu m\text{g}.}}$

Exercise $\PageIndex{29}$

The cone slips when $\tan\theta\ >\ \mu$.

It tips when C (the centre of mass) is to the left of M. centre of mass) is to the left of M.

The distance OC is $\frac{h}{4}$. (See Chapter 1, Section 1.7). Therefore it tips when $\tan\theta>4\frac{a}{h}$.

Thus it slips if $\mu<4\frac{a}{h}$ and it tips if $\mu<4\frac{a}{h}$.

Exercise $\PageIndex{30}$

When the block is just about to tip, the reaction of the table on the block acts at A and it is directed towards the point K, because, when three coplanar forces are in equilibrium they must act through a single point. The angle $\lambda$ is given by $\tan\lambda\ =\ \frac{a}{x}$. However, by the usual laws of friction, the block will slip as soon as $\tan\lambda\ =\ \mu$. Thus the block will slip if $\mu<\frac{a}{x}$, and it will tip if $\mu>\frac{a}{x}$. Expressed otherwise, it will slip if $x<\frac{a}{\mu}$ and it will tip if $x>\frac{a}{\mu}$. The greatest possible value of $x$ is $2a$; therefore the block will inevitably slip if $\mu < \frac{1}{2}$

Exercise $\PageIndex{31}$

+

When or if the cylinder is just about to tip, it is about to lose contact with the left hand peg. The only forces on the cylinder are the torque, the weight, and the reaction $R$ of the right hand peg on the cylinder, which must be vertical and equal to $m\text{g}$. But the greatest possible angle that the reaction $R$ can make with the surface of the cylinder is the angle of friction $\lambda$ given by $\tan\ \lambda\ =\ \mu$. From geometry, we see that $\sin\ \theta\ =\ k$, or $\tan\ \theta\ =\ \frac{k}{\sqrt{1-k^{2}}}$. Thus the cylinder will slip before it tips if $\mu\ <\ \frac{k}{\sqrt{1-k^{2}}}$ and it will tip before it slips if $\mu\ >\ \frac{k}{\sqrt{1-k^{2}}}$.

If the cylinder tips (which it will do if $\mu\ >\ \frac{k}{\sqrt{1-k^{2}}}$), the clockwise torque t at that moment will equal the counterclockwise torque of the couple ($R$ and $m\text{g}$), which is $m\text{g}ka$. Thus the torque when the cylinder tips is

TIP:

$$\tau\ =\ m\text{g}ak. \tag{1}\label{31.1}$$

When or if the cylinder is just about to slip, the forces are as shown above, in which I have resolved the reactions of the pegs on the cylinder into a normal reaction (towards the axis of the cylinder) and a frictional force, which, when slipping is about to occur, is equal to m times the normal reaction. The equilibrium conditions are

$\mu(N_{1}\ +\ N_{2})\cos\theta\ +\ (N_{1}-N_{2})\sin\theta\ =\ 0$,

$\mu(N_{1}\ -\ N_{2})\sin\theta\ -\ (N_{1}+N_{2})\cos\theta\ +\ m\text{g}=\ 0$

and

$\mu(N_{1}\ +\ N_{2})a\ =\ \tau$.

We can find $N_{1}\ +\ N_{2}$ by eliminating $N_{1}\ -\ N_{2}$ from the first two equations, and then, writing $\sqrt{1-k^{2}}$ for $\cos\theta$, we find that, when slipping is about to occur,

SLIP:

$$\tau\ =\ m\text{g}a\ \times\ \frac{\mu}{1+\mu^{2}}\ \times\ \frac{1}{\sqrt{1-k^{2}}}. \tag{2}\label{31.2}$$

I have drawn below the functions

$\frac{\tau}{m\text{g}a}\ =\ k\ \text{(tip) and}\ \frac{\tau}{m\text{g}a}\ =\ \frac{\mu}{1\ +\ \mu^{2}}\times\frac{1}{\sqrt{1-k^{2}}}\ \text{(slip)}$

for $k\ =\ 0.1,\ 0.3,\ 0.5,\ \frac{1}{\sqrt{2}}$ and $0.9$. The horizontal lines are the tip functions, and the curves are the slip functions. As long as $\mu\ <\ \frac{k}{\sqrt{1-k^{2}}}$ the cylinder will slip. As soon as $\mu\ <\ \frac{k}{\sqrt{1-k^{2}}}$ the cylinder will tip.

Exercise $\PageIndex{32}$

We’ll leave to the philosophers the question as to whether centrifugal force “really exists”, and we’ll work in a co-rotating reference frame, so that the car, when referred to that frame, is in static equilibrium under the six forces shown. Clearly, $N_{1}$ and $N_{2}\ =\ m\text{g}$ and $F_{1}\ +\ F_{2}\ =\ \frac{mv^{2}}{R}$.

The car slips when $F_{1}\ +\ F_{2}\ =\ \mu(N_{1}+N_{2})$; that is, when $v\ =\ \sqrt{\mu\text{g}R}$.

The car tips when $\frac{mv^{2}h}{R}\ =\ m\text{g}d;$ that is, when $v\ =\ \sqrt{\frac{d\text{g}R}{h}}$.

That is, it will slip or tip according as to whether $\mu\ < \frac{d}{h}$ or $> \frac{d}{h}$.

For example suppose $d\ =\ 60\ \text{cm},\ h\ =\ 60\ \text{cm},\ \text{g}\ =\ 9.8\ \text{m s}^{-2},\ R\ =\ 30\ \text{m},\ \mu\ =\ 0.8$.

In that case, $\frac{d}{h}\ =\ 0.75$, so it will tip at $v\ =\ 14.8\ \text{m s}^{-1}\ =\ 53.5\ \text{km hr}^{-1}$.

But if it rains, reducing $\mu$ to 0.7, it will slip at $v\ =\ 14.3\ \text{m s}^{-1}\ =\ 51.6\ \text{km hr}^{-1}$.

Exercise $\PageIndex{33}$

I have drawn in green the radial and transverse components of the acceleration of the centre of mass $a\dot{\theta}^{2}$ and $a\ddot{\theta}$ respectively. I have drawn in red the weight of the rod and the normal and frictional components of the force of the table on the rod at $A$, $N$ and $F$ respectively.centre of mass $a\dot{\theta}^{2}$ and $a\ddot{\theta}$ respectively. I have drawn in red the weight of the rod and the normal and frictional components of the force of the table on the rod at $A$, $N$ and $F$ respectively.

The following are the equations of motion:

Normal:

$$ma\ddot{\theta}\ =\ m\text{g}\cos\theta\ -\ N. \tag{1}\label{33.1}$$

Lengthwise:

$$ma\dot{\theta}^{2}\ =\ -m\text{g}\sin\theta\ +\ F. \tag{2}\label{33.2}$$

Rotation:

$$k^{2}\ddot{\theta}\ =\ \text{g}a\cos\theta \tag{3}\label{33.3}$$

Here $k$ is the radius of gyration about A, given by

$$k^{2}\ =\ \frac{1}{3}l^{2}\ +\ a^{2}. \tag{4}\label{33.4}$$

From Equations ($\ref{33.1}$), ($\ref{33.3}$) and ($\ref{33.4}$), we obtain

$$N\ =\ m\text{g}\cos\theta.\left(\frac{l^{2}}{l^{2}\ +\ 3a^{2}}\right). \tag{5}\label{33.5}$$

The space integral (see Chapter 6, Section 6.2) of Equation ($\ref{33.3}$), with initial condition $\dot{\theta}\ =\ 0$ when $\theta\ =\ 0$, results in

$$\dot{\theta}^{2}\ =\ \frac{2\text{g}a}{k^{2}}\sin\theta. \tag{6}\label{33.6}$$

This can also be obtained by equation the loss of potential energy, $m\text{g}a\sin\theta$ to the gain in kinetic energy, $\frac{1}{2}mk^{2}\dot{\theta}^{2}$.

Combining this with Equations ($\ref{33.2}$) and ($\ref{33.4}$) leads to

$$F\ =\ m\text{g}\sin\theta.\left(\frac{l^{2}\ +\ 9a^{2}}{l^{2}\ +\ 3a^{2}}\right). \tag{7}\label{33.7}$$

At the instant of slipping, $F\ =\ \mu N$, and hence, from Equations ($\ref{33.5}$) and ($\ref{33.7}$) we find

$\tan\theta\ =\ \frac{\mu}{1\ +\ 9(\frac{a}{l})^{2}}$.

Exercise $\PageIndex{34}$

I derive $v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}$ by two different methods – one from energy considerations, the other from angular momentum considerations. First, energy.

If the table top is taken to be the zero level for potential energy, the initial potential energy was $-\frac{1}{2}m.\text{g}.\frac{1}{4}l\ =\ -\frac{1}{8}m\text{g}l$.

When the length of the dangling portion is $\frac{1}{2}l\ +\ x$ the potential energy is

$-\left(\frac{\frac{1}{2}l\ +\ x}{l}\right)m.\text{g}.\frac{1}{2}\left(\frac{1}{2}l\ +\ x\right)\ =\ -\frac{m\text{g}}{2l}\left(\frac{1}{2}l\ +\ x\right)^{2}\ =\ -\frac{1}{8}m\text{g}l\ -\ \frac{1}{2}m\text{g}l\ -\ \frac{m\text{g}x^{2}}{2l}$.

The loss of potential energy is therefore $\frac{1}{2}m\text{g}x\ +\ \frac{m\text{g}x^{2}}{2l}$.

This is equal to the gain in kinetic energy $\frac{1}{2}mv^{2}$, and therefore

$v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}$.

Another method:

Considera un punto A. Cualquier lugar servirá, pero yo lo he elegido para que sea una distancia$l$ below the level of the table and $l$ to the left of the table edge. The moment of momentum (= angular momentum) of the chain about this point is $mlv\ =\ ml\dot{x}$ and its rate of change is therefore $mlv\ =\ ml\dot{x}$. The torque about A is $\left(\mlv\ =\ ml\dot{x}$ and its rate of change is therefore $mlv\ =ml\dot{x}$. The torque about A is $\left(\frac{\frac{1}{2}l\ +\ x}{l}\right)m\text{g}l\ =\ \left(\frac{1}{2}l\ +\ x\right)m\text{g}$. These are equal, and so $l\ddot{x}\ =\ \text{g}\left(\frac{1}{2}l\ +\ x\right)$. Write $\ddot{x}\ =\ v\frac{dv}{dx}$ in the usual way, and integrate (with $v=0$ when $x=0$) and the result $v^{2}\ =\ \text{g}x\ +\ \frac{g}{l}x^{2}$ follows.

To find the relation between $x$ and $t$ we can use the energy Equation 9.2.9 for conservative systems

$t\ =\ \sqrt{\frac{m}{2}}\int_{x_{0}}^{x}\frac{dx}{\sqrt{E-V(x)}}$.

Here $x_{0}\ =\ 0$ and we have already seen that $E\ -\ V(x)\ =\ \frac{m\text{g}}{2l}x^{2}\ +\ \frac{m\text{g}x}{2}$. Upon integrating this expression, we obtain, after a little algebra and calculus,

$$\tag{1}\label{34.1}$$

The converse of this is the required expression

$$\tag{2}\label{34.2}$$

Differentiation of this with respect to time produces the third required expression:

$$\tag{3}\label{34.3}$$

You may verify from these last two equations, if you wish, that $v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}$.

The chain falls completely off the table when $x\ =\ \frac{1}{2}l$. That is (by using Equation ($\ref{34.1}$)), at time $\sqrt{\frac{l}{g}}\ln(2\ +\ \sqrt{3})\ =\ 1.317\sqrt{\frac{l}{\text{g}}}$.

If we express distances in units of $l$, time in units of $\sqrt{\frac{l}{\text{g}}}$ and therefore necessarily speeds in units of $\sqrt{\text{g}l}$, Equations ($\ref{34.2}$) and ($\ref{34.3}$) become

$$x\ =\ \frac{(e^{t}-1)^{2}}{4e^{t}}\ =\ \frac{1}{4}(e^{t}\ +\ e^{-t}-2)\ =\ \frac{1}{2}(\cosh t-1) \tag{4}\label{34.4}$$

$$v\ =\ \frac{e^{2t}-1}{4e^{t}}\ =\ \frac{1}{2}\sinh\ t \tag{5}\label{34.5}$$

and we can get the acceleration by a further differentiation:

$$a\ =\ \frac{1}{4}(e^{t}\ +\ e^{-t})\ =\ \frac{1}{2}\cosh\ t. \tag{6}\label{34.6}$$

We are pleased to note that, by the time that $x\ =\ \frac{1}{2}l$ [i.e. when the chain completely leaves the table at time $t\ =\ \ln(2\ +\ \sqrt{3})\sqrt{\frac{l}{\text{g}}}$ ], the acceleration is $\text{g}$. The speed is then $\sqrt{\frac{3}{4}l\text{g}}\ =\ 0.866\sqrt{l\text{g}}$.

Exercise $\PageIndex{35a}$

The maximum overhang of book $\bf{1}$ is $d_{1}\ =\ w$.

The centre mass of $\bf{1\ +\ 2}$centre mass of $\bf{1\ +\ 2}$ is at $\frac{3w}{2}$ from the left hand side (LHS) of $\bf{2}$, so $d3\ =\ \frac{w}{3}$.

The distance of the centre of mass of $\bf{1+2+3}$centre of mass of $\bf{1+2+3}$ is at $\frac{5\text{w}}{2}$ from the LHS of $\bf{3}$, so $d3\ =\ \frac{w}{3}$.

Thus $D\ =\ d_{1}\ +\ d_{2}\ +\ d_{3}\ =\ \left(1\ +\ \frac{1}{2}\ +\ \frac{1}{3}\right)\text{w}\ =1.8\dot{3}\text{w}$.

Exercise $\PageIndex{35b}$

In a similar manner we find that, given $n\ +\ 1$ books, the maximum overhang is

$D\ =\ \left(1+\frac{1}{2}+\frac{1}{3}...\ ...+\frac{1}{n}\right)\text{w}$.

I do not know if there is a simple expression for the sum to $n$ terms of this harmonic series. Please let me know if you know of one or can find one. Therefore I used a computer to solve

$1+\frac{1}{2}+\frac{1}{3}...\ ...+\frac{1}{n}\ =\ 10$

by brute force. I got $n = 12367$, so you would need 12368 books.

Exercise $\PageIndex{35c}$

The harmonic series is divergent and has no finite limit, so there is no finite limit to the possible overhang.

You might wish to speculate on any practical limitations on constructing such a pile of books. For example, we have been assuming a uniform gravitational field – but this will no longer be valid once the overhang becomes comparable to the radius of Earth. This will, however, need quite a large number of books.

Exercise $\PageIndex{36}$

In the solution that follows, a prime will be used to denote differentiation with respect to $x$, and $p\ =\ y'\ =\ \frac{dy}{dx}$. I shall also make use of an auxiliary variable $\phi\ =\ \sinh^{-1}p$. The initial conditions are $y=0,\ x=a,\ p=0,\ \phi=0$. The final conditions are $x=0,\ p=-\infty,\phi=-\infty,y$ to be determined.

At time $t$, the $y-$coordinate of the Man is $v\ t$. If $(x,\ y)$ are the coordinates of the Dog at that time, the slope of the path taken by the Dog is

$$p\ =\ -\frac{vt-y}{x}, \tag{1}\label{36.1}$$

so that

$$v\ t\ =\ y-px. \tag{2}\label{36.2}$$

The speed of the Dog is

$$A v =\ -\frac{ds}{dt}\ =\ -\sqrt{1+p^{2}}\frac{dx}{dt}. \tag{3}\label{36.3}$$

[This comes from $ds\ =\ \sqrt{1+\left(\frac{dy}{dx}\right)^{2}}dx$. The minus sign is necessary because $\left(\frac{dx}{dt}\right)$ is negative, and $Av$, the speed (not velocity!) of the Dog is necessarily positive.]

Now $\left(\frac{dx}{dt}\right)\ =\ -\frac{1}{t'}$ so Equation ($\ref{eq:36.3}$) can be written

$$Avt'\ =\ -\sqrt{1+p^{2}} \tag{4}\label{36.4}$$

If we can eliminate $t$ between Equations ($\ref{36.2}$) and ($\ref{36.4}$), we will obtain a relation between the slope $p$ and $x$, and hence potentially a relation between $y$ and $x$.

Differentiate Equation ($\ref{eq:36.2)}$ with respect to $x$ (recalling that $y'=p$):

$$vt'\ =\ -p'x \tag{5}\label{36.5}$$

It is now simple to eliminate $t'$ from Equations ($\ref{36.4}$) and ($\ref{36.5}$):

$$Ap'x\ =\ \sqrt{1+p^{2}} \tag{6}\label{36.6}$$

On separating the variables and integrating, we obtain

$$A\int\frac{dp}{\sqrt{1+p^{2}}}\ =\ \int\frac{dx}{x}. \tag{7}\label{36.7}$$

With initial conditions $p=0$ when $x=a$, this gives us

$$A\sinh^{-1}p\ =\ \ln\left(\frac{x}{a}\right), \tag{8}\label{36.8}$$

or

$$x\ =\ ae^{A\phi}, \tag{9}\label{36.9}$$

where

$$\phi\ =\ \sinh^{-1}p. \tag{10}\label{36.10}$$

Equation ($\ref{36.9}$), with ($\ref{36.10}$), gives us the relation between $x$ and the slope, $p$. Note that $p$ and hence $f$ are negative, so that equation says that $x<a$.

Our next task will be to find a relation between $y$ and $p$ (or between $y$ and $\phi$).

From Equation ($\ref{36.10}$) we have

$$dy\ =\ \sinh\phi\ dx, \tag{11}\label{36.11}$$

and from Equation ($\ref{36.9}$) we have

$$dx\ =\ aAe^{A\phi}d\phi. \tag{12}\label{36.12}$$

From these we obtain the differential relation between $y$ and $\phi$:

$$dy\ =\ aAe^{A\phi}\sinh\phi d\phi, \tag{13}\label{36.13}$$

or

$$dy\ =\ \frac{1}{2}aA(e^{(A+1)\phi}\ -\ e^{(A-1)\phi})d\phi. \tag{14}\label{36.14}$$

Integrate this, with initial condition $\phi\ =\ 0$ when $y\ =\ 0$, to obtain

$$y\ =\ \frac{1}{2}aA\left(\frac{\left(\frac{x}{a}\right)^{1+1/A}}{A+1}-\frac{e^{(A-1)\phi}}{A-1}+\frac{2}{A^{2}-1}\right). \tag{15}\label{36.15}$$

Equation ($\ref{36.9}$) and ($\ref{36.15}$) are parametric equations to the path of the Dog, though it is easy to eliminate $\phi$ and write $y$ explicitly as a function of $x$:

$$y\ =\ \frac{1}{2}aA\left(\frac{e^{(A+1)\phi}}{A+1}-\frac{e^{(A-1)\phi}}{A-1}+\frac{2}{A^{2}-1}\right). \tag{16}\label{36.16}$$

The figure was drawn for $a=1,\ A=2,$ for which Equation ($\ref{36.16}$) reduces to

$$y\ =\ \frac{1}{3}[x^{\frac{1}{2}}(x-3)\ +\ 2]. \tag{17}\label{36.17}$$

The distance walked by the Man is found by putting $\phi=-\infty$ in Equation $\ref{36.15}$. Thus

$$y\ =\ \frac{aA}{A^{2}-1}, \tag{18}\label{36.18}$$

and the time taken is

$$t\ =\ \frac{aA}{v(A^{2}-1)} \tag{19}\label{36.19}$$

Exercise $\PageIndex{37}$

Let $l$ be the length of the string.

Exercise $\PageIndex{37a}$

Kinetic energy of the upper mass = $\frac{1}{2}(mr^{2})\omega^{2}\ +\frac{1}{2}m\dot{r}^{2}$.

Kinetic energy of the lower mass = $\frac{1}{2}m\dot{r}^{2}$

Potential energy of the lower mass = $m\text{g}(l-r)$.

Total energy of the system =

$$\frac{1}{2}(mr^{2})\omega^{2}\ + m\dot{r}^{2}\ -\ m\text{g}(l-r). \tag{1}\label{37a.1}$$

Initial total energy of the system =

$$\frac{1}{2}(ma^{2})\omega_{0}^{2}\ + m\dot{r}^{2}\ -\ m\text{g}(l-a). \tag{2}\label{37a.2}$$

Energy is conserved and therefore, by equating ($\ref{37a.1}$) and ($\ref{37a.2}$), we obtain

$$\dot{r}^{2}\ =\ \text{g}(a-r)\ +\ \frac{1}{2}a^{2}\omega_{0}^{2}\ -\ \frac{1}{2}r^{2}\omega^{2}. \tag{3}\label{37a.3}$$

Angular momentum is also conserved, and therefore

$$r^{2}\omega\ =\ a^{2}\omega_{0} \tag{4}\label{37a.4}$$

On elimination of $r$ between Equations ($\ref{37a.3}$) and ($\ref{37a.4}$) we obtain, after some algebra,

$$\frac{\dot{r}^{2}}{\text{g}a}\ =\ 1\ +\ \frac{a\omega_{0}^{2}}{2\text{g}}\left(1-\frac{\omega}{\omega_{0}}\right)\ -\sqrt{\frac{\omega_{0}}{\omega}}. \tag{5}\label{37a.5}$$

Exercise $\PageIndex{37b}$

If $a\omega_{0}^{2}\ =\ \text{g}$ it is trivial to show that

$$\frac{\dot{r}^{2}}{\text{g}a}\ =\ \frac{3}{2}\ -\frac{1}{2}\Omega\ -\frac{1}{\sqrt{\Omega }}. \tag{6}\label{37a.6}$$

Exercise $\PageIndex{37c}$

Algebra and calculus show that $\frac{3}{2}\ -\frac{1}{2}\Omega\ -\frac{1}{\sqrt{\Omega }}$ is negative for all positive $\Omega$ except for $\Omega\ =\ 1$, when it reaches a maximum value of zero.

Exercise $\PageIndex{37d}$

If $a\omega_{0}^{2}\ =\ 2\text{g}$ and $\Omega\ =\ \frac{\omega}{\omega_{0}}$ it is trivial to show that

$$\frac{\dot{r}^{2}}{\text{g}a}\ =\ 2\ -\ \Omega\ -\frac{1}{\sqrt{\Omega}} \tag{7}\label{37a.7}$$

Algebra and calculus show that $2\ -\ \Omega\ -\frac{1}{\sqrt{\Omega}}$ reaches a maximum value for $\Omega\ =\ \frac{\omega}{\omega_{0}}\ =\ \frac{1}{2^{\frac{2}{3}}}\ =\ 0.629\ 961$ at which time $\frac{\dot{r}^{2}}{(\text{g}a)}\ =\ 0.110\ 118$. That is, when $\dot{r}\ =\ 0.331\ 841\sqrt{\text{g}a}$ Equation ($\ref{37a.4}$) (conservation of angular momentum) shows that $r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ \sqrt[3]{2a}\ =\ 1.259\ 921a$.

Solution of $2\ -\ \Omega\ -\ \frac{1}{\sqrt{\Omega}}=0$ shows that the speed is zero when $\Omega\ =\ 1$ (the initial condition) and when (the equilibrium value). Equation ($\ref{37a.4}$) (conservation of angular momentum) shows that $r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ 1.618\ 034a$.

Exercise $\PageIndex{37e}$

If $a\omega_{0}^{2}\ =\ \frac{1}{2}\text{g}$ and $\Omega\ =\frac{\omega}{\omega_{0}}$ it is trivial to show that

$$\frac{\dot{r}^{2}}{\text{g}a}\ =\ \frac{5}{4}\ -\frac{1}{4}\Omega\ -\frac{1}{\sqrt{\Omega}} \tag{8}\label{37.8}$$

Algebra and calculus show that $\frac{5}{4}\ -\frac{1}{4}\Omega\ -\frac{1}{\sqrt{\Omega}}$ reaches a maximum value for $\Omega\ =\ \frac{\omega}{\omega_{0}}\ =\ 2^{\frac{2}{3}}\ =\ 1.587\ 401$ at which time $\frac{\dot{r}^{2}}{(\text{g}a)}=0.059449$. That is, when $\dot{r}\ =\ -0.243\ 822\sqrt{\text{g}a}$ Equation ($\ref{37a.4}$) (conservation of angular momentum) shows that $r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ \frac{a}{\sqrt[3]{2}}\ =\ 0.793\ 701a$.

Solution of $\frac{5}{4}\ -\frac{1}{4}\Omega\ -\frac{1}{\sqrt{\Omega}}$ shows that the speed is zero when $\Omega\ =\ 1$ (the initial condition) and when $\Omega\ =\ \frac{\omega}{\omega_{0}}\ =\ 2.438\ 447$ (the equilibrium value). Equation ($\ref{37a.4}$) (conservation of angular momentum) shows that $r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ 0.640\ 388a$.

How much further can we go with this question? By elimination of $r$ between Equations ($\ref{37a.3}$) and ($\ref{37a.4}$) we obtained a relation between $\dot{r}$ and $\omega$. By elimination of $\omega$ between Equations ($\ref{37a.3}$) and ($\ref{37a.4}$) we can get a relation between $\dot{r}$ and $r$. It will be of the form

$$\dot{r}\ =\ \sqrt{A\ -\ \text{g}r\ -\ \frac{B}{r^{2}}}, \tag{9}\label{37a.9}$$

where $A\ =\ \text{g}a\ +\ \frac{1}{2}a^{2}\omega_{0}^{2}$ and $B\ =\ a^{4}\omega_{0}^{4}$. If you can integrate this, you then get a relation between $r$ and $t$. I haven’t given much though as to whether you can get integrate Equation ($\ref{37a.9}$) analytically (if anyone manages it, please let me know), but at least a numerical integration will certainly be possible.

In another variation of the question, you can start with an equilibrium situation in which $a\omega_{0}^{2}\ =\ \text{g}$ and then add an extra mass $m$ (or $M$, if you want to make it more general) and then follow the motion from there. I leave that to you.

Exercise $\PageIndex{38}$

Let’s look at the rod from above when it is twisted in the horizontal plane through a small angle $\theta$.

Each of the points where the threads are attached to the rod is displaced horizontally through a distance $\frac{1}{2}D\theta$ (Since $\theta$ is small and $D\ <<L$ we can neglect the slight vertical rise in the position of the rod.) Each thread is now displaced from the vertical by an angle $\phi$ given by

The tension $T$ in each thread is $\frac{1}{2}m\text{g}\cos\phi$ which, to first order in $\phi$, is just $\frac{1}{2}m\text{g}$.

The horizontal component of each of these forces is $\frac{1}{2}m\text{g}\sin\phi$ which, to first order in $\phi$, is $\frac{1}{2}m\text{g}\phi$.

Therefore the rod experiences a restoring torque equal to $\frac{1}{2}m\text{g}D\phi$. But $\phi\ =\ \frac{\frac{1}{2}D\theta}{L}$ and therefore the restoring torque is $\frac{m\text{g}D^{2}\theta}{4L}$.

The equation of motion is therefore

$I\ddot{\theta}\ =\ -\frac{mgD^{2}}{4L}\theta$

and consequently the period $P$ of small oscillations is

$P\ =\ 2\pi\sqrt{\frac{4LI}{mgD^{2}}}\ =\ \frac{4\pi}{D}\sqrt{\frac{LI}{m\text{g}}}$.

If the rod is uniform and of length $2l$, its moment of inertia is $\frac{1}{3}ml^{2}$ and in that case the period of small oscillations is

$P\ =\ \frac{4\pi l}{D}\sqrt{\frac{L}{3\text{g}}}$.

There is no need to remind the reader to check the dimensions of these equations.

Exercise $\PageIndex{39}$

When the yo-yo has fallen through a distance $x$, it has lost potential energy $Mgh$, and it has gained translational kinetic energy $\frac{1}{2}mv^{2}$ and gained rotational kinetic energy $\frac{1}{2}I\omega^{2}$ where $\omega\ =\ \frac{v}{a}$. Therefore $Mgx\ =\ \frac{1}{2}Mv^{2}\ +\ \frac{1}{2}\ I\left(\frac{v}{a}\right)^{2}$ from which

$v^{2}\ =\ 2\ \cdot\ \frac{Ma^{2}\text{g}}{Ma^{2}\ +\ I}\ \cdot\ x$.

Thus, from the usual equations for constant linear acceleration, the acceleration is

$\frac{Ma^{2}}{Ma^{2}\ +\ I}\times\text{g}$.

The net downward force is $M\text{g}-P$ where $P$ is the tension in the string. This is equal to $M$ times the acceleration, from which we obtain

$P\ =\ \frac{1}{Ma^{2}+1}\times M\text{g}.$

Exercise $\PageIndex{40a}$

I have drawn four forces on the yo-yo. Its weight $M\text{g}$. The tension $P$ in the string. The normal reaction $N$ of the table on the yo-yo. And the frictional force $F$ of the table on the yo-yo. As long as the yo-yo is in contact with the table and there is no vertical acceleration, we must have $P\ +\ N\ =\ M\text{g}$.

Let us suppose that there is no slipping between the yo-yo and the table, so that the yo-yo rolls to the left. We note that there is a net force $F$ to the left, and a net counterclockwise torque about C equal to $Pa-Fb$. Thus the yo-yo accelerates to the left at a rate $\frac{F}{M}$ it and experiences a counterclockwise angular acceleration $(Pa-Fb)\frac{a}{I}$. If there is no slipping, these must be related by $\frac{F}{M}=b\times\frac{Pa-Fb}{I}$. Thus, if there is no slipping,

$$F\ =\ \left(\frac{Mab}{I\ +\ Mb^{2}}\right)P. \tag{1}\label{40a.1}$$

The linear acceleration to the left must be $\frac{F}{M}$, or

$$\underline{\underline{\frac{abP}{I+Mb^{2}}}} \tag{2}\label{40a.2}$$

_________________________

Alternative derivation:

There is a net counterclockwise torque about A equal to $Pa$. The moment of inertia with respect to A is $I\ +\ Mb^{2}$. Therefore there is an angular acceleration about A equal to $\frac{Pa}{I\ +\ Mb^{2}}$. Therefore the linear acceleration of C to the left is $\underline{\underline{\frac{abP}{I\ +\ Mb^{2}}}}$ and the frictional force $F$ is $M$ times this, or $F\ =\ \left(\frac{Mab}{I\ +\ Mb^{2}}\right)P$.

End of Alternative Derivation.

__________________________

However, if the yo-yo is just about to slip, $F\ =\ \mu N\ = \ \mu(M\text{g}-P)$. Upon substitution of this into Equation ($\ref{40a.1}$), we see that the yo-yo will just slip if

$$P\ =\ \frac{\mu M\text{g}(I\ +\ Mb^{2})}{\mu(I\ +\ Mb^{2})\ +\ Mab}. \tag{3}\label{40a.3}$$

That is, the yo-yo will roll to the left without slipping if

$$\underline{\underline{\mu\ >\ \frac{MabP}{(M\text{g}-P)(I+Mb^{2})}}} \tag{4}\label{40a.4}$$

Its linear acceleration is then given by Equation ($\ref{40a.2}$), namely

$$\underline{\underline{\frac{abP}{I+Mb^{2}}}} \tag{2}\label{40a.2b}$$

On the other hand, the yo-yo will rotate counterclockwise with no rolling if

$$\underline{\underline{\mu\ <\ \frac{MabP}{(M\text{g}-P)(I+Mb^{2})}}} \tag{5}\label{40a.5}$$

The sum of the counterclockwise moments of the forces about C is then $Pa-Fb$ where $F=\mu N=\mu(M\text{g}-P)$. The counterclockwise angular acceleration about C is

$$\frac{Pa-Fb}{I}\ =\ \underline{\underline{\frac{P(a-\mu b)-\mu M\text{g}}{I}}}. \tag{6}\label{40a.6}$$

Exercise $\PageIndex{40b}$

I have drawn the four forces on the yo-yo. Its weight $M\text{g}$. The normal reaction of the table on the yo-yo, which is also of magnitude $M\text{g}$. The tension $P$ in the string. And the frictional force $F$ of the table on the yo-yo.

At this point it may not be immediately obvious whether $F$ acts to the left or the right. For example, let us suppose that the coefficient of friction is zero. The force $P$ will result in a translation of the yo-yo to the right together with a clockwise rotation of the yo-yo. So, in which direction does the point A on the circumference of the yo-yo move - to the left or the right? It is hard to say, but one might suppose, qualitatively, that, if the moment of inertia is large, the induced rotation will be sluggish, so that A moves to the right. Whereas if $I$ is small, the induced rotation will be rapid, and A will move to the left in spite of the translational motion of the centre of mass to the right. From this we might conclude that, if $\mu\neq 0$, $F$ will act to the right if $I$ is small, and $F$ will act to the left if $I$ is large. The following analysis shows that this qualitative expectation is correct.centre of mass to the right. From this we might conclude that, if $\mu\neq 0$, $F$ will act to the right if $I$ is small, and $F$ will act to the left if $I$ is large. The following analysis shows that this qualitative expectation is correct.

(The reader might find some of the Problems in Section 8.2 of Chapter 8 to be helpful at this point, particularly Problem 2.5.)

For the time being, I have drawn $F$ as if acting towards the left.

Let us suppose there is no slipping and that the yo-yo rolls.

The sum of the clockwise moments of the forces about A is $P(a\ +\ b)$ and the moment of inertia about A is $I\ +\ Mb^{2}$. The yo-yo therefore undergoes an initial clockwise angular acceleration about A equal to $\frac{P(a\ +\ b)}{I+Mb^{2}}$ and, therefore (if there is no slipping), an initial linear acceleration of C to the right equal to

$$\underline{\underline{\frac{Pb(a\ +\ b)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40b.1}$$

The above linear acceleration must equal $\frac{(P-F)}{M}$ from which we obtain

$$F\ =\ \left(\frac{I-Mab}{I+Mb^{2}}\right)P \tag{2}\label{40b.2}$$

This shows that the frictional force $F$ acts to the left, as shown, if $I\ >\ Mab$ but if $I<Mab$ the frictional force $F$ acts to the right. This is in agreement with our qualitative expectations, namely that $F$ will act to the left if $I$ is large, and to the right if $I$ is small.

Let is consider three cases in turn: $I>Mab,\ I<Mab$ and $I=Mab$.

(i) $I>Mab$

In this case, $F$ acts to the left, as drawn. Provided $F<\mu M\text{g}$ there will be no slipping at A, and the yo-yo will roll to the right without slipping. On recalling Equation ($\ref{40b.2}$), we see that the yo-yo will roll to the right without slipping, with a linear acceleration given by Equation ($\ref{40b.1}$) if

$$\underline{\underline{\mu>\left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)}}. \tag{3}\label{40b.3}$$

The linear acceleration to the right is given by Equation ($\ref{40b.1}$), namely

$$\underline{\underline{\frac{Pb(a\ +\ b)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40b.1b}$$

However, if

$$\underline{\underline{\mu<\left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)}}. \tag{4}\label{40b.4}$$

slipping occurs at A. The frictional force is the no longer given by Equation ($\ref{40b.2}$), but is given by

$$F=\mu M\text{g}, \tag{5}\label{40b.5}$$

and it acts to the left.

(We are concerned in this problem with the initial motion. Once motion is underway, $\mu$ has to be replaced with the smaller coefficient of kinetic friction.)

The net force to the right is then $P-\mu M\text{g}$ so the linear acceleration of C to the right is

$$\underline{\underline{\frac{P-\mu M\text{g}}{M}}}. \tag{6}\label{40b.6}$$

Because of condition ($\ref{40b.4}$), this is necessarily positive.

The net clockwise moment of the forces about the centre of mass C is $Pa\ +\ \mu M\text{g}b$. The yo-yo therefore undergoes a clockwise angular acceleration about C ofcentre of mass C is $Pa\ +\ \mu M\text{g}b$. The yo-yo therefore undergoes a clockwise angular acceleration about C of

$$\underline{\underline{\frac{Pa\ +\ \mu M\text{g}b}{I}}}. \tag{7}\label{40b.7}$$

The linear acceleration to the right of the point A on the circumference of the yo-yo is $\frac{P\ -\ \mu M\text{g}}{M}\ -\ b\ \times\ \frac{Pa\ +\ \mu M\text{g}b}{I}$, and, because of condition ($\ref{40b.4}$), some algebra will show that this is necessarily positive, as expected.

(ii) $I<Mab$

In this case, $F$ acts to the right, and the linear acceleration is $\frac{(P\ +\ F)}{M}$. Provided that

$$\underline{\underline{\mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)}}, \tag{8}\label{40b.8}$$

the yo-yo will roll to the right with a linear acceleration given by Equation ($\ref{40b.1}$), namely

$$\underline{\underline{\frac{Pb(a\ +\ b)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40b.1c}$$

However, if

$$\underline{\underline{\mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)}}, \tag{9}\label{40b.9}$$

slipping occurs at A. The frictional force is then given by

$$F\ =\ \mu M\text{g}, \tag{10}\label{40b.10}$$

and it acts to the right.

The net force to the right is then $P\ +\ \mu M\text{g}$, so the linear acceleration to the right is

$$\underline{\underline{\frac{P\ +\ \mu M\text{g}}{M}}}. \tag{11}\label{40b.11}$$

The net clockwise moment of the forces about the centre of mass C is . The yo-yo therefore undergoes a clockwise angular acceleration about C ofcentre of mass C is . The yo-yo therefore undergoes a clockwise angular acceleration about C of

$$\underline{\underline{\frac{Pa\ -\ \mu M\text{g}b}{I}}}. \tag{12}\label{40b.12}$$

The linear acceleration to the left of the point A on the circumference of the yo-yo is $b\times\frac{Pa-\mu M\text{g}b}{I}-\frac{P+\mu M\text{g}}{M}$, and, because of condition ($\ref{40b.8}$), some algebra will show that this is necessarily positive, as expected.

$I=Mab$

In this case, $F$ is zero. Whatever the coefficient of friction, even zero, the yo-yo will undergo a linear acceleration $\frac{P}{M}$ to the right (Verify that this is consistent with Equation ($\ref{40b.1}$) ), and a clockwise angular acceleration about C equal to $\frac{Pa}{I}$. The linear acceleration to the right of the point A on the circumference of the yo-yo is

$\frac{P}{M}\ -b\times\frac{Pa}{I}$

which is zero. The initial linear velocity of the point A is therefore zero.

Exercise $\PageIndex{40c}$

I have drawn the four forces on the yo-yo. Its weight $M\text{g}$. The normal reaction of the table on the yo-yo, which is also of magnitude $M\text{g}$. The tension $P$ in the string. And the frictional force $F$ of the table on the yo-yo. On this occasion (unlike in Problem 40 (b)) there is no question about the direction of $F$, which is towards the left.

Let us suppose there is no slipping.

The sum of the clockwise moments of the forces about A is $\frac{P(b-a)}{I\ +\ Mb^{2}}$ and the moment of inertia about A is $I\ +\ Mb^{2}$. The yo-yo therefore undergoes an initial clockwise angular acceleration about A equal to $\frac{P(b-a)}{I\ +\ Mb^{2}}$ and therefore (if there is no slipping) an initial linear acceleration to the right equal to

$$\underline{\underline{\frac{Pb(b-a)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40c.1}$$

Additional string therefore becomes wrapped around the axle. (Yes, it really does! I tried it!)

The above linear acceleration must equal $\frac{(P-F)}{M}$ from which we obtain

$$F\ =\ \left(\frac{I\ +\ Mab}{I\ +\ Mb^{2}}\right)P. \tag{2}\label{40c.2}$$

Provided $F < \mu Mg$,there will be no slipping at A, and the yo-yo will roll to the right without slipping. Thus the yo-yo will roll to the right without slipping, with a linear acceleration given by equation (1) if

$$\underline{\mu> \frac{\left( \frac{I+Mab}{I+Mb^2}\right)}{\left( \frac{P}{Mg}\right)}.} \tag{2}\label{40c.3}$$

$$\underline{\mu < \frac{\left( \frac{I+Mab}{I+Mb^2}\right)}{\left( \frac{P}{Mg}\right)}}, \label{40c.4}$$

$$F = \mu Mg, \tag{2}\label{40c.5}$$

$$\underline{\frac{P- \mu Mg}{M}}.\label{40c.6}$$

$$\underline{\frac{Pa- \mu Mgb}{I}} \label{40c.7}$$

Exercise $\PageIndex{40d}$

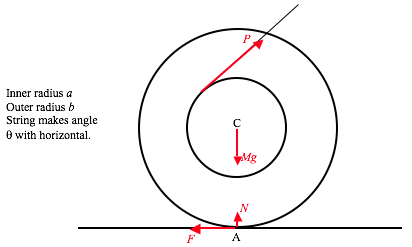
$$\frac{Pb(a + b \cos \theta}{I+Mb^2} \tag{1}\label{40d.1}$$

$$F = \left(\frac{I \cos \theta - Mab}{I+Mb^2}\right)P. \tag{2}\label{40d.2}$$

Exercise $\PageIndex{40E}$

$$\frac{P(b \cos \theta - a)}{I + Mb^2}. \tag{1}\label{40e.1}$$

$$\frac{P(b-\cos \theta - a)}{I + Mb^2}. \tag{2}\label{40e.2}$$

$$F = \left(\frac{I \cos \theta + Mab}{I + Mb^2}\right)P, \tag{3}\label{40e.3}$$

$$\frac{P(a-b\cos\theta}{I+Mb^2}. \tag{4}\label{40e.4}$$

$$\frac{Pb(a-b\cos\theta}{I+Mb^2} \tag{5}\label{40e.5}$$

$$F = \left(\frac{I\cos \theta + Mab}{I + Mb^2}\right)P, } \label{40e.6}$$

Exercise $\PageIndex{41}$

$3 m \overline{x} = 2 ma + m \times \frac{4}{3} a$

$3 m \overline{y} = 2 m \times \frac{1}{2}a + m \times{4}{3} a.$

$\overline{x} = \frac{10}{9} a \qquad \overline{y} = \frac{7}{9}a.$

$\frac{1}{2}\begin{bmatrix}x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 &1 \end{bmatrix}.$

$\frac{1}{3}(2m)(\frac{1}{2} a)^2 = \frac{1}{6} ma^2.$

$= \frac{1}{3}(2m)a^2 = \frac{2}{3} ma^2.$

= 0.

$A_{rect} = \frac{1}{6} ma^2 + 2m(\frac{5}{18}a)^2 = \frac{28}{81}ma^2.$

$B_{rect} = \frac{2}{3} ma^2 + 2m(\frac{1}{9} a)^2 = \frac{65}{81} ma^2$

$H_{rect} = 0 + 2m(\frac{1}{9}a)(\frac{5}{18}a) = \frac{5}{81} ma^2.$

$= \frac{1}{6} ma^2 - m(\frac{1}{3}a)^2 = \frac{1}{18}ma^2.$

$= \frac{1}{6} (m)(2a)^2 - m( \frac{1}{3} \times 2a)^2 = \frac{2}{9}ma^2.$

$+ \frac{1}{36}m(2a)(a) = +\frac{1}{18} ma^2.$

$A_{tria} = \frac{1}{18} ma^2 + m(\frac{5}{8} a)^2 = \frac{59}{162}ma^2.$

$B_{tria} = \frac{2}{9} ma^2 + m(\frac{2}{9} a)^2 = \frac{22}{81}ma^2.$

$H_{tria} = \frac{1}{18}ma^2 + m(-\frac{2}{9}a)(-\frac{5}{9}a) =\frac{29}{162}ma^2.$

$A = \frac{26}{81}ma^2 + \frac{59}{162}ma^2 = \frac{37}{51}ma^2.$

$B = \frac{56}{81}{ma^2+\frac{22}{81}}ma^2 = \frac{26}{27}ma^2.$

$H = \frac{5}{81}ma^2+\frac{29}{162}m= \frac{13}{54}ma^2.$

$\theta =$ 30º.009 180 and 120º.009 180

$A \cos^2 \theta - 2 H \sin \theta \cos \theta + b \sin^2 \theta.$

$A_0$ = 0.546142ma² , $B_0$= 1.102006ma².

Exercise $\PageIndex{42}$

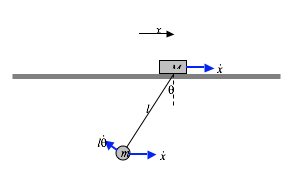
$T = \frac{1}{2} Mx^2 + \frac{1}{2}m(\dot{x}^2 + l^2 \dot{\theta}^2 +2l\dot{\theta}\dot{x} \cos \theta$

$V = \text{constant} - mgl \cos \theta.$

$(M+ m)\ddot{x} + ml(\ddot{\theta} \cos \theta - \dot{\theta}^2 \sin \theta) = 0,$

$l \ddot{\theta} + \ddot{x} + g \theta = 0.$

$\ddot{\theta} = - \frac{(M+m)g}{Ml}\theta$

$\underline{\underline{2 \pi = \sqrt{\frac{Ml}{M+m}g}}}.$

Exercise $\PageIndex{43}$

$\frac{1}{k} \frac{dr}{d \alpha} = - \frac{1}{2} \sin \alpha \sin 2 \alpha + 2 \cos^2 \frac{1}{2} \alpha \cos 2 \alpha$

$= - \sin^2 \alpha \cos \alpha + (1 + \cos \alpha) (2 \cos^2 \alpha -1) = 0.$

$\underline{\underline{3c^2 + 2c^2 - 2c - 1 = 0}}$

Exercise $\PageIndex{44}$

The condition for stability, from Chapter 16 Section 16.9, Equation 16.9.5 is that

$\frac{Ak^{2}}{V}>\text{HC}$.

$k^{2}$ for a filled circle of radius $a$ is $\frac{1}{4}a^{2}$. If the length of the cylinder is $l$, the volume immersed is $Asl$, so the left hand side of the inequality is $\frac{a^{2}}{4sl}$.

The depth of the centre of mass is $l(s-\frac{1}{2})$ and the depth of the centre of buoyancy is $\frac{1}{2}ls$, so that $\text{HC}\ =\ \frac{1}{2}l(1-s)$. The condition for stability is, then, $\frac{a^{2}}{4sl}>\frac{1}{2}l(1-s)$.

With $L\ =\frac{l}{(2a)}$, this gives, for the condition for stability,

$\underline{\underline{L\ <\ \frac{1}{\sqrt{8s(1-s)}}}}$

This function is least for $s=\frac{1}{2},\ L\ <\ \frac{1}{\sqrt{2}}=0.707$. For any length less than this, the system is stable for any density. With $L=1$, the inequality can be written $8s^{2}-8s+1>0$, so that $s$ must be less than 0.146 or greater than 0.854.

Exercise $\PageIndex{45}$

Before doing the problem, let’s just have a look at the “interesting” property of a (4, 5, 6) triangle

Calculate $A$ by the cosine rule: $16\ =\ 25\ +\ 36\ -60\cos A$, hence $\cos A\ =\ \frac{3}{4}$.

Calculate $C$ by the cosine rule: $36\ =\ 16\ +\ 25\ -40\cos C$, hence $\cos C\ =\ \frac{1}{8}$.

But $\cos 2A\ =\ 2\cos^{2}\ A\ -1\ =\frac{1}{8}$. Therefore $C\ =\ 2A$.

The external angle at B is $3A$.

The angles are $A\ =\ 41^{\circ}.4096 \quad C\ =\ 82^{\circ}.8192 \quad B\ =\ 55^{\circ}.7711 \quad \left(\cos B=\frac{9}{16}\right)$

Supplement of $B\ =\ 124^{\circ}.2289$

It is not the case that a triangle with one angle equal to twice another one is necessarily a (4, 5, 6) triangle.

After that diversion, let’s move on to the given problem - except that we’ll generalize it to make the length of the rod $2l$, and the lengths of the strings $a$ and $b$.

The only physics involved is to recall that, if three coplanar forces are in equilibrium, they must be concurrent at a point - in this case the point C. This means that C must be vertically above the mid-point of the rod.

After that, there is no more physics; the rest is “just” geometry. All we have to do is to find $\theta$ in terms of $a$ and $b$.

If C is to be directly above the mid-point, then AN = MB. That is:

$b\cos(A+\theta)\ =\ a\cos(B-\theta)$.

This quickly results in

$\tan\theta=\frac{b\cos A\ -\ a\cos B}{b\sin A\ +\ a\sin B}$.

In our particular example, $\frac{a}{b}\ =\ \frac{4}{5}\ =\ 0.8,\ B\ =\ 180^{\circ}\ -\ 3A$, and $A\ =\ 41^{\circ}.4096$.

Thus

$\tan\theta\ =\ \frac{\cos A\ +\ 0.8\cos3A}{\sin A\ +\ 0.8\sin3A}$,

and

$\underline{\theta\ =\ 12^{\circ}.78}$

If the weight of the rod is $m\text{g}$, I’ll leave it to you to work out the tensions in the strings.

Exercise $\PageIndex{46}$

The only physics involved is to recall that, if three coplanar forces are in equilibrium, they must be concurrent at a point - in this case the point C. This means that C must be vertically above the mid-point. Also, since the planes are smooth, the forces at A and B are perpendicular to the planes.

The rest is geometry - almost the same as in Problem 45, except that in this problem we are given the angles $\alpha$ and $\beta$ rather than the lengths $a$ and $b$. Start by convincing yourself that the two angles at C are indeed $\alpha$ and $\beta$, as marked. Now all that is required is to express $\theta$ in terms of $\alpha$ and $\beta$.

Since the mid-point of the rod must be vertically below C, we must have AN = MB. That is:

$b \sin \alpha = a \sin \beta$.

By the Sine Rule, $\frac{b}{a} = \frac{\sin B}{\sin A}$, so that $\sin \alpha \sin B = \sin \beta \sin A$

But $A = 90$° $- \alpha + \theta$ and $B = 90$° $-\beta - \theta$, so

$\sin \alpha = \cos(\beta - \theta) = \sin\beta\cos(\alpha + \theta)$,

which quickly yields $\underline{\underline{\tan \theta = \frac{1}{2}(\cot \alpha - \cot \beta)}}$. In our particular example, this is $\tan \theta = \frac{1}{2}(\sqrt{3} - 1), \underline{\underline{\theta = }}$20.1°. If you wish, you could work out the forces at A and B in terms of the weight of the rod.

Exercise $\PageIndex{47}$

I have drawn above the three forces on the rod. The forces at the ends of the rod each make an angle $\lambda$ to the normal to the surface, where $\tan \lambda = \mu$, and the three coplanar forces, being in static equilibrium, are concurrent at a point. I have also introduced the angle $\phi$, given by $\cos \phi = l/a$. All we have to do is to find $\theta$ in terms of $\lambda$ and $\phi$ - that is to say, in terms of $\mu$ and $l/a$

Fortunately I found the following formula for a triangle in an old geometry book:

$\cot \gamma = \frac{1}{2}(\cos \alpha - \cot \beta)$

I’ll leave you to see if you can derive it. The book actually gave a formula for a more general case in which the base of the triangle isn’t divided equally. For the case

the formula is $(1+x) \cot \gamma = \cot \alpha - x \cot \beta$.

You can use this in various problems in geometric optics, where you are trying to find relations between object distance, image distance and radius of curvature or focal length. However, for this problem, we need only the simpler formula, where the base of the triangle is equally divided.

On applying the simpler formula to our present problem we obtain

$\underline{\underline{\tan \theta = \frac{1}{2}[\cot ( \phi - \lambda) - \cot( \phi + \lambda)]}},$

and the problem is solved.

Below, I illustrate some examples. Going from left to right we have short $l/a=0.2$, medium $l/a=0.4$, long $l/a= 0.6$ rod. Going from top to bottom we have a slippery $\mu = 0.5$, a medium $/mu = 1.0$, and a sticky $/mu = 1.5$ surface.

Inside each drawing, I tabulate

$l/a$

$/mu$

$\theta$°

The long $(l / a =0.6)$ rod will rest vertically for any $/mu > 1.33$. But, while it will not slip, the equilibrium is no longer stable, and the rod will tip after an infinitesimal counterclockwise displacement.