Prólogo
( \newcommand{\kernel}{\mathrm{null}\,}\)
Dos enfoques filosóficos dramáticamente diferentes de la ciencia se desarrollaron en el campo de la mecánica clásica durante losth siglos 17th - 18. Este periodo de tiempo coincidió con la Era de la Ilustración en Europa durante la cual se produjeron notables desarrollos intelectuales y filosóficos. Esta fue una época en la que tanto los argumentos filosóficos como los causales eran igualmente aceptables en la ciencia, en contraste con la convención actual donde parece haber un acuerdo tácito para desincentivar el uso de argumentos filosóficos en la ciencia.
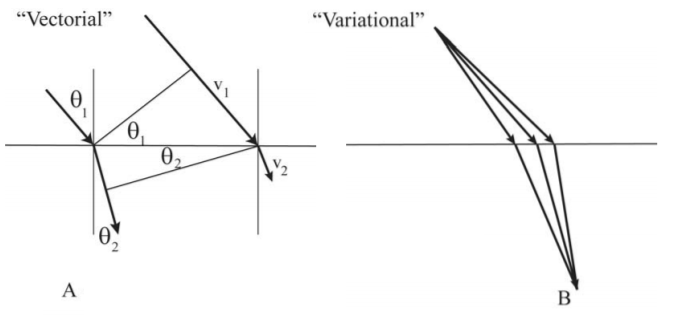
F igure1: Representación vectorial y variacional de la Ley de Snell para la refracción de la luz.
Ley de Snell
La génesis de dos enfoques filosóficos contrastantes de la ciencia se relaciona con los primeros estudios sobre la reflexión y refracción de la luz. La velocidad de la luz en un medio de índice de refracciónn es igualv=cn. Así, un haz de luz incidente en ánguloθ1 con la normal de una interfaz plana entre el medio 1 y el medio 2 se refracta en un ánguloθ2 en el medio 2 donde los ángulos están relacionados por la Ley de Snell.
\ [\ label {eq:Ley de Snell}\ tag {Ley de Snell}
\ frac {\ sin\ theta_1} {\ sin\ theta_2} =\ frac {v_1} {v_2} =\ frac {n_2} {n_1}\]
Ibn Sahl de Bagdad (984) describió por primera vez la refracción de la luz, mientras que Snell (1621) derivó matemáticamente su ley. Ambos científicos utilizaron el “enfoque vectorial” donde se considera que la velocidad de la luzv es un vector apuntando en la dirección de propagación.
Principio de Fermat
El principio de Fermat de menor tiempo (1657), que se basa en la obra de Héroe de Alejandría (~ 60) e Ibn al-Haytham (1021), establece que “la luz viaja entre dos puntos dados a lo largo del camino del menor tiempo”, donde el tiempoτ de tránsito de un haz de luz entre dos ubicacionesA yB en un medio con índice de refracción dependiente de la posiciónn(s) dado por
\ [\ tag {Principio de Fermat}
\ tau=\ int_ {T_a} ^ {T_b} dt =\ frac {1} {c}\ int_a^bn (s) ds
\ label {EQ:Principio de Fermat}\]
El Principio de Fermat lleva a la derivación de la Ley de Snell.
Filosóficamente, la física subyacente a las derivaciones vectoriales contrastantes y del Principio de Fermat de la Ley de Snell son dramáticamente diferentes. El enfoque vectorial se basa en las relaciones diferenciales entre los vectores de velocidad en los dos medios, mientras que el enfoque variacional de Fermat se basa en el hecho de que la luz selecciona preferentemente una trayectoria para la cual la integral del tiempo de tránsito entre la ubicación inicialA y la final la ubicaciónB se minimiza. Es decir, el primer enfoque se basa en la “mecánica vectorial” mientras que el enfoque de Fermat se basa en principios variacionales en que el camino entre las ubicaciones inicial y final es variado para encontrar el camino que minimiza el tiempo de tránsito. La enunciación de principios variacionales de Fermat en física jugó un papel clave en el desarrollo histórico, y posterior explotación, del principio de menor acción en las formulaciones analíticas de la mecánica clásica como se discute a continuación.
Mecánica Newtoniana
El impulso y la fuerza son vectores que subyacen a la formulación newtoniana de la mecánica clásica. El monumental tratado de Newton, titulado “Philosophiae Naturalis Principia Mathematica”, publicado en 1687, estableció sus tres leyes universales del movimiento, la teoría universal de la gravitación, la derivación de las tres leyes del movimiento planetario de Kepler y el desarrollo del cálculo. Las tres leyes universales del movimiento de Newton proporcionan el enfoque más intuitivo de la mecánica clásica en el sentido de que se basan en cantidades vectoriales como el impulso, y la tasa de cambio de impulso, que están relacionadas con la fuerza. Ecuación del movimiento de Newton
F=dpdt
es una relación diferencial vectorial entre las fuerzas instantáneas y la tasa de cambio de momento, o aceleración instantánea equivalente, todas las cuales son cantidades vectoriales. El momento y la fuerza son fáciles de visualizar, y tanto la causa como el efecto están incrustados en la mecánica newtoniana. Por lo tanto, si se conocen todas las fuerzas, incluidas las fuerzas de restricción, que actúan sobre el sistema, entonces el movimiento es solucionable para dos sistemas corporales. Las matemáticas para manejar el enfoque de la “mecánica vectorial” de Newton a la mecánica clásica están bien establecidas.
Mecánica Analítica
Los principios variacionales se aplican a muchos aspectos de nuestra vida diaria. Los ejemplos típicos incluyen; seleccionar el compromiso óptimo en calidad y costo al comprar, seleccionar la ruta más rápida para viajar de casa al trabajo, o seleccionar el compromiso óptimo para satisfacer los deseos dispares de las personas que forman una familia. Los principios variacionales subyacen a la formulación analítica de la mecánica. Es sorprendente que las leyes de la naturaleza sean congruentes con principios variacionales que involucran el principio de menor acción. Minimizar la integral de acción condujo al desarrollo del campo matemático del cálculo variacional, más los enfoques variacionales analíticos de la mecánica clásica, por Euler, Lagrange, Hamilton y Jacobi.
Leibniz, quien era contemporáneo de Newton, introdujo métodos basados en una cantidad llamada “vis viva”, que en latín significa “fuerza viva” y equivale al doble de la energía cinética. Leibniz creía en la filosofía de que Dios creó un mundo perfecto donde la naturaleza sería ahorrativa en todas sus manifestaciones. En 1707, Leibniz propuso que el camino óptimo se basa en minimizar la integral de tiempo del vis viva, lo que equivale a la integral de acción de la mecánica lagrangia/hamiltoniana. En 1744 Euler derivó el resultado de Leibniz utilizando conceptos variacionales mientras Maupertuis reafirmó el resultado de Leibniz con base en argumentos teleológicos. El desarrollo de la mecánica lagrangiana culminó con la publicación de 1788 del monumental tratado de Lagrange titulado “Mécanique Analytique”. Lagrange utilizó el Principio de d'Alembert para derivar la mecánica lagrangiana proporcionando un poderoso enfoque analítico para determinar la magnitud y dirección de las trayectorias óptimas, más las fuerzas asociadas.
La culminación del desarrollo de la mecánica analítica ocurrió en 1834 cuando Hamilton propuso su Principio de Acción Menor, así como el desarrollo de la mecánica hamiltoniana que es el principal enfoque variacional en la ciencia. El concepto de menor acción de Hamilton se define como la integral de tiempo del lagrangiano. El principio de acción de Hamilton (1834) minimiza la integral de acciónS definida por
S=∫BAL(q,˙q,t)dt
En la forma más simple, el lagrangianoL(q,˙q,t) equivale a la diferencia entre la energía cinéticaT y la energía potencialU. El principio de menor acción de Hamilton subyace a la mecánica lagrangiana. Este lagrangiano es una función de coordenadasn generalizadasqi más sus velocidades correspondientes˙qi. Hamilton también desarrolló el enfoque variacional premier, llamado mecánica hamiltoniana, que se basa en la hamiltonianaH(q,p,t) que es una función de la posiciónn fundamentalqi más laspi variables de impulso conjugadas. En 1843 Jacobi proporcionó el marco matemático requerido para explotar plenamente el poder de la mecánica hamiltoniana. Tenga en cuenta que la integral lagrangiana, hamiltoniana y de acción, todas son cantidades escalares lo que simplifica la derivación de las ecuaciones de movimiento en comparación con el cálculo vectorial utilizado por la mecánica newtoniana.
La figura2 presenta una hoja de ruta filosófica que ilustra la jerarquía de enfoques filosóficos basados en el Principio de Acción de Hamilton, que están disponibles para derivar las ecuaciones de movimiento de un sistema. El principalStage1 utiliza la acción funcional de Hamilton,S=∫tftiL(q,˙q,t)dt para derivar los funcionales lagrangianos y hamiltonianos que proporcionan el nivel de comprensión más fundamental y sofisticado. Stage1implica especificar todos los grados activos de libertad, así como las interacciones involucradas. Stage2utiliza los funcionales lagrangianos o hamiltonianos, derivados enStage1, con el fin de derivar las ecuaciones de movimiento para el sistema de interés. Stage3luego usa estas ecuaciones derivadas de movimiento para resolver el movimiento del sistema sujeto a un conjunto dado de condiciones iniciales de contorno. Tenga en cuenta que Lagrange primero derivó la mecánica lagrangiana basada en el Principio de d' Alembert, mientras que las Leyes del Movimiento de Newton especifican las ecuaciones de movimiento utilizadas en la mecánica newtoniana.
El enfoque analítico de la mecánica clásica parecía contradictorio con el tratamiento vectorial intuitivo de Newton de la fuerza y el impulso. Existe una diferencia dramática en la filosofía entre las ecuaciones vector-diferencial de movimiento derivadas de la mecánica newtoniana, que relacionan la fuerza instantánea con la aceleración instantánea correspondiente, y la mecánica analítica, donde minimizar la integral de acción escalar involucra integrales sobre el espacio y el tiempo entre estados iniciales y finales especificados. La mecánica analítica utiliza principios variacionales para determinar la trayectoria óptima, a partir de un continuo de posibilidades tentativas, al requerir que la trayectoria óptima minimice la integral de acción entre las condiciones iniciales y finales especificadas.
Inicialmente hubo considerable prejuicio y oposición filosófica al uso del enfoque de principios variacionales que se basa en el supuesto de que la naturaleza sigue los principios de la economía. El enfoque variacional no es intuitivo, por lo que se consideró especulativo y “metafísico”, pero se toleró como una herramienta eficiente para explotar la mecánica clásica. Esta oposición a los principios variacionales subyacentes a la mecánica analítica, retrasó la apreciación completa del enfoque variacional hasta principios delth siglo XX. Como consecuencia, la formulación newtoniana intuitiva reinó suprema en la mecánica clásica durante más de dos siglos, a pesar de que las notables capacidades de resolución de problemas de la mecánica analítica fueron reconocidas y explotadas tras el desarrollo de la mecánica analítica por Lagrange.
La plena significación y superioridad de las formulaciones variacionales analíticas de la mecánica clásica se reconocieron y aceptaron tras el desarrollo de la Teoría Especial de la Relatividad en 1905. La Teoría de la Relatividad requiere que las leyes de la naturaleza sean invariantes al marco de referencia. Esto no se satisface con la formulación newtoniana de la mecánica que asume un marco absoluto de referencia y una separación entre el espacio y el tiempo. En contraste, las formulaciones lagrangianas y hamiltonianas del principio de menor acción siguen siendo válidas en la Teoría de la Relatividad, si la lagrangiana está escrita en una forma relativisticamente-invariante en el espacio-tiempo. La invarianza completa del enfoque variacional para coordinar marcos es precisamente el formalismo necesario para manejar la mecánica relativista.
La mecánica hamiltoniana, que se expresa en términos de las variables conjugadas(q,p), relaciona la mecánica clásica directamente con la física subyacente de la mecánica cuántica y la teoría cuántica de campos. Como consecuencia, la oposición filosófica a la explotación de los principios variacionales ya no existe, y la mecánica hamiltoniana se ha convertido en la formulación preeminente de la física moderna. El lector es libre de sacar sus propias conclusiones respecto a la cuestión filosófica “¿es el principio de economía una ley fundamental de la mecánica clásica, o es una consecuencia fortuita de las leyes fundamentales de la naturaleza?”
Desde finales del siglo XVII, hasta los albores de la física moderna a principios del siglo XX, la mecánica clásica siguió siendo una fuerza impulsora primaria en el desarrollo de la física. La mecánica clásica abarca una gama inusualmente amplia de temas que abarcan el movimiento de cuerpos astronómicos macroscópicos hasta partículas microscópicas en física nuclear y de partículas, a velocidades que van desde cero hasta cerca de la velocidad de la luz, desde sistemas unicorporales hasta sistemas estadísticos de muchos cuerpos, además de tener extensiones a la mecánica cuántica. La introducción de la Teoría Especial de la Relatividad en 1905, y la Teoría General de la Relatividad en 1916, requirieron modificaciones en la mecánica clásica para las velocidades relativistas, y puede considerarse como una teoría extendida de la mecánica clásica. Desde la década de 1920, la física cuántica ha remplazado a la mecánica clásica en el dominio microscópico. Aunque la física cuántica ha jugado el papel principal en el desarrollo de la física durante gran parte del siglo pasado, la mecánica clásica sigue siendo un campo vibrante de la física que recientemente ha llevado a desarrollos emocionantes asociados con los sistemas no lineales y la teoría del caos. Esto ha generado nuevas ramas de la física y las matemáticas, además de cambiar nuestra noción de causalidad.
Goles
El objetivo principal de este libro es presentar al lector los poderosos enfoques de principios variacionales que juegan un papel tan fundamental en la mecánica clásica y en muchas otras ramas de la ciencia e ingeniería modernas. Este libro enfatiza la belleza intelectual de estos notables desarrollos, además de enfatizar las implicaciones filosóficas que han tenido un tremendo impacto en la ciencia moderna. Un objetivo secundario es aplicar principios variacionales para resolver aplicaciones avanzadas en la mecánica clásica con el fin de introducir muchas técnicas matemáticas sofisticadas y poderosas que subyacen a gran parte de la física moderna.
Este libro comienza con una revisión de la mecánica newtoniana más las soluciones de las ecuaciones de movimiento correspondientes. A esto le sigue una introducción a la mecánica lagrangiana, basada en el Principio de d'Alembert, con el fin de desarrollar familiaridad en la aplicación de principios variacionales a la mecánica clásica. Esto lleva a la introducción del Principio de Acción de Hamilton, más fundamental, más la mecánica hamiltoniana, para ilustrar el poder que proporciona la explotación de la jerarquía completa de etapas disponibles para aplicar principios variacionales a la mecánica clásica. Finalmente, el libro ilustra cómo se aprovecharon los principios variacionales en la mecánica clásica durante el desarrollo tanto de la mecánica relativisitica como de la física cuántica. Las conexiones y aplicaciones de la mecánica clásica a la física moderna, se enfatizan a lo largo del libro en un esfuerzo por abarcar el abismo que divide la formulación vector-diferencial newtoniana, y la formulación variacional integral, de la mecánica clásica. Este abismo es especialmente aplicable a la mecánica cuántica que se basa completamente en principios variacionales. Tenga en cuenta que los principios variacionales, desarrollados en el campo de la mecánica clásica, ahora se utilizan en una amplia y diversa gama de campos fuera de la física, incluyendo la economía, la meteorología, la ingeniería y la computación.
Este estudio de la mecánica clásica implica escalar una vasta montaña de conocimiento, y el camino hacia la cima conduce a teorías elegantes y hermosas que subyacen a gran parte de la física moderna. Este libro explota principios variacionales aplicados a cuatro temas principales de la mecánica clásica para ilustrar el poder y la importancia de los principios variacionales en la física. Estar tan cerca de la cumbre brinda la oportunidad de dar algunos pasos adicionales más allá del programa de estudios de introducción a la mecánica clásica normal para vislumbrar la emocionante física que se encuentra en la cumbre. Esta nueva física incluye temas como la mecánica cuántica, relativista y estadística.

