1: Dualidad onda-corpuscular de fotones y partículas masivas

Objetivos

En este capítulo se revisan los principales resultados experimentales que muestran el comportamiento dual de la luz. En la última sección se introduce el concepto de amplitud de probabilidad jugando un papel clave en la mecánica cuántica

Prerrequisitos

Elementos de la mecánica clásica, interferencia de la luz. Elementos de cálculo y teoría de probabilidad. El concepto de distribución de probabilidad.

El experimento de doble rendija con luz

La naturaleza de la luz, ya sea que consista en corpúsculos o sea una ola de un medio no identificado, llamado éter, intrigó a los científicos durante mucho tiempo antes de principios del siglo XX, y hubo una disputa de larga data entre los dos puntos de vista. Una solución aparentemente final llegó junto con los numerosos experimentos de interferencia a principios del siglo XIX realizados por Thomas Young, Augustine Fresnel y otros, que habían mostrado la naturaleza ondulada de la luz. Aquí presentamos el experimento de doble rendija de Young. Es interesante que unos 100 años después en 1909 Geoffrey Taylor repitió el experimento con un haz muy débil que resultó en las mismas franjas después de un tiempo suficientemente largo.

Figura 1.1: El experimento de doble rendija de Young. Las ondas de luz secundarias que emergen de las dos ranuras muestran franjas de interferencia en la pantalla a lo largo de la dirección x. Esto fue considerado durante mucho tiempo como la prueba de la naturaleza ondulada de la luz.

La hipótesis de los fotones

Resultó sin embargo, que la naturaleza es más complicada que la imaginación del hombre simple. El primer paso hacia una comprensión más profunda de lo que es la luz lo hizo Max Planck en 1900. Para explicar correctamente la distribución espectral de la radiación emitida por un cuerpo caliente como el sol, o una pieza calentada de hierro, tuvo que asumir que las ondas de luz que emergían del cuerpo absorbieron energía de él en cuantos. La menor cantidad de cuántica está determinada por la frecuencia\( \nu \) de la luz emitida y una constante universal h para que un solo cuántico tenga

\( \varepsilon=h \nu \)(1.1)

energía, donde el requisito de estar de acuerdo con las observaciones experimentales determinó el valor de

\( h=6.63 \times 10^{-34} \mathrm{Js} \)(1.2)

llamada la constante de Planck. Este es un valor extremadamente pequeño por lo tanto, incluso para la luz visible la energía de un solo cuántico es solo del orden de 10 ^{− 19} J, es por eso que no observamos esta propiedad granular de la luz.

Figura 1.2: Dibujo esquemático que demuestra el efecto fotoeléctrico. http://hyperphysics.phy-astr.gsu.edu/hbase/mod1.html

El siguiente paso fundamental fue cuando A. Einstein extendió las ideas de Planck a la explicación del efecto fotoeléctrico descubierto por Hallwachs y Stoletov y estudiado en detalle por P. Lenard y Herz. Si la luz cae sobre la superficie de un metal, ésta se carga positivamente. La razón de esto es que los electrones, es decir, partículas cargadas negativamente llamadas fotoelectrones se emiten desde la superficie del metal. Sobre los detalles de este fenómeno nos referimos aquí a cursos de física experimental. Las observaciones fueron explicadas por Einstein, por el supuesto de que los electrones en el metal absorben la energía del campo de luz en cuantos. Siguiendo la idea de Planck, Einstein asumió que la energía de un solo cuántico de luz es

\( \varepsilon=h \nu \)(1.3)

donde\( \nu \) está la frecuencia de la luz, h es la constante de Planck. Una notación de uso frecuente es

\( \hbar=\frac{h}{2 \pi} \)(1.4)

y con la frecuencia angular\( \omega=2 \pi \nu \) podemos escribir la relación de Einstein como

ε = ω (1.5)

que se utiliza más a menudo es la física teórica. El cuántico energético de la luz obtuvo el nombre de fotón. La energía cinética de los electrones emitidos viene dada por la siguiente ecuación:

\( E_{k i n}=h \nu-W_{a} \)(1.6)

donde W _a — llamada “función de trabajo” — es la energía necesaria para extraer el electrón del metal, que es característico del metal. Si\( h \nu \) es menor que W _a, no hay emisión de electrones. Para los metales alcalinos Na, Cs incluso la luz visible muestra el efecto, mientras que para la mayoría de los metales la frecuencia umbral determinada por\( h \nu_{t}=W_{a} \) cae en la región ultravioleta.

Los supuestos de Einstein fueron probados exactamente más tarde por experimentos de Millikan en el efecto fotoeléctrico. El valor de E _kin puede ser determinado por la contratensión U ₀ dada al electrodo que registra los electrones. El valor de q ₀ U ₀ —donde q ₀ es la carga del electrón— que detiene los electrones da W _a. La ecuación (1.6) es la ecuación fotoeléctrica de Einstein, que se puede probar trazando U ₀ versus la frecuencia de la luz\( \nu \).

Figura 1.3: Trazando la contratensión U ₀ frente a la frecuencia de la luz\( \nu \).

Animación

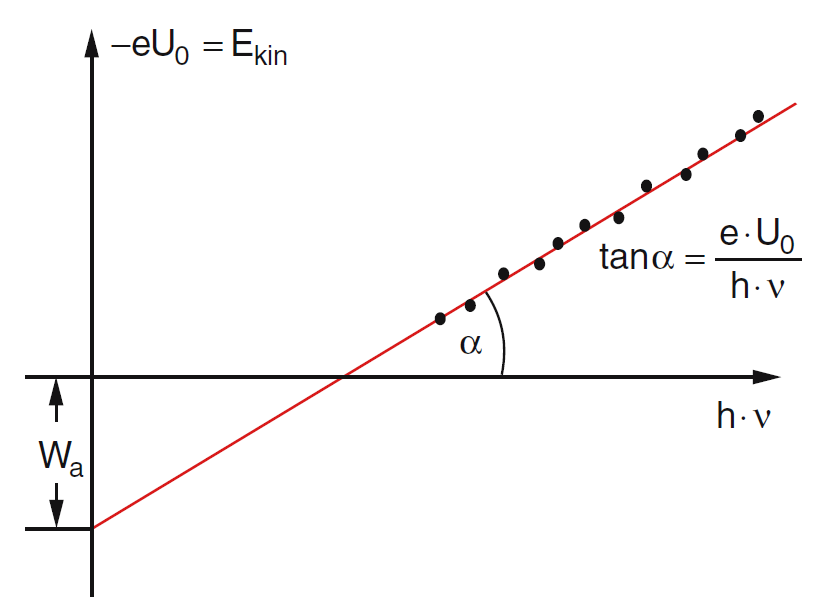
El efecto fotoeléctrico puede ser investigado con esta simulación. Se puede realizar un experimento virtual para determinar la constante de Planck y la “función de trabajo” W _a.

http://www.walter-fendt.de/ph14e/photoeffect.htm

Momento de fotones

Según Einstein los fotones deben poseer no solo energía sino impulso, también: Un cuántico de luz con frecuencia\( \nu \), cuya longitud de onda en vacío es\( \lambda=c / \nu \), tiene impulso

\( \mathbf{p}=\frac{h \nu}{c} \hat{\mathbf{k}}=\frac{h}{\lambda} \hat{\mathbf{k}}=\hbar \mathbf{k} \)(1.7)

donde k es un vector unitario que apunta en la dirección de la propagación del campo de luz que se supone que es una onda plana monocromática,\( \mathbf{k}=k \hat{\mathbf{k}} \) es el vector llamado onda-número con valor absoluto\( k=2 \pi / \lambda \). Este valor de p está de acuerdo con la relación fundamental de relatividad, válida para cualquier partícula de masa de reposo m ₀:

\( E^{2} / c^{2}-p^{2}=\left(m_{0} c\right)^{2} \)(1.8)

asumiendo que la masa de reposo del fotón es m ₀ =0.

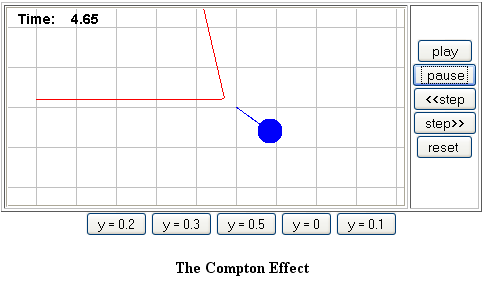
El efecto Compton

Entre las diversas evidencias de la hipótesis fotónica, una muy importante es el efecto Compton, que se ve en la figura 1.4. En este experimento, realizado por Arthur Compton, un rayo X de longitud de onda\(\lambda_{0}\) cae sobre una muestra y expulsa electrones de la misma. También aparece un rayo X secundario, cuya longitud de onda\(\lambda_{s}\) y dirección, dada por el ángulo φ, es diferente a la original. Estos se pueden medir mediante el experimento que se muestra en la figura 1.4.

Figura 1.4: Configuración experimental para el experimento de dispersión Compton.

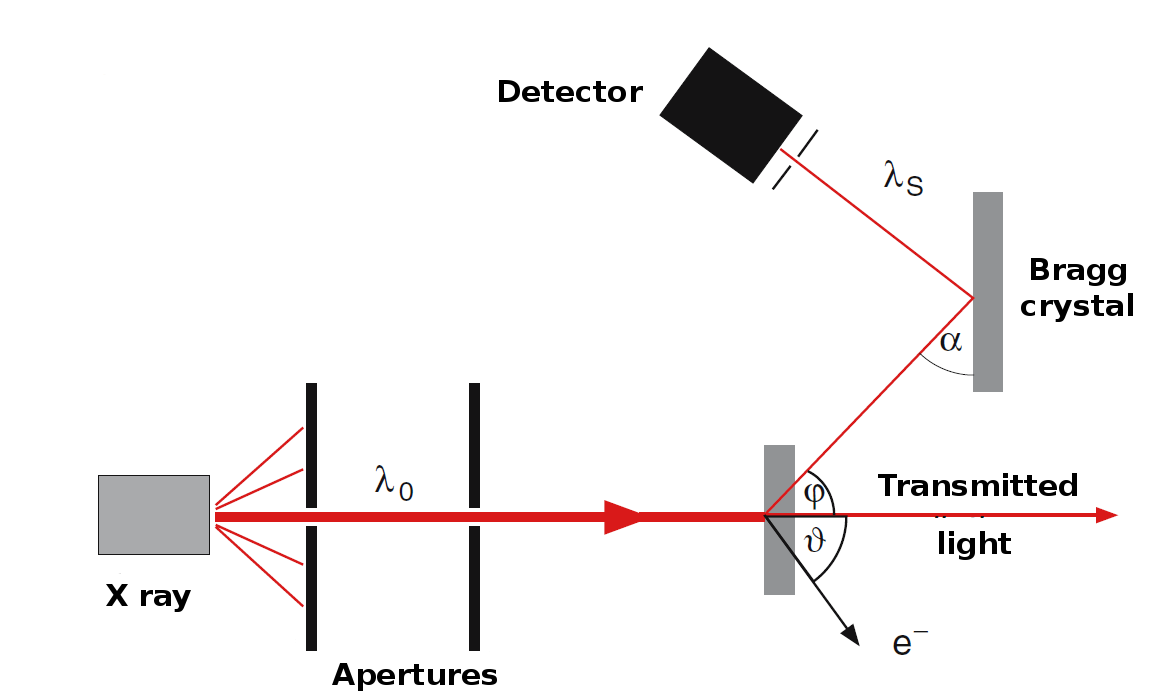
Podemos considerar el efecto como la dispersión del fotón sobre el electrón donde ambos son objetos puntiagudos clásicos. La conservación de la energía y el impulso requiere:

\ (\ begin {alineado}
h\ nu_ {0} +E_ {0} &=h\ nu_ {s} +E_ {e}\
\ frac {h\ nu_ {0}} {c} &=\ frac {h\ nu_ {s}} {c}\ cos\ varphi+p_ {e}\ cos\ vartheta\
0 &=\ frac {h\ nu_ {s}} {c}\ sin\ varphi-p_ {e}\ sin\ vartheta
\ fin {alineado}\) (1.9)

Aquí\(E_{0}=m_{e} c^{2}\) está la energía de descanso del electrón,\(E_{e}\) y\(p_{e}\) están la energía y el impulso del electrón después de la colisión

\(E_{e}=\frac{m_{e} c^{2}}{\sqrt{1-v^{2} / c^{2}}}, \quad p_{e}=\frac{m_{e} v}{\sqrt{1-v^{2} / c^{2}}}\)(1.10)

según las fórmulas relativistas.

Figura 1.5: El fotón de rayos X que se aproxima desde la izquierda se dispersa sobre el electrón.

Ambos son tratados como objetos puntiformes clásicos A partir de las tres ecuaciones anteriores, y usando\( \nu=c / \lambda \) obtenemos con algo de álgebra el resultado

\(\lambda_{s}-\lambda_{0}=\frac{h}{m_{e} c}(1-\cos \varphi)\)(1.11)

(Estrictamente hablando el resultado es válido para electrones libres en reposo. En los experimentos los electrones se liberan de los átomos, donde tienen alguna energía de unión negativa, pero esto se puede descuidar en comparación con otras energías que ocurren aquí). La expresión anterior conecta el cambio de la longitud de onda del fotón de rayos X durante la dispersión y el ángulo de dispersión φ. Los experimentos de Compton aprobaron el resultado teórico. La longitud

\(\lambda_{C}=\frac{h}{m_{e} c}=2.43 \times 10^{-12} \mathrm{~m}\)(1.12)

se llama la longitud de onda Compton del electrón. Tenga en cuenta que a veces el valor\(\tilde{\lambda}_{C}=\frac{\hbar}{m_{e} c}=\frac{\lambda_{C}}{2 \pi}\) se llama la longitud de onda Compton.

Animación

Estudia el efecto Compton con la animación en la página y responde las preguntas que allí aparecen.

http://physics.bu.edu/~duffy/semeste...5_compton.html

De acuerdo con estos experimentos el campo electromagnético puede manifestarse de ser de naturaleza discreta, y para una frecuencia y dirección de propagación dadas, interactúa como una partícula con la materia atómica con la energía e impulso correspondientes.

Ondas de probabilidad para partículas masivas

Después de que la hipótesis fotónica hubiera demostrado ser cierta, muchos físicos intentaron conciliar las dos visiones, cómo es posible que la luz se comporte como una especie de onda, mientras que consiste en cuantos o partículas que tienen energía e impulso. Si bien estos intentos no tuvieron éxito, surgió otra visión. L. de Broglie, un físico francés, estableció la hipótesis de que tal vez se pueda explicar el comportamiento de los electrones en los átomos, si se asume que los electrones —que se sabía que eran partículas masivas y que poseen carga negativa bien definida— también podrían comportarse como ondas. Posteriormente, esta suposición fue probada experimentalmente por G. P. Thomson, e independientemente por Davisson. La propiedad de que un electrón al igual que los fotones puede comportarse ya sea como una partícula o como una onda se llama dualidad. Esta propiedad tan inesperada fue resuelta por Max Born en 1926 por argumentos puramente teóricos. Pero antes de explicar la idea de Born, volvamos a un experimento que revela explícitamente la propiedad de la dualidad. Se trata del famoso experimento de doble rendija —uno de los experimentos más interesantes de la física— realizado por primera vez con electrones por Clauss Jönsson en 1961 y popularizado posteriormente por Akira Tonomura.

Animación

El experimento visto en la Fig. 1.6 fue realizado por primera vez por Clauss Jönsson en 1961. Una famosa variante del experimento la realizó Akira Tonomura, puso visiblemente disponible el resultado, cuyo video se muestra aquí.

http://titan.physx.u-szeged.hu/~mmqu...eslitTono.mpeg

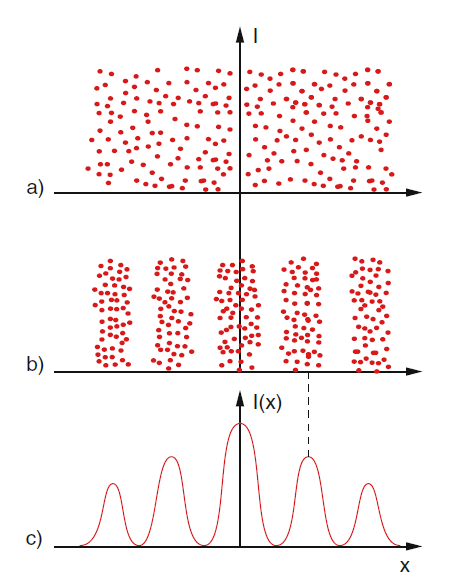
Al observar el experimento con más detalle, resulta que la imagen está formada por impactos puntuales individuales de partículas, como se ve en la secuencia de la figura 1.6. Un resultado definitivamente diferente al caso de las olas de agua.

Figura 1.6: Resultado del experimento de doble rendija con electrones. Secuencia de las figuras a, b, c, d, e muestra los electrones que llegan a la pantalla con el tiempo de exposición creciente. El patrón de interferencia está formado por impactos puntuales individuales de las partículas. Para entender el comportamiento ondular de las partículas cuánticas es necesario introducir una interpretación probabilística. http://commons.wikimedia.org/wiki/Fi...Tanamura_2.jp

Este fenómeno extraordinariamente sorprendente puede explicarse con el concepto fundamental de la mecánica cuántica: llamada amplitud de probabilidad. Consideraremos solo una de las coordenadas, la coordenada x que es perpendicular a las franjas que se ven en la pantalla donde se detectan las partículas. No sabemos exactamente cuál era el estado de la partícula antes de llegar a la pantalla. Este estado será denotado por\(\psi\). Pero sabemos que después de caer sobre la pantalla nos damos cuenta de que está en un lugar digamos x ₁. Este evento se caracterizará por un número complejo por el que se denotará\(\left\langle x_{1} \mid \psi\right\rangle\). Entonces a cada x le atribuimos un número complejo\(\left\langle x \mid \psi\right\rangle\). Considerando todos los valores x posibles obtenemos una función de x, que es una función valorada compleja de la variable real — la posición de la partícula — x:

\(\langle x \mid \psi\rangle=\psi(x)\)(1.13)

Esta función se utilizará para caracterizar el estado de la partícula, y esta función se denomina función de onda de coordenadas. La ley importante de la mecánica cuántica es que la probabilidad de encontrar la partícula alrededor de x en un pequeño intervalo dx es\(|\psi(x)|^{2} d x\). En el lenguaje de la teoría de probabilidad,\(|\psi(x)|^{2}\) se encuentra la función de densidad de probabilidad de la coordenada de la partícula que es una variable aleatoria. Así que tenemos

\(|\langle x \mid \psi\rangle|^{2}=|\psi(x)|^{2}=\psi^{*}(x) \psi(x)=: \rho(x) \geq 0\)(1.14)

En mecánica cuántica utilizamos la notación\(\rho(x)\) para la distribución de probabilidad. La probabilidad de encontrarlo en un punto x en el intervalo\(x_{1}<x<x_{2}\) viene dada por:

\(P\left(x_{1}<x<x_{2}\right)=\int_{x_{1}}^{x_{2}}|\psi(x)|^{2} d x=\int_{x_{1}}^{x_{2}} \rho(x) d x\)(1.15)

que es válido para arbitrarios\(x_{1}<x_{2}\). La probabilidad de encontrar la partícula en algún lugar del eje real debe ser 1, por lo tanto:

\(\int_{-\infty}^{\infty} \rho(x) d x=\int_{-\infty}^{\infty}|\psi(x)|^{2} d x=1\)(1.16)

En consecuencia, la función de onda que describe una partícula debe ser tal que la integral de su valor absoluto cuadrado entre −∞ y ∞ debe dar 1.

El patrón de interferencia visto en la Fig 1.6 puede explicarse por las reglas de la mecánica cuántica, como lo haremos a continuación. La partícula que se suponía que estaba en un estado ψ ψ puede llegar a la primera hendidura en la pantalla, y este estado, es decir, partícula en la primera hendidura se denotará por\(\psi_{1}\). La amplitud correspondiente es entonces\(\left\langle\varphi_{1} \mid \psi\right\rangle\). Continuando su camino llega en algún lugar a la segunda pantalla, donde se registra en el punto x. La amplitud correspondiente a esta segunda parte de su camino es\(\left\langle x \mid \varphi_{1}\right\rangle\). La amplitud total que pertenece al proceso que la partícula llega a xx a través de la hendidura 1 es el producto de las dos amplitudes\(\left\langle x \mid \varphi_{1}\right\rangle\left\langle\varphi_{1} \mid \psi\right\rangle\). De igual manera, la amplitud de la otra trayectoria posible de la partícula, que pasó por la hendidura 2 antes de llegar a x\(\psi_{2}\) es\(\left\langle x \mid \varphi_{2}\right\rangle\left\langle\varphi_{2} \mid \psi\right\rangle\), donde está el estado de la partícula, cuando está en la segunda hendidura. La amplitud total es la suma de las amplitudes de los dos caminos posibles.

\ (\ begin {alineado}
\ langle x\ mid\ psi\ rangle &=\ izquierda\ langle x\ mid\ varphi_ {1}\ derecha\ rangle\ izquierda\ langle\ varphi_ {1}\ mid\ psi\ right\ rangle+\ left\ langle x\ mid\ varphi_ {2}\ right\ rangle\ left\ langle\ varphi_ {2}\ mid\ psi\ right\ rangle,\ text {o equivalentemente}\\
\ psi (x) &=\ varphi_ {1} (x)\ izquierda\ langle\ varphi_ {1}\ mediados\ psi\ derecha\ rangle+\ varphi_ {2} (x)\ izquierda\ langle\ varphi_ {2}\ mediados\ psi\ derecha\ rangle=c_ {1}\ varphi_ {1} (x) +c_ {2}\ varphi_ {2} (x)
\ end {alineado}\) (1.17)

donde\(c_{1}=\left\langle\varphi_{1} \mid \psi\right\rangle\),\(c_{2}=\left\langle\varphi_{2} \mid \psi\right\rangle\). Estas últimas amplitudes se han establecido para ser dos números (complejos) en lugar de funciones, porque aquí hemos asumido que las rendijas son pequeñas, y no necesitamos distinguir entre las diferentes posiciones dentro de las rendijas. Lo pequeño que significa, se volverá más definido un poco más tarde. La suma de las amplitudes anteriores es la superposición de las dos posibilidades. La probabilidad de encontrar la partícula en la posición xx es el valor absoluto cuadrado de la suma de las dos amplitudes posibles:

\ (\ begin {alineado}
|\ psi (x) |^ {2} &=\ izquierda|c_ {1}\ varphi_ {1} (x)\ derecha|^ {2} +\ izquierda|c_ {2}\ varphi_ {2} (x)\ derecha|^ {2} +c_ {1} ^ {*} c_ {2}\ varphi_ {1}} ^ {*} (x)\ varphi_ {2} (x) +c_ {1} c_ {2} ^ {*}\ varphi_ {1} (x)\ varphi_ {2} ^ {*} (x)\
&=\ izquierda|c_ {1}\ derecha|^ {2}\ izquierda|\ varphi_ {1} (x)\ derecha|^ {2}\ izquierda|\ varphi_ {1} (x)\ ^ {2} +\ izquierda|c _ {2}\ derecha|^ {2}\ izquierda|\ varphi_ {2} (x)\ derecha|^ {2} +2\ nombreoperador {Re}\ izquierda (c_ {1} ^ {*} c_ {2}\ varphi_ {1} ^ {*} (x)\ varphi_ {2} (x)\ derecha)
\ end {alineado}\) (1.18)

La interferencia aparece por el último término. Habrá lugares donde las partículas lleguen con una probabilidad pequeña, estas serán las franjas oscuras, mientras que habrá lugares donde las probabilidades de detección sean grandes. La mecánica cuántica da la forma explícita de las dos funciones\(\varphi_{1}(x)\) y\(\varphi_{2}(x)\), pero no vamos a ocuparnos de esto aquí.

No podemos decir cuál de las rendijas atravesó la partícula, el patrón de interferencia es el testigo de que pasó simultáneamente por ambas. Se puede demostrar, que si tratamos de detectar de alguna manera qué camino ha tomado la partícula, entonces una detección exitosa destruirá el patrón de interferencia, por lo que no podemos ver simultáneamente el patrón de interferencia y distinguir entre las dos formas en que avanzó la partícula. El mismo experimento se ha realizado con partículas mayores que los electrones, como neutrones, átomos, moléculas pequeñas. Más recientemente el efecto se demostró con el objeto molecular llamado fullereno, que consta de 60 átomos de carbono.

No enfatizamos hasta ahora, pero es importante que la amplitud, es decir, la función de onda dependa también del tiempo. Si deseamos hacer uso de funciones de onda dependientes del tiempo lo denotaremos con una letra griega mayúscula:\(\Psi(x, t)\). ¿Cómo se ve esa función en cualquier caso concreto? Esto depende de la situación física en cuestión, y uno de los problemas importantes de la mecánica cuántica es encontrar la forma de esta función. En general tenemos que prescribir la propiedad de integrabilidad cuadrada con respecto a x, ya que para cualquier valor fijo de la variable de tiempo t\(|\Psi(x, t)|^{2}\) es la densidad de probabilidad de la coordenada de la partícula. Esta interpretación de la función de onda fue dada por primera vez por Max Born. En consecuencia:

\(\int_{-\infty}^{\infty}|\Psi(x, t)|^{2} d x=1\)(1.19)

en cualquier momento instante. Decimos entonces que\(\Psi(x, t)\) se normaliza a la unidad. Este requisito será (i) refinado posteriormente y (ii) requerirá ciertas prescripciones sobre cómo la función de onda debe depender de la variable de tiempo.

Si queremos dar la posición de la partícula en el espacio tridimensional, en lugar de la línea, entonces la función de onda dependerá de las tres coordenadas de los puntos en el espacio:\(\Psi(x, y, z, t)=\Psi(\mathbf{r}, t)\). Aquí la variable aleatoria será el vector de posición de la partícula. La densidad de probabilidad es entonces la función\(|\Psi(\mathbf{r}, t)|^{2}\), para lo cual se prescribe la normalización en tres dimensiones.

Figura 1.7:

Volviendo a una dimensión, una función de onda de uso frecuente (real en este caso específico) para una partícula localizada más o menos alrededor del origen se encuentra\(\psi(x)=\mathcal{N} e^{-x^{2} / 4 \sigma_{0}^{2}}\) en un instante dado, donde σ ₀ es una constante independiente de x, mientras que\(\mathcal{N}\) es un factor de normalización. La densidad de probabilidad correspondiente es\(|\psi(x)|^{2}=: \rho(x)=\mathcal{N}^{2} e^{-x^{2} / 2 \sigma_{0}^{2}}\). Su integral a lo largo del eje real debe dar 1, esta es la condición que determina el factor\(\mathcal{N}\). Como se sabe por la teoría de probabilidad, esta es la densidad de probabilidad de la llamada normal estándar, o función de distribución gaussiana, si\(\mathcal{N}=\left(2 \pi \sigma^{2}\right)^{-1 / 4}\).

Problema 1.1

Demostrar que el factor de normalización en\(|\psi(x)|^{2}=: \rho(x)=\mathcal{N}^{2} e^{-x^{2} / 2 \sigma_{0}^{2}} \text { is } \mathcal{N}=\left(2 \pi \sigma^{2}\right)^{-1 / 4}\).

Según lo que dijimos antes, la función también puede depender del tiempo, de modo que en lugar de σ ₀ podamos tener una σ (t) dependiente del tiempo en ella, y entonces por supuesto (\ mathcal {N}\) también será dependiente del tiempo. Además de la función de onda gaussiana anterior hay muchas otras posibilidades dependiendo del problema físico en cuestión.

Posteriormente, consideraremos en detalle el problema de la dinámica del estado, lo que significa que consideraremos cómo el estado, es decir, la función de onda cambia con el tiempo dada una fuerza o un potencial que actúa sobre la partícula.

Problema 1.2

Investigando el fotoefecto con una fotocélula donde el cátodo está cubierto por Cesio los electrones se detienen si el voltaje es mayor a 0.33V para una onda de luz de longitud de onda 546nm, mientras que el valor correspondiente para 365nm es 1.46V. Derivar el valor de la constante de Planck a partir de estos resultados. ¿Cuál es la función de trabajo del Cesio? ¿Cuánto es el voltaje de parada usando luz de 436nm? ¿Cuál es la longitud de onda umbral que produce emisión de electrones?

Problema 1.3

Estimar el costo de un fotón verde en el caso de una bombilla tradicional de 100W que funcione con 5% de eficiencia, y encendida por 1 segundo.

Problema 1.4

Derivar el resultado

\(\lambda_{s}-\lambda_{0}=\frac{h}{m_{e} c}(1-\cos \varphi)\)(1.20)

para la dispersión de Compton usando las ecuaciones que expresan la conservación de la energía y el impulso:

\ (\ begin {alineado}
h\ nu_ {0} +E_ {0} &=h\ nu_ {s} +E_ {e}\
\ frac {h\ nu_ {0}} {c} &=\ frac {h\ nu_ {s}} {c}\ cos\ varphi+p_ {e}\ cos\ vartheta\
0 &=\ frac {h\ nu_ {s}} {c}\ sin\ varphi-p_ {e}\ sin\ vartheta
\ fin {alineado}\) (1.21)