2: Conceptos básicos de mecánica cuántica

Objetivos

En este capítulo presentamos la ecuación de Schrödinger, la ecuación dinámica que describe un sistema cuántico mecánico. Se discute el papel de los valores propios de la energía y las funciones propias en el proceso de búsqueda de sus soluciones. A través del problema del oscilador armónico lineal se demuestra la forma en que se resuelven los problemas mecánicos cuánticos. Finalmente se discute el valor de expectativa y la varianza de un operador.

Prerrequisitos

Elementos de ecuaciones diferenciales, y el material del Capítulo 1. Las ecuaciones clásicas de los movimientos. El oscilador armónico clásico.

La ecuación de Schrödinger

Como hemos visto en la sección anterior, el estado de una partícula en el espacio de posición se describe mediante una función de onda\(\Psi(x, t)\) en una, o\(\Psi(\mathbf{r}, t)\) en tres dimensiones. Esta es una amplitud de probabilidad, y\(\left.\Psi(\mathbf{r}, t)\right|^{2}\) es la densidad de probabilidad de encontrar la partícula en algún lugar del espacio alrededor de la posición dada por el vector r. Fue Erwin Schrödinger quien escribió la ecuación, cuyas soluciones nos dan la forma concreta de la función. Su ecuación fundamental se llama ecuación de Schrödinger dependiente del tiempo, o ecuación dinámica, y tiene la forma:

\(i \hbar \frac{\partial \Psi(\mathbf{r}, t)}{\partial t}=-\frac{\hbar^{2}}{2 m} \Delta \Psi(\mathbf{r}, t)+V(\mathbf{r}) \Psi(\mathbf{r}, t)\)(2.1)

Para simplificar el tratamiento consideramos en esta subsección el movimiento unidimensional a lo largo del eje x:

\(i \hbar \frac{\partial \Psi(x, t)}{\partial t}=-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi(x, t)}{\partial x^{2}}+V(x) \Psi(x, t)\)(2.2)

Figura 2.1:

En mecánica cuántica el lado derecho de la ecuación de Schrödinger se escribe en breve como\(\hat{H} \Psi(x, t)\), por lo que (2.2) puede escribirse como

\(i \hbar \frac{\partial \Psi(x, t)}{\partial t}=\hat{H} \Psi(x, t)\)(2.3)

Esta notación tiene una razón más profunda, la cual se explica aquí en breve. La operación\(-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi(x, t)}{\partial x^{2}}+V(x) \Psi(x, t)\) puede considerarse como una transformación de la función\(\Psi(x, t)\), y el resultado es otra función de x y t. Esto significa que el lado derecho es un mapeo (específico) del conjunto de funciones para dar de nuevo una función. El mapeo es lineal, y

\(\hat{H}=-\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}+V(x)\)(2.4)

es una transformación lineal u operador lineal, como se le llama en la mecánica cuántica. Al operador en cuestión\(\hat{H}\) se le llama el operador de la energía, que lleva el nombre el operador Hamilton o el hamiltoniano para abreviar. Posteriormente, además\(\hat{H}\) nos encontraremos con otro tipo de operadores lineales, correspondientes a cantidades físicas distintas a la energía. La forma (2.4) del Hamiltoniano se utiliza para el problema específico de una partícula que se mueve en una dimensión x, donde el campo de fuerza externo dado por la función de energía potencial\(V(x)\). Para otros problemas la expresión del hamiltoniano es diferente, pero la ecuación dinámica en la forma (2.3) es la misma. Esto es como en la mecánica clásica donde la ecuación de movimiento para una partícula es siempre\(\dot{\mathbf{p}}=\mathbf{F}\) pero\(\mathbf{F}\), la fuerza depende de la situación física en cuestión. En la mecánica cuántica, la ecuación de Schrödinger reemplaza la ecuación de movimiento de Newton de la mecánica clásica que muestra su significado fundamental.

Aquí enumeramos algunas propiedades importantes de la ecuación (2.2), o equivalentemente las de la ecuación (2.3):

• Se trata de una ecuación lineal, lo que significa que si\(\Psi_{1}(x, t)\) y\(\Psi_{2}(x, t)\) son soluciones de la ecuación, entonces las combinaciones lineales de la forma también\(c_{1} \Psi_{1}+c_{2} \Psi_{2}\) serán una solución, donde\(c_{1}\) y\(c_{2}\) son constantes complejas. La suma puede extenderse a sumas infinitas, (con ciertas restricciones matemáticas). La linealidad es válida, porque en ambos lados de la ecuación tenemos operaciones lineales, derivaciones y multiplicación con la función dada\(V(x)\).
• Otra propiedad importante es que la ecuación es de primer orden en el tiempo. Por lo tanto, si damos una función inicial en\(t = t_{0}\) dependiendo solo de x:\(\Psi\left(x, t_{0}\right) \equiv \psi_{0}(x)\), entonces resolviendo la ecuación podemos encontrar —en principio— una solución única que satisfaga esta condición inicial. Por supuesto, hay infinitamente muchas soluciones posibles, pero corresponden a diferentes condiciones iniciales. La dependencia del tiempo de la función de onda de una condición inicial dada se llama evolución del tiempo.
• La ecuación conserva la norma de la función de onda, lo que significa que si\(\Psi(x, t)\) obedece (2.2), entonces la integral de la densidad de probabilidad de posición con respecto a x es constante independientemente de t. Específicamente, si esta integral es igual a 1 en t ₀, entonces permanece así para todo momento.

\(\int_{-\infty}^{\infty}\left|\psi_{0}(x)\right|^{2} d x=1 \Longrightarrow \int_{-\infty}^{\infty}|\Psi(x, t)|^{2} d x=1, \quad \forall t\)(2.5)

En otras palabras, la propiedad de normalización sigue siendo válida para todos los tiempos. Esta propiedad se llama unitariedad de la evolución del tiempo. La prueba de esta afirmación se deja como un problema.

Problema 2.1

Usando (2.2) demostrar que la derivada de tiempo de la condición de normalización es cero, lo que significa la validez de (2.5).

Estados estacionarios

Se pueden encontrar soluciones específicas de la ecuación (2.2) haciendo que el “ansatz” (esta palabra alemana utilizada también en textos matemáticos en inglés, y significa conjetura educada), que la solución es producto de dos funciones

\(\Psi(x, t)=a u(t) u(x)\)(2.6)

donde\(au(t)\) depende sólo del tiempo, mientras que\(u(x)\) es una función dependiente del espacio. Este procedimiento se llama separación. No todas las soluciones de la Ec. (2.2) tienen esta forma separada, pero es útil encontrar primero este tipo de soluciones. Sustituyendo de nuevo el producto (2.6) en (2.2), encontramos

\(i \hbar u(x) \frac{\partial a u(t)}{\partial t}=\left(-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} u(x)}{\partial x^{2}}+V(x) u(x)\right) a u(t)\)(2.7)

Dividiendo por\(au(t)u(x)\), obtenemos:

\(i \hbar \frac{1}{a u(t)} \frac{\partial a u(t)}{\partial t}=\frac{1}{u(x)}\left(-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} u(x)}{\partial x^{2}}+V(x) u(x)\right)\)(2.8)

Como la función del lado izquierdo depende únicamente del tiempo, mientras que la del lado derecho depende únicamente de xx, y deben ser iguales para todos los valores de estas variables, esto es posible sólo si ambos lados son iguales a una constante independiente de x y t. Es fácil comprobar que la constante tiene que ser de dimensión de energía, y será denotada por ε. Obtenemos entonces dos ecuaciones. Uno de ellos es

\(i \hbar \frac{\partial a u(t)}{\partial t}=a u(t) \varepsilon\)(2.9)

con la solución

\(a u(t)=C e^{-i \varepsilon t / \hbar}\)(2.10)

donde C es una constante de integración.

La otra ecuación toma la forma:

\(-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} u(x)}{\partial x^{2}}+V(x) u(x)=\varepsilon u(x)\)(2.11)

Reconocemos que en el lado izquierdo tenemos ahora de nuevo al operador\(\hat{H}\) actuando esta vez en\(u(x)\):

\(\hat{H} u(x)=\varepsilon u(x)\)(2.12)

Este es un problema llamado de valor propio: el efecto del operador es tal que devuelve la función misma multiplicada por una constante. Como el operador aquí es el hamiltoniano, es decir, el operador de energía, (2.12) es una ecuación de valor propio de energía. A veces también se le llama la ecuación de Schrödinger (independiente del tiempo), pero no usaremos esta terminología.

Animación

Esta sencilla animación gif intenta visualizar los conceptos de vectores propios.

http://upload.wikimedia.org/Wikipedia/commons/0/06/Eigenvectors.gif

Animación

Arrastre cada vector hasta que el paralelogramo coloreado desaparezca. Si puedes hacer esto para dos vectores independientes, forman una base de vectores propios y la matriz del mapa lineal se vuelve diagonal, es decir, los términos no diagonales son cero. Esto es imposible para algunas de las primeras matrices—pruébalas todas. Cuando hayas encontrado un vector propio, comprueba que puede prolongarse en su propia dirección sin dejar de ser un vector propio; es interesante vigilar la matriz al mismo tiempo.

http://demonstrations.wolfram.com/EigenvectorsByHand/

Es importante recalcar aquí que la Ec. (2.11) debe considerarse junto con ciertas condiciones límite para ser satisfechas por las soluciones\(u(x)\) en los límites de su dominio. En otras palabras, las condiciones límite son parte de la noción del operador diferencial\(\hat{H}\) en (2.11). Las condiciones límite se pueden elegir de varias maneras diferentes, y en general, se utilizan consideraciones físicas para elegir las adecuadas. En otras palabras, entre las soluciones de (2.11) hay que seleccionar aquellas especiales donde\(u(x)\) obedezca las condiciones límite que generalmente es posible solo para ciertos valores específicos de ε. Las funciones\(u_{ε}(x)\) que obedecen a la ecuación con las condiciones de límite dadas se denominan funciones propias de\(\hat{H}\) pertenecer al valor propio de energía correspondiente ε:\(\hat{H} u_{\varepsilon}(x)=\varepsilon u_{\varepsilon}(x)\).

Según la condición de separación todas las funciones de la forma

\(\psi_{\varepsilon}(x, t)=u_{\varepsilon}(x) e^{-i \varepsilon t / \hbar}\)(2.13)

serán las soluciones de la ecuación de Schrödinger (2.2). Los valores propios de energía permitidos εε, seleccionados por las condiciones de contorno pueden ser discretos, luego suelen ser etiquetados por enteros\(ε_{n}(n=1, 2,⋯)\), pero también pueden ser continuos. En este último caso se encuentran soluciones adecuadas para todos los ε -s dentro de un cierto intervalo de energía. Se puede demostrar fácilmente que las soluciones físicamente aceptables deben pertenecer a valores propios de energía real.

Problema 2.2

Mostrar que la condición de normalización solo permite valores reales de ε.

En general, hay infinitamente muchas soluciones de la forma (2.13), pero no agotan todas las soluciones. Como la ecuación hamiltoniana, así como la ecuación de Schrödinger son lineales, las combinaciones lineales apropiadas de las soluciones específicas (2.13) también obedecen a la ecuación de Schrödinger, y tienen la forma general:

\(\Psi(x, t)=\sum_{n} c_{n} u_{n}(x) e^{-i \varepsilon_{n} t / \hbar}+\int c(\varepsilon) u_{\varepsilon}(x) e^{-i \varepsilon t / \hbar} d \varepsilon\)(2.14)

Aquí los números complejos cncn y la función compleja\(c(ε)\) son arbitrarios, la única condición es que los resultantes\(Ψ(x,t)\) deben ser normalizables, es decir, deben ser tales que la condición\(\int|\Psi(x, t)|^{2} d x=1\) debe mantenerse.

También se puede demostrar —aunque esto suele estar lejos de ser simple— que para las funciones energéticas potenciales físicamente adecuadas, u\(\hat{H}\) operadores, todas las soluciones de (2.2) pueden escribirse en la forma dada por (2.14).

Se considera que las soluciones\(ψ_{ε}(x,t)\) de la forma (2.13) son específicas en el sentido de que contienen solo un término a partir de la suma o integral en (2.14). Por lo tanto, las distribuciones de probabilidad correspondientes a estas soluciones:\(\left|\psi_{\varepsilon}(x, t)\right|^{2}=\left|u_{\varepsilon}(x)\right|^{2}\) no dependen del tiempo, mientras que las funciones de onda es decir, las amplitudes de probabilidad son dependientes del tiempo. Estas funciones de onda, y los estados físicos correspondientes se denominan estados estacionarios. Según (2.14) se puede obtener una solución general por una expansión en términos de los estados estacionarios.

El conjunto de todos los valores propios se llama el espectro del\(\hat{H}\) operador, o el espectro de energía. Obsérvese que esta terminología es diferente de la noción del espectro en la espectroscopia experimental, pero —como veremos— están relacionados entre sí. En la espectroscopia experimental se denomina término a un valor propio de energía, y el espectro visto, por ejemplo, en la espectroscopia óptica es la frecuencia correspondiente a las diferencias de valores propios de energía. Las funciones propias de energía que pertenecen a valores propios dados se pueden identificar con los estados estacionarios (órbitas) postulados por Bohr. Por lo tanto, la existencia de estados estacionarios es la prueba mecánica cuántica del primer postulado de Bohr. Además QM también nos da el método de cómo encontrar las energías y funciones de onda de los estados estacionarios.

Ahora introduciremos la siguiente propiedad importante de las funciones propias de\(\hat{H}\). Se puede probar, que la integral del producto\(u_{n}^{*}(x) u_{n^{\prime}}(x)\) de las funciones propias pertenecientes a diferentes valores propios se\(\varepsilon_{n} e q \varepsilon_{n^{\prime}}\) desvanece\(\int u_{n}^{*}(x) u_{n^{\prime}}(x) d x=0\), donde los límites de la integración se toman sobre el dominio de las funciones propias, generalmente entre\(−∞\) y\(∞\). Esta propiedad se llama ortogonalidad de las funciones propias. Si además prescribimos la normalización de las funciones propias, que siempre se puede lograr multiplicando por una constante apropiada, podemos escribir

\(\int u_{n}^{*}(x) u_{n^{\prime}}(x) d x=\delta_{n n^{\prime}}\)(2.15)

donde\(\delta_{n n^{\prime}}\) está el símbolo de Kronecker. Aquí se toma conjuntamente tanto la ortogonalidad como la normalización, y decimos por lo tanto que las funciones propias son ortonormales.

Aquí hay un punto un poco más complicado pero importante. Puede resultar, que uno encuentre varias soluciones linealmente independientes de (2.11) con una y la misma ε. Que sea el número de estas soluciones pertenecientes a ε\(g_{ε}\). Decimos que ε es\(g_{ε}\) tiempos degenerados. También se puede probar que entre las soluciones degeneradas hay ortogonales cuyo número es\(g_{ε}\). Podemos escribir esto de la siguiente manera:

\(\int u_{n k}^{*}(x) u_{n k^{\prime}}(x) d x=\delta_{k k^{\prime}}\)(2.16)

donde\(u_{nk}(x)\) significa la k-ésima solución que pertenece a un dado\(\varepsilon_{n}: k=1,2 \ldots g_{\varepsilon_{n}}\).

Problema 2.3

Mostrar que la densidad de probabilidad obtenida de la combinación lineal de dos estados estacionarios pertenecientes a diferentes valores propios de energía depende del tiempo. ¿Cuál es la dependencia característica del tiempo de esta densidad de probabilidad?

Un ejemplo: el oscilador armónico lineal

Este es un sistema muy importante tanto en la física clásica como en la cuántica, por lo que además de demostrar la forma en que se resuelven problemas mecánicos cuánticos, tiene aplicaciones de gran alcance en todas las ramas de la física teórica

La energía potencial es\(\frac{1}{2} D x^{2}=\frac{1}{2} m \omega^{2} x^{2}\), y la ecuación del valor propio es

\(-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} u}{\partial x^{2}}+\frac{1}{2} m \omega^{2} x^{2} u(x)=\varepsilon u(x)\)(2.17)

donde\(−∞<x<∞\)

Será útil introducir la coordenada adimensional y la energía adimensional, mediante las relaciones:

\(\xi=\sqrt{m \omega / \hbar} x, \quad \epsilon=\frac{2 \varepsilon}{\hbar \omega}\)(2.18)

Obtenemos de (2.17)

\(\frac{\partial^{2} u}{\partial \xi^{2}}+\left(\epsilon-\xi^{2}\right) u=0\)(2.19)

Primero encontramos la solución asintótica de esta ecuación. Para grandes valores de\(|\xi|\) tenemos\(\frac{\partial^{2} u}{\partial \xi^{2}}-\xi^{2} u=0\), con la solución aproximada\(e^{-\xi^{2} / 2}\). (El término\(\xi^{2} e^{-\xi^{2} / 2}\) dominará\(e^{-\xi^{2} / 2}\) para grandes\(|\xi|\)) La otra posibilidad\(e^{+\xi^{2} / 2}\) debe omitirse, porque no es integrable cuadrada, por lo que no es una función permitida para describir un estado cuántico.

Las soluciones exactas de (2.19) se encuentran en la forma

\(u(\xi)=\mathcal{H}(\xi) e^{-\xi^{2} / 2}\)(2.20)

donde\(\mathcal{H}(\xi)\) es un polinomio de\(\xi\). Sustituyendo esta suposición en 2.19, obtenemos la ecuación

\(\frac{d^{2} \mathcal{H}}{d \xi^{2}}-2 \xi \frac{d \mathcal{H}}{d \xi}+(\epsilon-1) \mathcal{H}=0\)(2.21)

Esto se conoce como la ecuación diferencial para los polinomios de Hermite. Buscando su solución como una serie de potencias\(\mathcal{H}=\sum_{k} a_{k} \xi^{k}\), encontramos que los coeficientes tienen que obedecer la condición de recursión

\((2 k-\epsilon+1) a_{k}=(k+2)(k+1) a_{k+2}\)(2.22)

Problema 2.4

Derivar (2.21) de la suposición (2.20) y (2.19). Derivar la fórmula de recursión, para los coeficientes de la serie de potencias.

En caso de que la serie sea infinita, para k -s grandes tendríamos\(a_{k+2} \simeq 2 k a_{k}\), que se obtiene manteniendo solo los términos de orden más alto en k en ambos lados. Esta relación de recursión es, sin embargo, la propiedad de la serie de la\(e^{\xi^{2}}\) cual conduciría a una función integrable no cuadrada como sería entonces de nuevo la forma asintótica de u\(e^{\xi^{2}} e^{-\xi^{2} / 2}=e^{\xi^{2} / 2}\). Por lo tanto, la suma determinante\(\mathcal{H}\) debe permanecer finita, y así tiene que terminar en una determinada potencia entera, la denotaremos por\(\nu\). Esto significa que todos los coeficientes mayores que\(\nu\) son cero, y en particular:

\(a_{\nu} e q 0, \quad a_{\nu+1}=0, \quad a_{\nu+2}=0\)(2.23)

En otras palabras\(\mathcal{H}\) es un polinomio de grado\(\nu\), y la condición\(a_{\nu+1}=0\) requiere entonces que todos los coeficientes\(0=a_{\nu-1}=a_{\nu-3}=\ldots\) por lo que los polinomios sean pares o impares, dependiendo de\(\nu\). En vista de 2.23 obtenemos 2.22 eso\(2\nu-\epsilon+1=0\), o\(\epsilon=2\nu+1\).

Para resumir el resultado, la ecuación de valor propio tiene soluciones integrables cuadradas solo si

\(\varepsilon_{\nu}=\hbar \omega\left(\nu+\frac{1}{2}\right), \quad \nu=0,1,2 \ldots\)(2.24)

donde\(\nu\) se llama el número cuántico vibracional. Los posibles valores de energía del oscilador armónico son equidistantes con la separación\(Δε=ℏω\). La energía más baja para\(\nu=0\), no\(\varepsilon_{0}=\hbar \omega / 2\) es cero, sino que equivale a la mitad de la separación de niveles. ε ₀ se llama energía de punto cero.

Las funciones propias correspondientes son

\(u_{\nu}(x)=\mathcal{N}_{\nu} \mathcal{H}_{\nu}\left(\sqrt{\frac{m \omega}{\hbar}} x\right) e^{-\frac{m \omega}{\hbar} x^{2} / 2}\)(2.25)

donde\(\mathcal{H}_{\nu}\) -s son polinomios de grado\(\nu\), llamados polinomios hermitas, y\(\mathcal{N}_{\nu}\) -s son coeficientes de normalización. La integrabilidad cuadrada está asegurada por el factor exponencial. Para el coeficiente de no fuga más alto de\(\mathcal{H}_{\nu}\), que no está determinado por la recursión, la convención es establecer\(a_{\nu}=2^{\nu}\).

Figura 2.2: Funciones propias de energía del oscilador armónico lineal.

Problema 2.5

Determinar los 3 primeros polinomios hermitas

Se puede demostrar que los\(\epsilon_{\nu}\) valores propios son no degenerados, por lo que la función propia\(u_{\nu}(x)\) es única (hasta un factor constante). Las funciones propias tienen también la importante propiedad de ser ortonormales:

\(\int_{-\infty}^{\infty} u_{\nu^{\prime}}(x) u_{\nu}(x) d x=\delta_{\nu^{\prime} \nu}\)(2.26)

Las soluciones generales dependientes del tiempo del problema del oscilador armónico son de la forma:

\(\Psi(x, t)=\sum_{\nu=0}^{\infty} c_{\nu} e^{-i \varepsilon_{\nu} t \hbar} u_{\nu}(x)=e^{-i \omega t / 2} \sum_{\nu=0}^{\infty} c_{\nu} e^{-i \nu \omega t} u_{\nu}(x)\)(2.27)

donde los coeficientes cvcv son constantes complejas, obedeciendo a la condición de normalización\(\sum_{\nu=0}^{\infty}\left|c_{\nu}\right|^{2}=1\). Están determinados por la condición inicial

\(\Psi(x, 0)=\sum_{\nu=0}^{\infty} c_{\nu} u_{\nu}(x), \quad \text { as lquad } c_{\nu}=\int_{-\infty}^{\infty} u_{\nu}(x) \Psi(x, 0) d x\)(2.28)

de acuerdo con la condición de ortonormalidad.

Animación

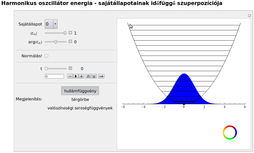
Esta animación muestra la evolución temporal del oscilador armónico simple si inicialmente se encuentra en la superposición del estado fundamental\((n=0)\) y el\(n=1\) estado.

\(\Psi(x, 0)=\frac{1}{\sqrt{2}}\left(\varphi_{0}(x)+\varphi_{1}(x)\right)\)

http://titan.physx.u-szeged.hu/~mmquantum/videok/Harmonikus_oszcillator_szuperpozicio_0_1.flv

Animación

Esta animación interactiva nos da una herramienta para jugar con las funciones propias del oscilador armónico lineal. Podemos construir diferentes combinaciones lineales de las funciones propias de la energía y estudiar su evolución en el tiempo.

http://titan.physx.u-szeged.hu/~mmquantum/download.php?download_file=HarmonikusOszcillatorIdofuggoSzuperpozicio.nbp

Valores de expectativa y operadores

La función de onda da la distribución de probabilidad de la posición de una partícula con la propiedad (2.5). Según la teoría de probabilidad, el valor de expectativa o valor medio de la posición de la partícula que se mueve en una dimensión viene dado por

\(\langle\hat{X}\rangle_{\psi}=\int_{-\infty}^{\infty} x|\psi(x)|^{2} d x=\int \psi^{*}(x) x \psi(x) d x\)(2.29)

el motivo de escribir capital\(\hat{X}\) se verá a continuación. No pusimos los límites deliberadamente en la segunda integral definitiva. En lo que sigue, si los límites no se muestran explícitamente, entonces la integración siempre va de\(−∞\) a\(+∞\), en una dimensión, y sobre todo el espacio tridimensional en tres dimensiones. Por lo tanto, de manera análoga para un movimiento tridimensional podemos definir el valor de expectativa del vector de radio como

\(\langle\hat{\mathbf{R}}\rangle_{\psi}=\int \mathbf{r}|\psi(\mathbf{r})|^{2} d^{3} \mathbf{r}=\int \psi^{*}(\mathbf{r}) \mathbf{r} \psi(\mathbf{r}) d^{3} \mathbf{r}\)(2.30)

lo que en realidad significa tres integrales diferentes para cada componente de\(\mathbf{r}\). Ahora supongamos que la partícula se mueve en un campo de fuerza externo dado por la energía potencial\(V(\mathbf{r})\). Si conocemos solo la distribución de probabilidad y no el valor exacto de la posición de las partículas no podemos hablar tampoco del valor de la energía potencial sino sólo de su distribución de probabilidad. El valor de expectativa de la energía potencial es

\(\langle V(\hat{\mathbf{R}})\rangle_{\psi}=\int \psi^{*}(\mathbf{r}) V(\mathbf{r}) \psi(\mathbf{r}) d^{3} \mathbf{r}\)(2.31)

Tenga en cuenta que el valor de expectativa depende de la función de onda, i.e del estado físico del sistema, en el que se miden las cantidades. El valor de expectativa general de una cantidad mensurable,\(\hat{A}\) (que a veces se denomina observable), se define como,

\(\langle\hat{A}\rangle_{\psi}=\int \psi^{*}(\mathbf{r}) \hat{A} \psi(\mathbf{r}) d^{3} \mathbf{r}\)(2.32)

donde (\ hat {A}\) es el operador correspondiente a la cantidad física. Un operador en el presente contexto es una operación que transforma una función integrable cuadrada en otra función. Según (2.29) el\(\hat{X}\) operador correspondiente a la coordenada multiplica la función de onda con la coordenada x.

\(\hat{X} \Psi(x, t)=x \Psi(x, t)\)(2.33)

O más generalmente en tres dimensiones:

\(\hat{\mathbf{R}} \Psi(\mathbf{r}, t)=\mathbf{r} \Psi(\mathbf{r}, t)\)(2.34)

Podemos plantear la pregunta, cuál es el operador de la otra cantidad fundamental, el impulso\(\mathbf{p}\). Resulta que el operador correspondiente es el derivado de\(ψ\) multiplicado por el factor\(\frac{\hbar}{i}\), o equivalentemente por\(−iℏ\):

\(\hat{P}_{x} \Psi(x, t)=-i \hbar \frac{\partial}{\partial x} \Psi(x, t)\)(2.35)

\(\hat{\mathbf{P}} \Psi(\mathbf{r}, t)=-i \hbar \nabla \Psi(\mathbf{r}, t)\)(2.36)

Entonces según la regla general 2.32 tenemos en una dimensión

\(\left\langle\hat{P}_{x}\right\rangle_{\psi}=-i \hbar \int \psi^{*}(x) \frac{\partial}{\partial x} \psi(x) d x\)(2.37)

Una justificación de esta afirmación se deja a la siguiente serie de problemas

Problema 2.6

Usando la ecuación de Schrödinger 2.2 demostrar que con las definiciones anteriores se tiene (en una dimensión)

\(\left\langle\hat{P}_{x}\right\rangle_{\psi}=m \frac{d}{d t}\langle\hat{X}\rangle_{\psi}\)(2.38)

Consejos:

• Mostrar que la derivada de tiempo del valor de expectativa de la coordenada puede calcularse como

\(\frac{d}{d t}\langle\hat{X}\rangle=\frac{\hbar}{2 i m} \int\left(\frac{\partial^{2} \Psi^{*}(x, t)}{\partial x^{2}} x \Psi(x, t)-\Psi^{*}(x, t) x \frac{\partial^{2} \Psi(x, t)}{\partial x^{2}}\right) d x\)(2.39)

• Reescribir el integrando como\(\frac{\partial}{\partial x}\left(\frac{\partial \Psi}{\partial x}^{*} x \Psi-\Psi^{*} x \frac{\partial \Psi}{\partial x}-|\Psi|^{2}\right)+2 \Psi^{*} \frac{\partial \Psi}{\partial x}\), y asumiendo que\(Ψ(x,t)\) va a cero en\(±∞\) argumentar que sólo el último término contribuye al resultado.

Problema 2.7

Demostrar que el valor de expectativa de\(\langle\hat{P}\rangle\) es real.

Problema 2.8

Un operador\(\hat{A}\) se llama autoadjoint o (hermitiano) si la siguiente propiedad se mantiene para funciones integrables cuadradas\(φ(\mathbf{r})\) y\(ψ(\mathbf{r})\)

\(\int \varphi^{*}(\mathbf{r})[\hat{A} \psi(\mathbf{r})] d^{3} \mathbf{r}=\int[\hat{A} \varphi(\mathbf{r})]^{*} \psi(\mathbf{r}) d^{3} \mathbf{r}\)(2.40)

Demostrar que los componentes de\(\hat{\mathbf{R}}\) y\(\hat{\mathbf{P}}\) son autoadjoint.

Problema 2.9

Demostrar que el valor de expectativa de un operador autoadjoint es real.

No conmutatividad de\(\hat{X}\) y\(\hat{P}\) operadores

El hecho de que en la mecánica cuántica la coordenada y el impulso estén representados por operadores —y tienen la forma que hemos dado anteriormente— implica que su acción sobre una función de onda\(Ψ(\mathbf{r},t)\) dará resultado diferente si actúan sobre ella en un orden diferente:

\(\hat{X} \hat{P}_{x} \Psi(\mathbf{r}, t)-\hat{P}_{x} \hat{X} \Psi(\mathbf{r}, t)=-i \hbar x \frac{\partial}{\partial x} \Psi(\mathbf{r}, t)+i \hbar \frac{\partial}{\partial x}[x \Psi(\mathbf{r}, t)]=i \hbar \Psi(\mathbf{r}, t)\)(2.41)

o escrito de otra manera:

\((\hat{X} \hat{P}-\hat{P} \hat{X}) \Psi(\mathbf{r}, t)=i \hbar \Psi(\mathbf{r}, t)\)(2.42)

para cualquier función. Esto significa que la acción de los dos operadores es diferente, si se toman en el orden inverso, por lo que este par de operadores es no conmutativo. Se ve fácilmente, que lo mismo es cierto para Y y\(\hat{P}_{y}\) y para\(\hat{Z}\) y\(\hat{P}_{z}\), mientras decir\(\hat{X}\) y\(\hat{P}_{y}\) hacer conmutar, porque la derivación parcial por y da cero para x. De igual manera los componentes de\(\hat{\mathbf{R}}\) entre ellos, así como los componentes de\(\hat{\mathbf{P}}\) entre ellos, se desplazan entre sí. Introduciendo la notación

\(\hat{X} \hat{P}_{x}-\hat{P}_{x} \hat{X}=:\left[\hat{X}, \hat{P}_{x}\right]\)(2.43)

que se llama el conmutador de los operadores\(\hat{X}\) y\(\hat{P}_{x}\), vemos que el conmutador se desvanece si los operadores conmutan, y es distinto de cero si este no es el caso. Para resumir escribimos aquí las siguientes relaciones canónicas de conmutación:

\(\left[\hat{X}_{i}, \hat{X}_{j}\right]=0, \quad\left[\hat{P}_{i}, \hat{P}_{j}\right]=0, \quad\left[\hat{X}_{i}, \hat{P}_{j}\right]=i \hbar \delta_{i j}\)(2.44)

A partir de los operadores de la coordenada y el impulso podemos construir otros operadores dependiendo de estas cantidades. La regla es que en la expresión clásica de una función de\(\mathbf{r}\) y las\(\mathbf{p}\) sustituimos por los operadores correspondientes. Veremos, por ejemplo\(\hat{\mathbf{L}}=\hat{\mathbf{R}} \times \hat{\mathbf{P}}=-i \hbar \mathbf{r} \times \nabla\), que el operador del momento angular orbital y el operador de energía en un sistema conservador están\(\hat{H}=\frac{\hat{\mathbf{p}}^{2}}{2 m}+V(\hat{\mathbf{R}})=-\frac{\hbar^{2}}{2 m} \Delta+V(r)\) de acuerdo con la definición dada en (2.4)

Animación

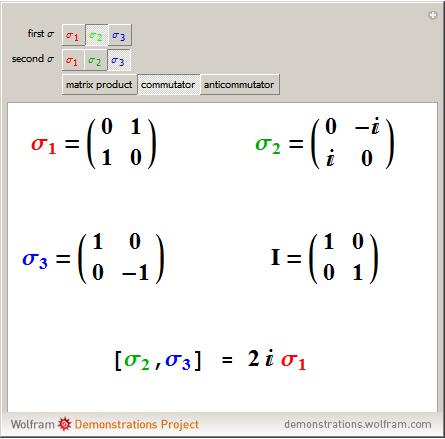
La no conmutatividad surge también en caso de multiplicación matricial. Esta demostración muestra la no conmutatividad en el caso de matrices complejas especiales de 2×22×2, las llamadas matrices Pauli.

http://demonstrations.wolfram.com/PauliSpinMatrices/

Varianza de un operador

Hay un número importante que caracteriza una distribución de probabilidad, que es la propiedad que muestra cuán nítida es la distribución. Se puede obtener una medida de esta propiedad, si tomamos los valores medidos de la variable aleatoria en cuestión, y consideramos un valor medio de ciertas diferencias entre los valores medidos y el valor de expectativa. Como ejemplo volvemos a considerar la coordenada unidimensional x. Tomando el valor de expectativa de las diferencias simples entre los valores medidos y la expectativa no arroja información, ya que esto da cero en los casos de todas las distribuciones posibles debido a la identidad:\(\int_{-\infty}^{\infty}\left[x^{\prime}-\int_{-\infty}^{\infty} x|\psi(x)|^{2} d x\right]\left|\psi\left(x^{\prime}\right)\right|^{2} d x^{\prime}=0\). Una buena medida es, pues, tomar el valor esperado del cuadrado de las diferencias del valor esperado, es decir, la cantidad:

\((\Delta \hat{X})_{\psi}^{2}:=\int_{-\infty}^{\infty}\left[x^{\prime}-\int_{-\infty}^{\infty} x|\psi(x)|^{2} d x\right]^{2}\left|\psi\left(x^{\prime}\right)\right|^{2} d x^{\prime}\)(2.45)

que se denomina varianza de x, y que es la definición habitual en la teoría de probabilidad, con una densidad de probabilidad\(|\psi(x)|^{2}=\rho(x)\). También llamaremos a esto la varianza del operador\(\hat{X}\) en el estado\(ψ\). Esta última terminología se debe a la reformulación de la definición anterior como:

\((\Delta \hat{X})_{\psi}^{2}=\left\langle\left(\hat{X}-\langle\hat{X}\rangle_{\psi}\right)^{2}\right\rangle_{\psi}\)(2.46)

o en general para cualquier operador lineal y autoadjoint (2.32).

\((\Delta \hat{A})_{\psi}^{2}=\left\langle\left(\hat{A}-\langle\hat{A}\rangle_{\psi}\right)^{2}\right\rangle_{\psi}\)(2.47)

La varianza también se llama el segundo momento central de la distribución de probabilidad. La raíz cuadrada\(\sqrt{(\Delta \hat{A})_{\psi}^{2}}=:(\Delta \hat{A})_{\psi}\) se llama la raíz media cuadrada desviación de la cantidad física\(\hat{A}\) en el estado dado por\(ψ\). Podemos reescribir esta fórmula de dos maneras distintas. Primero simplemente se ve que

\((\Delta \hat{A})_{\psi}^{2}=\left\langle\hat{A}^{2}-2 \hat{A}\langle\hat{A}\rangle_{\psi}+\langle\hat{A}\rangle_{\psi}^{2}\right\rangle_{\psi}=\left\langle\hat{A}^{2}\right\rangle_{\psi}-\langle\hat{A}\rangle_{\psi}^{2}\)(2.48)

porque\ (\ langle\ hat {A}\ rangle_ {\ psi}/) ya es un número. Sigue una declaración importante si escribimos

\ (\ begin {alineado}
(\ Delta\ hat {A}) _ {\ psi} ^ {2} &=\ izquierda\ langle\ izquierda (\ hat {A} -\ langle\ hat {A}\ rangle_ {\ psi}\ derecha) ^ {2}\ derecha\ rangle_ {\ psi} =\ int\ psi^ {*} (\ mathbf {r})\ izquierda (\ hat {A} -\ langle\ hat {A}\ rangle_ {\ psi}\ derecha) ^ {2}\ psi (\ mathbf {r}) d^ {3}\ mathbf {r} =\\
&\ izquierda. =\ int\ izquierda [\ izquierda (\ hat {A} -\ langle\ hat {A}\ rangle_ {\ psi}\ derecha)\ psi (\ mathbf {r})\ derecha] ^ {*}\ izquierda [\ izquierda (\ hat {A} -\ langle\ hat {A}\ rangle_ {\ psi}\ derecha)\ psi (\ mathbf {r}) derecha\] d^ {3}\ mathbf {r} =\ int\ mid\ hat {A} -\ langle\ hat {A}\ rangle_ {\ psi}\ psi (\ mathbf {r})\ derecha)\ izquierda. \ derecha|^ {2} d^ {3}\ mathbf {r}
\ end {alineado}\) (2.49)

Con base en esta fórmula, simplemente podemos responder a la pregunta: ¿qué tipo de funciones de onda son esas, dónde podemos medir la cantidad correspondiente\(\hat{A}\) con varianza cero, es decir, con un valor que siempre es el mismo? Para tener\((\Delta \hat{A})_{\psi}^{2}=0\) la integral en la última expresión debe ser cero. Pero como es una integral de un valor absoluto cuadrado que no es negativo en todas partes, puede ser cero si y solo si\(\left(\hat{A}-\langle\hat{A}\rangle_{\psi}\right) \psi(\mathbf{r})=0\), o dicho lo contrario, si y solo si

\(\hat{A} \psi(\mathbf{r})=\langle\hat{A}\rangle_{\psi} \psi(\mathbf{r})\)(2.50)

Cualquier función que obedezca esta ecuación se llama la función propia del operador\(\hat{A}\). En la forma anterior esta ecuación sólo tiene una significación principal y en la mayoría de los casos conociendo al operador, no se conocen a priori las funciones propias. Por lo tanto, el problema suele ser determinar los valores propios y las funciones propias de\(\hat{A}\) a partir de la ecuación:

\(\hat{A} \varphi(\mathbf{r})=\alpha \varphi(\mathbf{r})\)(2.51)

Este fue el caso anterior, en particular, para el operador de Hamilton en (2.12).

Problema 2.10

Demostrar que el valor de expectativa de\(\hat{A}\) en el estado dado por el normalizado\(φ(r)\), es apenas α.

Un teorema importante muestra que el producto de varianzas de dos operadores que no se desplazan tiene un límite inferior, el cual es generalmente positivo. En el caso de los operadores de coordenadas e impulso toma la forma

\((\Delta \hat{X})_{\psi} \cdot\left(\Delta \hat{P}_{x}\right)_{\psi} \geq \frac{\hbar}{2}\)(2.52)

para cualquier función de onda\(ψ\), y una desigualdad similar se mantiene para los otros dos\((y,z)\) componentes. Aquí no se dará la prueba matemática de la desigualdad, que habitualmente se denomina relación de incertidumbre de Heisenberg