7: Estructura molecular y espectros

Objetivos

En este capítulo discutiremos la cuestión sobre la estructura interna y la energía de las moléculas, que dependen no sólo de la distribución de los electrones como en los átomos, sino también de la ubicación y movimiento de los núcleos atómicos. Si bien los diferentes mecanismos posibles responsables de los espectros moleculares están interrelacionados, existen tres tipos de movimientos que se pueden distinguir en la práctica, ya que las diferencias en sus energías típicas permiten que su caracterización sea examinada de manera independiente. Los tres mecanismos principales que determinan los espectros de las moléculas son sus excitaciones electrónicas, vibracionales y rotacionales.

Prerrequisitos

Capítulos 2, 4-5-6. Moléculas y valencia en química. Rotación de cuerpos rígidos, el oscilador armónico.

Introducción

Por simplicidad, y para captar la esencia de este tema, consideraremos moléculas diatómicas. En particular, la interacción entre dos átomos neutros y su dependencia de su distancia RR entre sí nos dará una mejor visión de la naturaleza del enlace químico. Además, el modelo de orbitales atómicos, que da una imagen intuitiva de la distribución espacial de electrones y juega un papel importante en la química, puede explicarse más fácilmente para las moléculas diatómicas. Dado que los niveles de energía de las moléculas no solo están determinados por la excitación electrónica sino también por las vibraciones de los núcleos, o la rotación de toda la molécula alrededor de un eje a través de su centro de masa, los espectros de las moléculas son mucho más complejos que los de los átomos, pero por otro lado también dan más información detallada sobre la estructura interna y la dinámica de las moléculas. Primero llegamos a la discusión más simple de los estados electrónicos, y explicamos por qué dos átomos neutros tienden a formar una molécula.

Orbitales moleculares de moléculas diatómicas.

Consideraremos un problema específico, la\(\mathrm{H}_{2}\) molécula neutra, donde también está presente la interacción electrón-electrón, y este ejemplo explica también por qué dos átomos de H eléctricamente neutros tienden a formar una molécula estable, en lugar de permanecer separados. Este es el problema de larga data de la valencia, que sólo puede explicarse por la teoría cuántica. Al considerar la\(\mathrm{H}_{2}\) molécula asumiremos en esta sección que los dos protones están en posiciones fijas en el espacio, e intentaremos determinar la función de onda de dos electrones del sistema en su estado fundamental. La energía resultante dependerá de la distancia entre los núcleos, y luego la dinámica de ese grado de libertad puede investigarse más a fondo.

Figura 7.1:\(\mathrmH_{2}\) molécula.

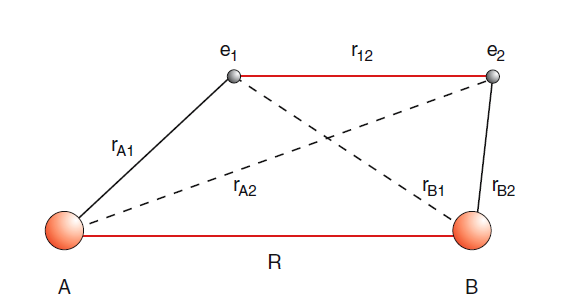
El hamiltoniano del sistema, que no contiene movimiento nuclear (con\(e_{0}^{2}=q_{0}^{2} / 4 \pi \epsilon_{0}\)) es

\(H=\frac{P_{1}^{2}}{2 m}+\frac{P_{2}^{2}}{2 m}-\frac{e_{0}^{2}}{\left|\mathbf{R}_{1}-\mathbf{R}_{A}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{R}_{1}-\mathbf{R}_{B}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{R}_{2}-\mathbf{R}_{A}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{R}_{2}-\mathbf{R}_{B}\right|}+\frac{e_{0}^{2}}{\left|\mathbf{R}_{1}-\mathbf{R}_{2}\right|}+\frac{e_{0}^{2}}{R}\)(7.1)

Problema 7.1

Explique los términos en este hamiltoniano.

Uno de los métodos para encontrar los valores propios de la energía es el siguiente. Tratamos de construir una función de onda molecular, llamada orbital molecular como combinación lineal de orbitales atómicos, abreviada como el método MO LCAO. Supongamos que en el estado fundamental de la molécula el orbital molecular de uno de los electrones puede escribirse como la combinación lineal de orbitales hidrogénicos de estado\(1s\) fundamental normalizados, que están centrados en las posiciones nucleares:

\(\phi(\mathbf{r})=c_{A} \phi_{A}(\mathbf{r})+c_{B} \phi_{B}(\mathbf{r})\)(7.2)

donde

\(\phi_{A}(\mathbf{r})=\frac{1}{\sqrt{\pi a_{0}^{3}}} e^{-\left(\mathbf{r}-\mathbf{R}_{A}\right) / a_{0}}, \quad \phi_{B}(\mathbf{r})=\frac{1}{\sqrt{\pi a_{0}^{3}}} e^{-\left(\mathbf{r}-\mathbf{R}_{B}\right) / a_{0}}\)(7.3)

Debido a la simetría del problema elegimos\(c_{B}=±c_{A}\) cuál lleva después de la normalización a las siguientes dos funciones de onda para un solo electrón en el campo de los dos núcleos:

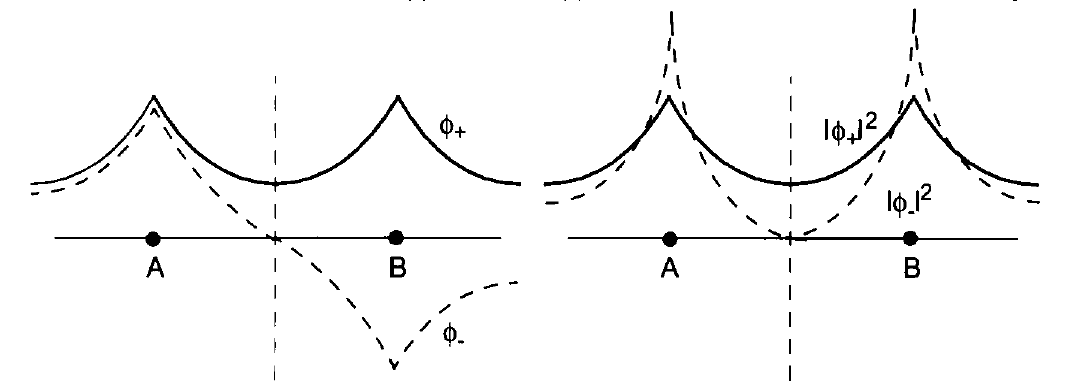
\(\phi_{+}(\mathbf{r})=\frac{\phi_{A}(\mathbf{r})+\phi_{B}(\mathbf{r})}{\sqrt{2+2 S(R)}} \quad \phi_{-}(\mathbf{r})=\frac{\phi_{A}(\mathbf{r})-\phi_{B}(\mathbf{r})}{\sqrt{2-2 S(R)}}\)(7.4)

donde\(S(R):=\int \phi_{A}^{*}(\mathbf{r}) \phi_{B}(\mathbf{r}) d^{3} \mathbf{r}\) es una constante real, ya que las\(1s\) funciones anteriores son reales. \(S(R)\)se llama la integral de superposición de las funciones centradas en los dos núcleos. Será una función de la distancia\(R=|\mathbf{R}_{A}−\mathbf{R}_{B}|\) entre los núcleos, y va disminuyendo con el aumento de R. Obsérvese que\(ϕ_{+}(\mathbf{r})\) en (7.4)\(ϕ_{−}(\mathbf{r})\) es un simétrico mientras que es una función antisimétrica con respecto al intercambio de los dos núcleos idénticos. A continuación se discutirá la cuestión de cuál de los dos se va a utilizar para describir los electrones, cuando también se debe tomar en cuenta el espín electrónico.

Figura 7.2: Ondas y su valor absoluto cuadrado para un solo electrón en el campo de los dos núcleos. Ver Eqn. (7.4).

Ahora asumimos que cada uno de los dos electrones está en uno de los estados\(ϕ_{+}(\mathbf{r})\), o\(ϕ_{−}(\mathbf{r})\) arriba, y buscamos la función de onda de dos partículas como su producto.

El estado singlete

Primero consideramos la posibilidad, cuando ambos electrones están en los\(ϕ_{+}(\mathbf{r})\) estados:

\(\psi_{s}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\phi_{+}\left(\mathbf{r}_{1}\right) \phi_{+}\left(\mathbf{r}_{2}\right)\)(7.5)

Obviamente esto es simétrico con respecto al intercambio de los dos electrones, y por lo tanto según el postulado que requiere la antisimetría de las funciones de onda para los fermiones, no puede ser una función de onda verdadera. Pero como sabemos, este no es el estado total, porque los electrones poseen un grado de libertad de espín, que —aunque no está contenido en el hamiltoniano— influye en las propiedades de simetría del estado. Podemos completar la función de onda espacial simétrica mediante una parte de espín antisimétrica formando el determinante Slater:

\ (\ psi_ {s}\ izquierda (\ mathbf {r} _ {1}, m_ {1},\ mathbf {r} _ {2}, m_ {2}\ derecha) =\ frac {1} {\ sqrt {2}}\ izquierda|\ begin {array} {ll}
\ phi_ {+}\ izquierda (\ mathbf {r} _ {1}\ derecha)\ chi^ {+} (1) &\ phi_ {+}\ izquierda (\ mathbf {r} _ {2}\ derecha)\ chi^ {+} (2)\\
\ phi_ {+}\ izquierda (\ mathbf {r} _ {1}\ derecha)\ chi^ {-} (1) &\ phi_ {+}\ izquierda (\ mathbf {r} _ {2}\ derecha)\ chi^ {-} (2)
\ end {array}\ derecha|\) (7.6)

donde\(χ^{+}(i)\) y\(χ^{−}(i)\) son los dos estados propios diferentes y ortogonales del\(S_{z}\) operador (spin up\(+\), spin down\(−\), según el uso común (5.2)) para la i-ésima partícula.

Al expandir el determinante obtenemos

\ (\ begin {alineado}
&\ psi_ {s}\ izquierda (\ mathbf {r} _ {1}, m_ {1},\ mathbf {r} _ {2}, m_ {2}\ derecha) =\ frac {1} {\ sqrt {2}}\ phi_ {+}\ izquierda (\ mathbf {r} _ {1}\ derecha)\ phi_ {+}\ izquierda (\ mathbf {r} _ {2}\ derecha)\ izquierda\ {\ chi^ {+} (1)\ chi^ {-} (2) -\ chi^ {+} (2)\ chi^ {-} (1)\ derecha\} =\
&=\ frac {1} {2\ sqrt {1+S (R)}}\ izquierda\ { \ phi_ {A}\ izquierda (\ mathbf {r} _ {1}\ derecha) +\ phi_ {B}\ izquierda (\ mathbf {r} _ {1}\ derecha)\ derecha\}\ izquierda\ {\ phi_ {A}\ izquierda (\ mathbf {r} _ _ {2}\ derecha) +\ phi_ {B}\ izquierda (\ mathbf {r} _ {2}\ derecha)\ derecha\}\ izquierda\ {\ chi^ {+} (1)\ chi^ {-} (2) -\ chi^ {+} (2)\ chi^ {-} (1)\ derecha\}
\ final {alineada}\) (7.7)

En vista de lo último, factor dependiente de espín en (7.7) uno a veces simplemente dice que en este estado los dos electrones tienen espines antiparalelos. Como el estado de giro antisimétrico\(\left\{\chi^{+}(1) \chi^{-}(2)-\chi^{+}(2) \chi^{-}(1)\right\} / \sqrt{2}\) se llama singlete de giro, la afirmación más correcta es que el\(ψ_{s}\) estado total es un estado singlete de giro.

El estado triplete

A partir de (7.4) también podemos construir una función de onda espacial que es antisimétrica con respecto al intercambio de los electrones. A diferencia de lo simétrico\(ψ_{s}\) tomamos la combinación

\(\psi_{a}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\frac{1}{\sqrt{2}}\left\{\phi_{+}\left(\mathbf{r}_{1}\right) \phi_{-}\left(\mathbf{r}_{2}\right)-\phi_{-}\left(\mathbf{r}_{1}\right) \phi_{+}\left(\mathbf{r}_{2}\right)\right\}\)(7.8)

que es antisimétrico si cambiamos los electrones. Esto debe ser nuevamente completado por partes dependientes del giro, que deben ser entonces simétricas, de manera que el estado total sea antisimétrico. Hay tres funciones de espín simétricas diferentes y ortogonales de las dos partículas, que son las siguientes:

\(\chi^{+}(1) \chi^{+}(2), \quad \frac{1}{\sqrt{2}}\left\{\chi^{+}(1) \chi^{-}(2)+\chi^{-}(1) \chi^{+}(2)\right\}, \quad \chi^{-}(1) \chi^{-}(2)\)(7.9)

Multiplicando\(ψ_a\) con cualquiera de estos obtenemos nuevamente una función de onda permitida\(\psi_{a}\left(\mathbf{r}_{1}, m_{1}, \mathbf{r}_{2}, m_{2}\right)\). Uno dice vagamente, que los dos giros son paralelos en estos estados. Como hay tres de ellos, llamamos a estos tres estados de giro, así como a la función de onda total como triplete.

Problema 7.3

Multiplique\(ψa\) por el segundo de estos estados de giro simétricos y escriba el resultado como determinante de Slater.

Los valores de expectativa energética de los estados

Ahora se pueden encontrar las energías en los estados\(ψ_{s}\) y\(ψ_{a}\) calculando\(\varepsilon_{s}=\int \psi_{s}^{*} H \psi_{s} d^{3} \mathbf{r}_{1} d^{3} \mathbf{r}_{2}\) y\(\varepsilon_{a}=\int \psi_{a}^{*} H \psi_{a} d^{3} \mathbf{r}_{1} d^{3} \mathbf{r}_{2}\), donde H es el operador Hamilton (7.1). En los cálculos aparece la energía del estado fundamental\(ε_{1}\) de un H aislado:\(\frac{P_{i}^{2}}{2 m}-\frac{e_{0}^{2}}{\left|R_{i}-R_{A(B)}\right|}\). Además el resultado contendrá la energía Coulomb

\(Q=\int \phi_{A}^{2}\left(\mathbf{r}_{1}\right) \phi_{B}^{2}\left(\mathbf{r}_{2}\right)\left(\frac{e_{0}^{2}}{\left|\mathbf{r}_{1}-\mathbf{r}_{2}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{r}_{1}-R_{B}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{r}_{2}-R_{A}\right|}\right) d^{3} \mathbf{r}_{1} d^{3} \mathbf{r}_{2}+\frac{e_{0}^{2}}{R}\)(7.10)

y la llamada energía de intercambio A:

\(A=\int \phi_{A}\left(\mathbf{r}_{1}\right) \phi_{B}\left(\mathbf{r}_{2}\right) \phi_{A}\left(\mathbf{r}_{2}\right) \phi_{B}\left(\mathbf{r}_{1}\right)\left(\frac{e_{0}^{2}}{\left|\mathbf{r}_{1}-\mathbf{r}_{2}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{r}_{1}-R_{B}\right|}-\frac{e_{0}^{2}}{\left|\mathbf{r}_{2}-R_{A}\right|}\right) d^{3} \mathbf{r}_{1} d^{3} \mathbf{r}_{2}+S^{2}(R) \frac{e_{0}^{2}}{R}\)(7.11)

que es la medida de la superposición de las dos funciones de onda electrónica ponderadas por la energía potencial, y resulta de la interacción del principio Pauli y la interacción de Coulomb. El resultado es

\(\varepsilon_{s}=2 \varepsilon_{1}+\frac{Q+A}{1+S^{2}}, \quad \varepsilon_{a}=2 \varepsilon_{1}+\frac{Q-A}{1-S^{2}}\)(7.12)

Aquí tanto Q como A dependen de la distancia nuclear R. La energía de Coulomb Q es positiva, mientras que aparte de muy pequeña R -s A es negativa y\(|A|>Q\). Esto da como resultado la dependencia de los valores energéticos de εsεs como se muestra en la Fig. 7.3

Figura 7.3: Dependencia de los valores de energía\(ε_{s}\) de la distancia nuclear R.

Esto significa que el estado singlete (espines antiparalelos en el sentido del último factor en (7.7)) es estable alrededor de una distancia de equilibrio\(R=R_{e}\). El valor calculado a partir de este modelo simple es\(R_{e}=0.8\mathrm{nm}\), mientras que el valor medido es\(0.74\mathrm{nm}\). El estado\(ψ_{s}\) se llama por lo tanto un estado de unión, y se denota por\(σ\). El otro, el estado triplete, que es antisimétrico en el espacio pero los espines de los dos electrones son paralelos en el sentido de (7.9) no es estable, no hay mínimo en la energía, se le llama estado antienlace, y se denota por\(σ^{∗}\). Consulte la figura 7.4 y la animación a continuación.

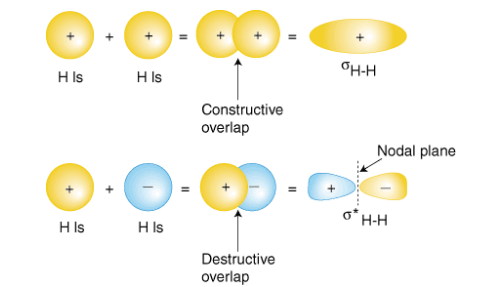
Figura 7.4: Dibujo esquemático de estados de unión y antiadhesión.
http://www.sparknotes.com/chemistry/bonding/molecularorbital/section1.rhtml

Nota

Se muestran los orbitales moleculares (MO) de unión y antiunión de menor energía para una molécula homonuclear diatómica, ya que se varía la distancia internuclear. Los contornos rojos designan valores negativos de la función de onda.

http://demonstrations.wolfram.com/BondingAndAntibondingMolecularOrbitals/

La\(\mathrm{H}_{2}\) molécula es una molécula diatómica homonuclear, donde homonuclear significa que los dos núcleos son idénticos. En algunas de las moléculas diatómicas heteronucleares (diferentes átomos) hay otro efecto además del que discutimos aquí. En HCl por ejemplo la nube de electrones será asimétrica a lo largo del eje molecular, el electrón del átomo de H tiende a acercarse al Cl y simplemente la atracción del protón por el ion Cl cargado negativamente estabilizará esta molécula.

El ejemplo que consideramos anteriormente fue uno de los más simples. El cálculo de la estructura electrónica de grandes moléculas muy complicadas se ha hecho posible en la segunda mitad del siglo XX debido al desarrollo técnico de computadoras electrónicas rápidas, así como a la evolución de sofisticados algoritmos y paquetes de programas, que son los tema de la ciencia llamada química cuántica.

Espectros moleculares

En el sistema atómico, nuestra consideración de las transiciones radiativas se limitó al problema de las transiciones electrónicas entre estados. En las moléculas, la estructura interna permite también transiciones que involucran excitaciones rotacionales y vibracionales de los núcleos constituyentes. Al igual que con los átomos, las transiciones electrónicas son típicamente del orden de eV, correspondientes a longitudes de onda en o cerca de la región óptica. Sin embargo, es poco probable que ocurra una transición electrónica sin inducir el movimiento de los núcleos, también, debido a que las distancias de equilibrio entre los núcleos serán diferentes en los estados electrónicos inicial y final. Las energías típicas de los estados rotacionales de las moléculas son mucho más pequeñas que las de los estados electrónicos excitados\(ℏ^{2}/2Θ\), de orden, donde\(Θ\) está el momento molecular de inercia. Sustituyendo valores típicos por el espaciado interatómico y las masas atómicas, se encuentra que las energías rotacionales son del orden\(10^{-4} \mathrm{eV}\) correspondiente a las regiones de infrarrojo lejano o microondas. Las energías típicas para las excitaciones vibracionales de las moléculas están alrededor\(10^{-1} \mathrm\{eV}\) correspondientes a la banda de onda infrarroja. Todos estos tipos de transiciones pueden ocurrir radiativamente, es decir, a través de la emisión o absorción de un fotón de la frecuencia apropiada\(ν=Δε/h\). Como en el caso de los átomos, las transiciones radiativas más probables suelen ser las transiciones dipolares eléctricas. En una transición dipolar eléctrica, el fotón se lleva o trae una unidad de momento angular y paridad negativa, por lo que habrá la regla de selección habitual para el cambio en el número cuántico de momento angular total de la molécula:\(ΔJ=0,±1\), pero no\(0→0\), acompañado de un cambio en la paridad de el estado molecular (que puede imponer restricciones adicionales\(ΔJ\)).

Figura 7.5: Esta figura visualiza la diferencia en órdenes de magnitud para los diferentes tipos de transiciones (electrónica, vibracional y rotacional).
http://hyperphysics.phy-astr.gsu.edu/hbase/molecule/molec.html

En un gas o un líquido, las transiciones también pueden producirse por colisiones entre sus moléculas. El cambio de energía apropiado puede ser proporcionado por excitación o desexcitación de la otra molécula, o como parte de la energía cinética de la colisión. Dichas transiciones no radiativas no tienen que obedecer las reglas de selección anteriores. Así, por ejemplo, una molécula en un estado metaestable, es decir, una que no puede regresar al estado fundamental a través de una transición radiativa permitida, puede ser desexcitada por una colisión. En ausencia de cualquier radiación incidente u otras fuentes de excitación no térmicas, las colisiones provocarán una distribución térmica de los niveles de energía molecular, con el número de moléculas en estado ii dado por\(\), dónde\(g_{i}\) está la degeneración y\(ε_{i}\) la energía. A temperatura ambiente\(k_{B}T=2×10^{−2}\mathrm{eV}\), por lo que normalmente muchos estados rotacionales de las moléculas están excitados, pero no electrónicos o vibracionales.

En una molécula giratoria y vibrante la energía cinética de los núcleos es pequeña comparada con la energía del estado molecular. Esto se debe a que las masas nucleares son grandes, y por lo tanto su movimiento es lento en comparación con el movimiento de los electrones. Esto permite la separación de la función de onda total\(Φ(\mathbf{R,r})\) en un producto\(Φ(\mathbf{R,r})=ϕ(\mathbf{R})ψ(\mathbf{R,r})\) de una función de onda nuclear\(ϕ(\mathbf{R})\) y una función electrónica\(ψ(\mathbf{R,r})\) que depende de las coordenadas electrónicas\(\mathbf{r}\) y contiene las posiciones nucleares\(\mathbf{R}\) como parámetros. Esta aproximación se denomina aproximación adiabática o Born-Oppenheimer. Dentro de esta aproximación la energía total de un nivel molecular puede escribirse como una suma de las energías electrónica, vibracional y rotacional.

Animación

Aquí se muestra el movimiento térmico de un segmento de la hélice alfa de la proteína. Las moléculas tienen diversos grados de libertad vibracional y rotacional internos. Esto se debe a que las moléculas son objetos complejos; son una población de átomos que pueden moverse dentro de una molécula de diferentes maneras. Esto hace que las moléculas sean distintas de los gases nobles como el helio y el argón, que son monatómicos (que consisten en átomos individuales).

http://upload.wikimedia.org/Wikipedia/commons/2/23/Thermally_Agitated_Molecule.gif

Rotación molecular

El modelo de una molécula diatómica rígida

En general, la ecuación de Schrödinger para el movimiento nuclear tiene muchas soluciones, que dan los diversos niveles de energía molecular para una configuración electrónica dada. El caso más sencillo es el de una molécula diatómica donde la molécula puede caracterizarse por su momento de inercia con respecto a su centro de masa. Si asumimos en la primera aproximación que la molécula es rígida, y consideramos el problema en el sistema fijado al centro de masa de la molécula, entonces se puede separar la energía cinética traslacional. Desde el punto de vista de las rotaciones, la molécula se caracteriza por su momento de inercia\(\Theta=\mu r_{0}^{2}\) alrededor de un eje a través del centro de masa ortogonal al enlace, donde\(r_{0}\) está la longitud del enlace de equilibrio, y\(μ\) es la masa reducida de los dos átomos. La energía cinética rotacional se puede expresar por el momento angular\(\mathcal{L}=Θω\) como

\(\frac{1}{2} \Theta \omega^{2}=\frac{\mathcal{L}^{2}}{2 \Theta}\)(7.13)

y si reemplazamos el clásico\(\mathcal{L}\) por el operador del momento angular obtenemos el operador Hamilton del movimiento rotacional puro:

\(H=\frac{L^{2}}{2 \Theta}\)(7.14)

Los estados estacionarios son las soluciones de la ecuación de valor propio

\(\frac{L^{2}}{2 \Theta} \Phi=\varepsilon_{J} \Phi\)(7.15)

Como\(L^{2}\) es un cuadrado de un momento angular perteneciente a un movimiento orbital sus valores propios son de la forma\(ℏ^{2}J(J+1)\), (en espectroscopia molecular en lugar de la notación\(ℓ\), usamos\(J\)) donde\(J=0,1, \ldots\), y su proyección\(m_{J}\) toma los valores\(J, J-1, \ldots,-J\)). Por lo tanto, los valores propios de la energía rotacional son

\(\varepsilon_{J}=\frac{\hbar^{2}}{2 \Theta} J(J+1)\)(7.16)

mientras que las funciones propias serán las funciones armónicas esféricas\(\Phi=Y_{J}^{m_{J}}\). Como se mencionó anteriormente, las energías típicas de los estados rotacionales de las moléculas son mucho más pequeñas que las de los estados electrónicos excitados. Dado que las dimensiones moleculares están determinadas por la función de onda electrónica, su escala se establece por el radio de Bohr\(a_{0}\). Así, los momentos de inercia son de orden\(m_{N} a_{0}^{2}\) y la escala de las energías rotacionales lo es\(\hbar^{2} / m_{N} a_{0}^{2}\). Para los estados electrónicos, la desigualdad de Heisenberg implica momentos de orden\(\hbar / a_{0}\) y por lo tanto energías electrónicas alrededor\(\hbar^{2} /\left(m_{e} a_{0}^{2}\right)\), un factor de\(m_{N} / m_{e} \simeq 10^{4}\) mayor. Para lograr una transición rotacional radiativa, un fotón emitido o absorbido debe interactuar con el momento dipolar eléctrico de la molécula. En una transición rotacional pura los estados electrónicos inicial y final son los mismos, por lo tanto el estado necesita tener un momento dipolar eléctrico permanente. Así podemos tener transiciones radiativas puramente rotacionales en moléculas diatómicas heteronucleares como HCl y CO, que tienen momentos dipolares permanentes, pero no en homonucleares como\(\mathrm{H}_{2}\) y\(\mathrm{O}_{2}\).

Se aplican las reglas habituales de selección de dipolos eléctricos:\(ΔJ=±1,0\) con un cambio de paridad. En un estado rotacional con números cuánticos de momento angular\(J\) y\(m_{J}\), la función de onda nuclear es proporcional a la armónica esférica\(Y_{J}^{m_{J}}\), que tiene paridad\((−1)^{J}\). (Por simplicidad, consideramos únicamente los estados moleculares en los que la función de onda electrónica tiene cero momento angular e incluso paridad). Entonces el hecho de que la paridad deba cambiar en una transición radiativa excluye la posibilidad\(ΔJ=0\). Por lo tanto, los posibles cambios energéticos en la emisión (\(J+1⟶J;J=0,1,2\ldots\)) vienen dados por:

\(\Delta \varepsilon=\frac{\hbar^{2}}{2 \Theta}[(J+1)(J+2)-J(J+1)]=\frac{\hbar^{2}}{\Theta}(J+1)\)(7.17)

En consecuencia, se espera que el espectro consista en líneas con frecuencias crecientes.

Para especificar una línea espectral en espectroscopía molecular práctica se utiliza el número de onda\(\bar{\nu}=1 / \lambda=\nu / c\), el cual se obtiene de acuerdo con la regla de Bohr (\(\bar{\nu}=\Delta \varepsilon / h c\)) como diferencia de términos:

\(F_{J}=\frac{\varepsilon_{J}}{h c}\)(7.18)

Aquí la palabra término es la terminología estándar para la expresión en (7.18). Entonces los números de onda correspondientes a las diferencias de energía, es decir, a la transición, se obtienen de (7.17) como:

\(\bar{\nu}_{\mathrm{rot}}(J)=2 B(J+1)\)(7.19)

donde la constante de rotación\(B=\hbar / 4 \pi c \mu R_{e}^{2}\), se expresa aquí con la masa reducida\(μ\). Las transiciones rotacionales caen en el dominio THZ-GHz, es decir, en el rango de infrarrojo lejano o microondas. De hecho, la tasa de emisión espontánea entre estados rotacionales es muy pequeña, debido a la pequeña liberación de energía. La tasa de emisión espontánea varía a medida que\(ω^{3}\), por lo que las transiciones rotacionales se estudian más convenientemente mediante espectroscopia de absorción La misma fórmula para las energías de transición se aplica claramente al caso de\(J⟶(J+1)\) absorción, también. La observación de este espaciamiento se puede utilizar para determinar el momento de inercia y por lo tanto la longitud del enlace de la molécula.

Las intensidades de las líneas espectrales rotacionales muestran algunas características interesantes. Aunque el elemento de la matriz de transición depende de los números cuánticos, el factor dominante suele ser la población del estado inicial. Como se mencionó anteriormente, las transiciones no radiativas debidas a colisiones moleculares producen una distribución térmica,

\(\)(7.20)

Esto aumenta\(J\) hasta con algún valor, que depende de la temperatura, y luego disminuye. Así, las líneas espectrales sucesivas aumentan y luego disminuyen en intensidad.

Distorsión centrífuga

Una molécula real no es rígida. Cuando gira, la fuerza centrífuga actúa sobre los átomos y la distancia internuclear aumenta a un valor R donde esta fuerza\(F_{c}=-M \omega^{2} R\) es compensada por la fuerza restauradora que\(F_{r}=-d E_{p o t}(R) / d R\) mantiene unidos los dos átomos, lo que depende de la pendiente de la función de energía potencial\(E_{pot}(R)\). En las proximidades de la distancia de equilibrio\(R_{e}\) el potencial puede aproximarse mediante una función parabólica. Esto conduce a una fuerza de restauración lineal

\(F_{r}=-k\left(R-R_{e}\right)\)(7.21)

De la relación\(J^{2}=\Theta^{2} \omega^{2}=M^{2} R^{4} \omega^{2}\) obtenemos:

\(M \omega^{2} R=\frac{J(J+1)}{M R^{3}} \hbar^{2}=k\left(R-R_{e}\right)\)(7.22)

lo que lleva a

\(R=R_{e}+\frac{J(J+1) \hbar^{2}}{M k R^{3}}\)(7.23)

Esto significa que la distancia internuclear R se incrementa por la rotación molecular. Dado que la energía potencial\(E_{pot}(R)\) tiene un mínimo para\(R=R_{e}\), en caso de que\(ReqR_{e}\) tengamos una energía adicional\(\Delta E_{p o t}=\frac{k}{2}\left(R-R_{e}\right)^{2}\) en el caso de un rotor no rígido. La energía total del rotor no rígido es entonces

\(\varepsilon_{r o t}=\frac{J(J+1) \hbar^{2}}{M R^{2}}+\frac{1}{2} k\left(R-R_{e}\right)^{2}\)(7.24)

Si expresamos RR en el lado derecho de (7.23) por\(R_{e}\) y k con la ayuda de (7.22) obtenemos

\(R=R_{e}\left(1+\frac{J(J+1) \hbar^{2}}{M k R_{e}^{4}}\right)\)(7.25)

donde se encuentra el segundo término\(≪1\). Esto nos permite expandirnos\(1/R^{2}\) a la serie de potencia

\(\frac{1}{R^{2}}=\frac{1}{R_{e}^{2}}\left(1-\frac{2 J(J+1) \hbar^{2}}{M k R_{e}^{4}}+\frac{3 J^{2}(J+1)^{2} \hbar^{4}}{M^{2} k^{2} R_{e}^{8}} \mp \ldots\right)\)(7.26)

y la energía rotacional llega a ser de tercer orden en\(ℏ^{2}\)

\(\varepsilon_{r o t}=\frac{J(J+1) \hbar^{2}}{2 M R_{e}^{2}}-\frac{J^{2}(J+1)^{2} \hbar^{4}}{2 M^{2} k R_{e}^{6}}+\frac{3 J^{3}(J+1)^{3} \hbar^{6}}{2 M^{3} k^{2} R_{e}^{10}}\)(7.27)

Esto significa que para un valor dado del número cuántico rotacional J la fuerza centrífuga hace que el momento de inercia sea mayor y, por lo tanto, la energía rotacional sea más pequeña. Este efecto sobrecompensa el aumento de la energía potencial.

Usando de nuevo los valores de término en lugar de las energías, (7.27) se convierte

\(F_{r o t}(J)=B_{e} J(J+1)-D_{e} J^{2}(J+1)^{2}+H_{e} J^{3}(J+1)^{3}\)(7.28)

con las constantes rotacionales:

\ (\ F_ {r o t} (J) =B_ {e} J (J+1) -D_ {e} J^ {2} (J+1) ^ {2} +H_ {e} J^ {3} (J+1) ^ {3}) (7.29)

La precisión espectroscópica experimental es hoy en día suficientemente alta para medir incluso la constante de orden superior\(H_{e}\).

Transiciones vibracionales

Aproximación armónica

Otro tipo importante de movimiento molecular es la vibración, en la que los núcleos oscilan alrededor de sus posiciones de equilibrio. Para una molécula diatómica, podemos hacer una expansión Taylor del potencial molecular\(E_{0}(R)\) alrededor de la separación nuclear en equilibrio\(R_{0}\) para obtener

\(E_{0}(R)=E_{0}\left(R_{0}\right)+\left.\frac{1}{2}\left(R-R_{0}\right)^{2} \frac{\partial^{2}}{\partial R^{2}} E_{0}(R)\right|_{R=R_{0}}+\ldots\)(7.30)

El primer derivado se desvanece, porque\(E_{0}(R)\) tiene un mínimo en\(R_{0}\). \(E_{0}(R_{0})\)es una constante, y el segundo término en el lado derecho se puede escribir como\(\), que es el potencial para un oscilador armónico lineal simple con\(X=R−R_{0}\), y frecuencia clásica

\(\omega=\left[\left.\frac{1}{\mu} \frac{\partial^{2}}{\partial R^{2}} E_{0}\right|_{R=R_{0}}\right]^{1 / 2}\)(7.31)

donde\(μ\) está la masa reducida. Según la teoría cuántica del oscilador armónico, los niveles de energía, incluida la vibración nuclear, están dados por

\(\varepsilon(v)=E_{0}\left(R_{0}\right)+\hbar \omega(v+1 / 2), \quad v=0,1,2 \ldots\)(7.32)

Las energías de excitación de los estados vibracionales moleculares son típicamente mayores que las de los estados rotacionales por un factor de aproximadamente\(\left(m_{N} / m_{e}\right)^{1 / 2}\) y más pequeñas que las energías de excitación electrónicas en un factor de aproximadamente\(\left(m_{e} / m_{N}\right)^{1 / 2}\). Como comentamos anteriormente,\(E_{0}(R_{0})\) serán del mismo orden de magnitud que las energías atómicas, es decir, del orden de\(\hbar^{2} / m_{e} a_{0}^{2}\), donde\(a_{0}\) está el radio de Bohr. Así, por motivos dimensionales,\(\left.\partial_{R}^{2} E_{0}\right|_{R_{0}}\) será de orden\(\hbar^{2} / m_{e} a_{0}^{4}\), y\(\hbar \omega \sim \hbar^{2} / \sqrt{m_{e} m_{N}} a_{0}^{2}\). Por lo tanto, la energía vibratoria es menor que la electrónica por un factor de orden\(\sqrt{m_{e} / m_{N}}\). Esto pone espectros vibracionales en la región de longitud de onda alrededor\(10μ\mathrm{m}\), que está en el infrarrojo.

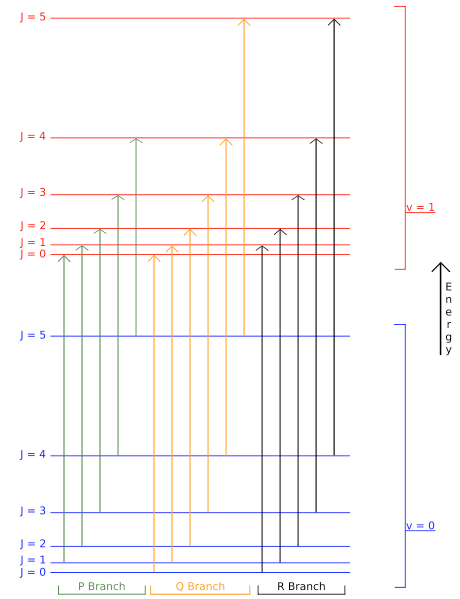
Figura 7.6: Generalmente las transiciones vibracionales ocurren junto con transiciones rotacionales. En consecuencia, es posible observar transiciones tanto rotacionales como vibracionales en el espectro vibracional. La figura superior muestra un diagrama de nivel de energía que demuestra algunas de las transiciones involucradas en el espectro vibratorio-rotacional IR de una molécula lineal: rama P (donde\(ΔJ=−1\)), rama Q (no siempre permitida\(ΔJ=0\)) y rama R (\(ΔJ=+1\)).
http://en.Wikipedia.org/wiki/File:Vibrationrotationenergy.svg

Figura 7.7: El espectro de vibración-rotación de HCl. La rama izquierda del espectro representa la rama P y la derecha la R. La rama Q no está permitida. La división de las líneas está asociada con los dos isótopos\(^{35}Cl\) y\(^{37}Cl\).

Ahora podemos comprobar explícitamente que la aproximación Born-Oppenheimer es válida para los estados vibracionales nucleares, de la siguiente manera. El impulso vibratorio nuclear cuadrático medio es de orden\(m_{N} \hbar \omega \sim \sqrt{m_{N} / m_{e}}\left(\hbar / a_{0}\right)^{2}\), lo que significa que\(\nabla_{N}^{2} \phi_{k} \sim \sqrt{m_{N} / m_{e}} \phi_{k} / a_{0}^{2}\), donde\(ϕ_{k}\) está la parte nuclear de la función de onda. Por otro lado\(\nabla_{N}^{2} \psi \sim \psi / a_{0}^{2}\), donde\(ψ\) está la parte electrónica. Así\(\phi \nabla_{N}^{2} \psi\) es menor que\(\psi \nabla_{N}^{2} \phi\) por un factor de\(\sqrt{m_{e} / m_{N}}\), y es legítimo descuidar al primero.

Para las transiciones vibracionales tenemos la regla de selección\(Δv=±1\). Esto implica solo una sola energía en el espectro

\(\Delta \varepsilon=\left(\varepsilon_{v+1}-\varepsilon_{v}\right)=\hbar \omega\)(7.33)

correspondiente a la frecuencia clásica de oscilación.

Efectos anarmónicos

En la práctica, la expansión de Taylor alrededor\(R=R_{0}\) tiene términos no despreciables de más de segundo orden y la aproximación del oscilador armónico no es muy confiable: hay anharmonicidad. El aplanamiento de la curva de energía potencial molecular en separaciones mayores tiene el efecto de acercar los niveles de energía. Así, las transiciones a vv mayores tienen energías más bajas que las dadas anteriormente. Además, dado que las verdaderas funciones de onda de estado estacionario no son precisamente funciones propias del oscilador armónico, nuestra regla de selección no es exactamente válida, y las transiciones con\(|v|>1\) se vuelven posibles. Una buena aproximación del potencial que incluye efectos anarmónicos es el llamado potencial Morse que tiene la forma:

\(E_{0}(R)=D_{e}\left(1-e^{-a\left(R-R_{e}\right)}\right)^{2}\)(7.34)

donde\(D_{e}\) está la energía de disociación, el límite al que converge el potencial en\(R→∞\). El mínimo del potencial está en el valor\(R_{e}\) de equilibrio de la distancia entre los átomos. La definición en (7.31) rinde:

\(\omega=a \sqrt{2 D_{e} / \mu}\)(7.35)

Figura 7.8: El potencial Morse (azul) y el potencial del oscilador armónico (verde). A diferencia de los niveles de energía del potencial del oscilador armónico, que están espaciados uniformemente por | (ω\), el espaciamiento del nivel del potencial Morse disminuye a medida que la energía se acerca a la energía de disociación.
http://en.Wikipedia.org/wiki/File:Morse-potential.png

La ecuación de valor propio del Hamiltoniano vibracional correspondiente\(\frac{P^{2}}{2 \mu}+D_{e}\left(1-e^{-a(R-R e)}\right)^{2}\) en una dimensión se puede resolver en forma cerrada produciendo los valores propios exactos:

\(\varepsilon(v)=E_{0}\left(R_{0}\right)+\hbar \omega\left(v+\frac{1}{2}\right)-\frac{\hbar^{2} \omega^{2}}{4 D_{e}}\left(v+\frac{1}{2}\right)^{2}, \quad v=0,1,2 \ldots\)(7.36)

Esto proporciona la separación de energía

\(\Delta \varepsilon(v)=\hbar \omega\left(1-\frac{\hbar \omega}{2 D_{e}}(v+1)\right)\)(7.37)

lo que significa que las frecuencias de transición están disminuyendo, con números cuánticos vibracionales crecientes. En contraste con el caso armónico el número de estados unidos es finito\([s]+1\), donde\(s=\frac{\sqrt{2 \mu D_{e}}}{\hbar \alpha}-1 / 2\), y\([s]\) denota la parte entera de s.

Los modos vibracionales para moléculas poliatómicas pueden ser bastante complicados. Si hay átomos de N, en general hay modos\(3N−6\) normales (\(3N\)coordenadas menos 3 para definir la posición general del centro de masa, y menos 3 para definir la orientación general de la molécula) o\(3N−5\) en el caso de una molécula diatómica. Así, en el caso simple de la\(\mathrm{CO}_{2}\) molécula lineal, existen cuatro modos, dos con los átomos permaneciendo colineales (uno con los dos átomos de O moviéndose en antifase con el C estacionario, y uno con los átomos de O moviéndose en fase en dirección opuesta al átomo de C) y dos flexión ortogonal degenerada modos. La clasificación más detallada de los posibles modos vibracionales de las moléculas poliatómicas se basa fuertemente en sus propiedades de simetría y necesita el método matemático llamado teoría de grupos.

Figura 7.9: Los niveles electrónicos combinados de vibración y rotación de una molécula. Vemos que la mayor diferencia energética es entre los estados electrónicos. El espectro electrónico consiste en un sistema de bandas vibracionales, mientras que cada banda vibracional incluye muchas líneas rotacionales.