2.2: Álgebra lineal

Introducción

Hemos visto que en la mecánica cuántica, el estado de un electrón en algún potencial viene dado por una función de onda\(\psi(\vec x,t)\), y las variables físicas son representadas por operadores en esta función de onda, como el impulso en la dirección x\(p_x =-i\hbar\partial/\partial x\). La ecuación de onda de Schrödinger es una ecuación lineal, lo que significa que si\(\psi_1\) y\(\psi_2\) son soluciones, entonces así es\(c_1\psi_1+c_2\psi_2\), donde\(c_1, c_2\) están los números complejos arbitrarios.

Esta linealidad de los conjuntos de posibles soluciones es cierta generalmente en la mecánica cuántica, al igual que la representación de las variables físicas por parte de los operadores sobre las funciones de onda. La estructura matemática que esto describe, el conjunto lineal de estados posibles y conjuntos de operadores en esos estados, es de hecho un álgebra lineal de operadores que actúan sobre un espacio vectorial. A partir de ahora, este es el lenguaje que usaremos la mayor parte del tiempo. Para aclarar, daremos algunas definiciones.

¿Qué es un Espacio Vectorial?

El espacio vectorial prototípico es, por supuesto, el conjunto de vectores reales en el espacio tridimensional ordinario, estos vectores pueden ser representados por tríos de números reales que\((v_1,v_2,v_3)\) miden los componentes en las direcciones x, y y z respectivamente.

Las propiedades básicas de estos vectores son:

• cualquier vector multiplicado por un número es otro vector en el espacio,\(a(v_1,v_2,v_3)=(av_1,av_2,av_3)\);
• la suma de dos vectores es otro vector en el espacio, que se da simplemente sumando los componentes correspondientes:\((v_1+w_1,v_2+w_2,v_3+w_3)\).

Estas dos propiedades juntas se denominan “cierre”: sumar vectores y multiplicarlos por números no puede sacarte del espacio.

• Una propiedad adicional es que hay un vector nulo único\((0,0,0)\) y cada vector tiene una inversa aditiva\((-v_1,-v_2,-v_3)\) que sumada al vector original da el vector nulo.

Los matemáticos han generalizado la definición de un espacio vectorial: un espacio vectorial general tiene las propiedades que hemos enumerado anteriormente para vectores reales tridimensionales, pero las operaciones de suma y multiplicación por un número se generalizan a operaciones más abstractas entre entidades más generales. Sin embargo, los operadores están restringidos a ser conmutativos y asociativos.

Observe que la lista de propiedades necesarias para un espacio vectorial general no incluye que los vectores tengan una magnitud, eso sería un requisito adicional, dando lo que se llama un espacio vectorial normado. Más sobre eso más tarde.

Para pasar del espacio vectorial tridimensional familiar a los espacios vectoriales relevantes para la mecánica cuántica, primero los números reales (componentes del vector y posibles factores multiplicadores) deben generalizarse a números complejos, y segundo el vector de tres componentes va a un vector de n componentes. El consiguiente espacio complejo n-dimensional es suficiente para describir la mecánica cuántica del momento angular, un tema importante. Pero para describir la función de onda de una partícula en una caja se requiere un espacio dimensional infinito, una dimensión para cada componente de Fourier, y para describir la función de onda para una partícula en una línea infinita requiere el conjunto de todas las funciones diferenciables continuas normalizables en esa línea. Afortunadamente, todas estas generalizaciones son conjuntos finitos o infinitos de números complejos, por lo que los requisitos de espacio vectorial de conmutatividad y asociatividad de los matemáticos siempre se satisfacen trivialmente.

Usamos la notación de Dirac para los vectores,\(|1\rangle,|2\rangle\) y los llamamos “kets”, entonces, en su idioma, si\(|1\rangle,|2\rangle\) pertenecen al espacio, también lo hace\(c_1|1\rangle +c_2|2\rangle\) para constantes complejas arbitrarias\(c_1, c_2\). Dado que nuestros vectores están formados por números complejos, multiplicar cualquier vector por cero da el vector nulo, y la inversa aditiva se da invirtiendo los signos de todos los números en el vector.

Claramente, el conjunto de soluciones de la ecuación de Schrödinger para un electrón en un potencial satisface los requisitos para un espacio vectorial:\(\psi(\vec x,t)\) es solo un número complejo en cada punto del espacio, por lo que solo los números complejos están involucrados en la formación\(c_1\psi_1+c_2\psi_2\), y la conmutatividad, asociatividad, etc., siguen a la vez.

Dimensionalidad del espacio vectorial

Los vectores\( |1\rangle ,|2\rangle ,|3\rangle\) son linealmente independientes si\[ c_1|1\rangle +c_2|2\rangle +c_3|3\rangle =0 \tag{2.2.1}\]

implica\[ c_1=c_2=c_3=0 \tag{2.2.2}\]

Un espacio vectorial es n-dimensional si el número máximo de vectores linealmente independientes en el espacio es n.

A ese espacio se le suele llamar\(V^n(C)\), o\(V^n(R)\) si solo se utilizan números reales.

Ahora, los espacios vectoriales con dimensión finita n son claramente insuficientes para describir funciones de una variable continua x. Pero bien vale la pena revisarlas aquí: como hemos mencionado, están bien para describir el momento angular cuantificado, y sirven como una introducción natural a los espacios infinito-dimensionales necesarios para describir las funciones de onda espaciales.

Un conjunto de n vectores linealmente independientes en el espacio n -dimensional es una base; cualquier vector puede escribirse de una manera única como una suma sobre una base:\[ |V\rangle=\sum v_i|i\rangle \tag{2.2.3}\]

Se puede comprobar la singularidad tomando la diferencia entre dos sumas supuestamente distintas: será una relación lineal entre vectores independientes, una contradicción.

Dado que todos los vectores en el espacio pueden escribirse como sumas lineales sobre los elementos de la base, la suma de múltiplos de dos vectores cualesquiera tiene la forma:\[ a|V\rangle+b|W\rangle=\sum (av_i+bw_i)|i\rangle \tag{2.2.4}\]

Espacios interiores de productos

Los espacios vectoriales de relevancia en la mecánica cuántica también tienen una operación que asocia un número con un par de vectores, una generalización del producto puntual de dos vectores tridimensionales ordinarios,\[ \vec a, \vec b =\sum a_ib_i \tag{2.2.5}\]

Siguiendo Dirac, escribimos el producto interno de dos vectores ket\(|V\rangle,|W\rangle\) como\(\langle W|V\rangle\). Dirac se refiere a esta\(\langle \; | \; \rangle\) forma como un “soporte” compuesto por un “sujetador” y un “ket”. Esto significa que cada vector ket\(|V\rangle\) tiene un sujetador asociado\(\langle V|\). Para el caso de un vector n-dimensional real,\(|V\rangle,\langle V|\) son idénticos, pero requerimos para el caso más general que\[ \langle W|V\rangle=\langle V|W\rangle^*\tag{2.2.6}\]

donde\(*\) denota conjugado complejo. Esto implica que para un ket\((v_1,...,v_n)\) el sujetador será\((v_1^*,...,v_n^*)\). (En realidad, los sostenes suelen escribirse como filas, kets como columnas, de manera que el producto interno sigue las reglas estándar para la multiplicación matricial). Evidentemente para el vector complejo n-dimensional\(\langle V|V\rangle\) es real y positivo excepto para el vector nulo:

\[ \langle V|V\rangle=\sum_1^n |v_i|^2 \tag{2.2.7}\]

Para los espacios internos de producto más generales considerados posteriormente requerimos\(\langle V|V\rangle\) ser positivos, excepto para el vector nulo. (Estos requisitos sí restringen las clases de espacios vectoriales que estamos considerando, sin métrica de Lorentz, por ejemplo, pero todos están satisfechos por los espacios relevantes para la mecánica cuántica no relativista).

La norma de\(|V\rangle\) se define entonces por\[ |V|=\sqrt{\langle V|V\rangle} \tag{2.2.8}\]

Si\(|V\rangle\) es miembro de\(V^n(C)\), así es\(a|V\rangle\), para cualquier número complejo\(a\).

Requerimos que la operación interna del producto se conmute con multiplicación por un número, así

\[ \langle W|(a|V\rangle)=a\langle W|V\rangle \tag{2.2.9}\]

El complejo conjugado del lado derecho es\(a^*\langle V|W\rangle\). Para mayor consistencia, el sujetador correspondiente al ket\(a|V\rangle\) debe ser,\(\langle V|a^*\) en todo caso obvio a partir de la definición del sujetador en n dimensiones complejas dadas anteriormente.

De ello se deduce que si\[ |V\rangle=\sum v_i|i\rangle, \; |W\rangle=\sum w_i|i\rangle, \; then \; \langle V|W\rangle=\sum v_i^*w_j \langle i|j\rangle \tag{2.2.10}\]

Construyendo una base ortonormal: el proceso Gram-Schmidt

Para tener algo que se asemeje mejor al producto punto estándar de tres vectores ordinarios\(\langle i|j\rangle=\delta_{ij}\), necesitamos, es decir, necesitamos construir una base ortonormal en el espacio. Hay un procedimiento sencillo para hacer esto llamado proceso Gram-Schmidt. Comenzamos con un conjunto linealmente independiente de vectores base,\(|1\rangle, |2\rangle, |3\rangle\),....

Primero normalizamos dividiéndolo\(|1\rangle\) por su norma. Llame al vector normalizado\(|I\rangle\). Ahora\(|2\rangle\) no puede ser paralelo a\(|I\rangle\), porque la base original era de vectores linealmente independientes, pero\(|2\rangle\) en general tiene un componente distinto de cero paralelo a\(|I\rangle\), igual a\(|I\rangle\langle I|2\rangle\), ya que\(|I\rangle\) se normaliza. Por lo tanto, el vector\(|2\rangle-|I\rangle\langle I|2\rangle\) es perpendicular a\(|I\rangle\), como se verifica fácilmente. También es fácil calcular la norma de este vector, y dividirlo por él para obtener\(|II\rangle\), el segundo miembro de la base ortonormal. A continuación, tomamos\(|3\rangle\) y restamos sus componentes en las direcciones\(|I\rangle\) y\(|II\rangle\), normalizamos el resto, y así sucesivamente.

En un espacio n-dimensional, habiendo construido una base ortonormal con miembros\(|i\rangle\), cualquier vector\(|V\rangle\) puede escribirse como vector de columna,\[ |V\rangle= \sum v_i |i\rangle= \begin{pmatrix}v_1 \\ v_2 \\ . \\ . \\ v_n \end{pmatrix} \, , \; where \; |1\rangle= \begin{pmatrix}1 \\ 0 \\ . \\ . \\ 0 \end{pmatrix} \; and \: so \: on. \tag{2.2.11}\]

El sujetador correspondiente es\(\langle V|=\sum v_i^*\langle i|\), que escribimos como un vector de fila con los elementos complejos conjugados,\(\langle V|=(v_1^*,v_2^*,...v_n^*)\). Esta operación, pasando de columnas a filas y tomando el conjugado complejo, se llama tomar el adjunto, y también se puede aplicar a matrices, como veremos en breve.

La razón para representar el sujetador como una fila es que el producto interno de dos vectores se da entonces por la multiplicación de matriz estándar:\[ \langle V|W\rangle=(v_1^*,v_2^*,...,v_n^*) \begin{pmatrix}w_1\\ . \\ . \\ w_n \end{pmatrix} \tag{2.2.12}\]

(Por supuesto, esto sólo funciona con una base ortonormal).

La desigualdad de Schwartz

La desigualdad de Schwartz es la generalización a cualquier espacio interno del producto del resultado\(|\vec a ,\vec b|^2 \le |\vec a|^2|\vec b|^2\) (o\(\cos^2 \theta \le1\)) para vectores tridimensionales ordinarios. El signo de igualdad en ese resultado sólo se mantiene cuando los vectores son paralelos. Para generalizar a dimensiones superiores, uno podría simplemente notar que dos vectores están en un subespacio bidimensional, pero una manera iluminadora de entender la desigualdad es escribir el vector\(\vec a\) como una suma de dos componentes, uno paralelo\(\vec b\) y otro perpendicular a\(\vec b\). El componente paralelo a\(\vec b\) es justo\(\vec b(\vec a\cdot \vec b)/|\vec b|^2\), por lo que el componente perpendicular a\(\vec b\) es el vector\(\vec a_{\bot}=\vec a-\vec b(\vec a\cdot\vec b)/|\vec b|^2 \). Sustituyendo esta expresión en\(\vec a_{\bot}\cdot\vec a_{\bot} \ge0 \), sigue la desigualdad.

Este mismo punto se puede hacer en un espacio general de producto interno: si\(|V\rangle\),\(|W\rangle\) son dos vectores, entonces\[ |Z\rangle=|V\rangle-\frac{|W\rangle \langle W|V\rangle}{|W|^2} \tag{2.2.13}\]

es el componente de\(|V\rangle\) perpendicular a\(|W\rangle\), ya que se comprueba fácilmente tomando su producto interno con\(|W\rangle\).

Entonces\[ \langle Z|Z\rangle \ge0 \;\; gives\; immediately\;\; |\langle V|W\rangle|^2 \le |V|^2|W|^2 \tag{2.2.14}\]

Operadores Lineales

Un operador lineal A toma cualquier vector en un espacio vectorial lineal a un vector en ese espacio,\(A|V\rangle=|V'\rangle\) y satisface\[A(c_1|V_1\rangle+c_2|V_2\rangle)= c_1A|V_1\rangle+c_2A|V_2\rangle \tag{2.2.15}\]

con\(c_1\), constantes complejas\(c_2\) arbitrarias.

El operador de identidad\(I\) es (¡obviamente!) definido por:\[ I|V\rangle=|V\rangle \;\; for \; all \; |V\rangle \tag{2.2.16}\]

Para un espacio vectorial n-dimensional con una base ortonormal\(|1\rangle,...,|n\rangle\), dado que cualquier vector en el espacio se puede expresar como una suma\(|V\rangle=\sum v_i|i\rangle\), el operador lineal está completamente determinado por su acción sobre los vectores base, esto es todo lo que necesitamos saber. Es fácil encontrar una expresión para el operador de identidad en términos de sostenes y kets.

Tomando el producto interno de ambos lados de la ecuación\(|V\rangle=\sum v_i|i\rangle\) con el sujetador\(\langle i|\) da\(\langle i|V\rangle=v_i\), así\[ |V\rangle=\sum v_i|i\rangle=\sum |i\rangle\langle i|V\rangle \tag{2.2.17}\]

Dado que esto es cierto para cualquier vector en el espacio, se deduce que el operador de identidad es justo\[ I=\sum_1^n |i\rangle\langle i| \tag{2.2.18}\]

Este es un resultado importante: reaparecerá en muchos disfraces.

Para analizar la acción de un operador lineal general\(A\), solo necesitamos saber cómo actúa sobre cada vector base. Empezando con\(A|1\rangle\), esto debe ser alguna suma sobre los vectores base, y como son ortonormales, el componente en la\(|i\rangle\) dirección debe ser justo\(\langle i|A|1\rangle\).

Es decir,\[ A|1\rangle=\sum_1^n |i\rangle\langle i|A|1\rangle=\sum_1^n A_{i1}|i\rangle\, ,\; writing\; \langle i|A|1\rangle =A_{i1} \tag{2.2.19}\]

Entonces si el operador lineal A que actúa sobre\(|V\rangle=\sum v_i|i\rangle\) da\(|V'\rangle=\sum v_i'|i\rangle\), es decir\(A|V\rangle=|V'\rangle\), la linealidad nos dice que\[ \sum v_i'|i\rangle=|V'\rangle=A|V\rangle=\sum v_j A|j\rangle= \sum_{i,j} v_j |i\rangle\langle i|A|j\rangle=\sum_{i,j} v_j A_{ij}|i\rangle \tag{2.2.20}\]

donde en el cuarto paso acabamos de insertar el operador de identidad.

Dado que\(|i\rangle\) los s son todos ortogonales, el coeficiente de un particular\(|i\rangle\) en el lado izquierdo de la ecuación debe ser idéntico al coeficiente de la misma\(|i\rangle\) en el lado derecho. Es decir,\(v_i'=A_{ij}v_j\).

Por lo tanto, el operador\(A\) es simplemente equivalente a la multiplicación matricial:

\[\begin{pmatrix}v_1'\\ v_2'\\ .\\ .\\ v_n'\end{pmatrix}= \begin{pmatrix} \langle1|A|1\rangle &\langle1|A|2\rangle & .& .&\langle1|A|n\rangle\\ \langle2|A|1\rangle &\langle2|A|2\rangle & .& .& .\\ .& .& .& .& .\\ . & .& .& .& .\\ \langle n|A|1\rangle &\langle n|A|2\rangle & .& .&\langle n|A|n\rangle \end{pmatrix} \begin{pmatrix}v_1\\ v_2\\ .\\ .\\ v_n\end{pmatrix} \tag{2.2.21}\]

Evidentemente, entonces, aplicar dos operadores lineales uno tras otro equivale a la multiplicación matricial sucesiva y, por lo tanto, ya que las matrices en general no conmutan, ni los operadores lineales. (Por supuesto, si esperamos representar variables cuánticas como operadores lineales en un espacio vectorial, esto tiene que ser cierto: ¡el operador de impulso\(p=-i\hbar d/dx\) ciertamente no viaja con x!)

Operadores de Proyección

Es importante señalar que un operador lineal aplicado sucesivamente a los miembros de una base ortonormal podría dar un nuevo conjunto de vectores que ya no abarcan todo el espacio. Para dar un ejemplo, el operador lineal\(|1\rangle\langle 1|\) aplicado a cualquier vector en el espacio selecciona el componente del vector en la\(|1\rangle\) dirección. Se llama operador de proyección. El operador\((|1\rangle\langle 1|+|2\rangle\langle 2|)\) proyecta un vector en sus componentes en el subespacio abarcado por los vectores\(|1\rangle\) y\(|2\rangle\), y así sucesivamente-si extendemos la suma para que sea sobre toda la base, recuperamos el operador de identidad.

Ejercicio: demostrar que la representación matricial del operador de proyección\((|1\rangle\langle 1|+|2\rangle\langle 2|)\) tiene todos los elementos cero excepto los dos primeros elementos diagonales, que son iguales a uno.

No puede haber operador inverso a un operador de proyección no trivial, ya que se pierde la información sobre los componentes del vector perpendiculares al subespacio proyectado.

El operador adjunto y las matrices hermitianas

Como hemos comentado, si un ket\(|V\rangle\) en el espacio n-dimensional se escribe como un vector de columna con componentes\(n\) (complejos), el sujetador correspondiente es un vector de fila que tiene como elementos los conjugados complejos de los elementos ket. \(\langle W|V\rangle=\langle V|W\rangle^*\)luego se sigue automáticamente de las reglas de multiplicación matricial estándar, y al multiplicar\(|V\rangle\) por un número complejo\(a\) para obtener\(a|V\rangle\) (es decir, que cada elemento en la columna de números se multiplica por\(a\)) el sujetador correspondiente va a\(\langle V|a^*=a^*\langle V|\).

Pero supongamos que en vez de multiplicar un ket por un número, operamos sobre él con un operador lineal. ¿Qué genera la transformación paralela entre los sostenes? Es decir, si\(A|V\rangle=|V'\rangle\), ¿\(\langle V|\)a qué operador envía el sostén\(\langle V'|\)? Debe ser un operador lineal, porque\(A\) es lineal, es decir, si bajo\(A\)\(|V_1\rangle \to |V_1'\rangle\),\(|V_2\rangle \to |V_2'\rangle\) y\(|V_3\rangle=|V_1\rangle +|V_2\rangle\), entonces\(A\)\(|V_3\rangle\) se requiere bajo para llegar a\(|V_3'\rangle=|V_1'\rangle +|V_2'\rangle\). En consecuencia, bajo la transformación paralela del sujetador debemos tener\(\langle V_1|\to \langle V_1'|\),\(\langle V_2|\to \langle V_2'|\) y\(\langle V_3|\to \langle V_3'|\), —la transformación del sujetador es necesariamente también lineal. Recordando que el sujetador es un vector de fila de n elementos, la transformación lineal más general que lo envía a otro sujetador es una\(n\times n\) matriz que opera sobre el sujetador desde la derecha.

Este operador de sujetador se llama el adjunto de\(A\), escrito\(A^{\dagger}\). Es decir, el ket\(A|V\rangle\) tiene sujetador correspondiente\(\langle V|A^{\dagger}\). En base ortonormal, utilizando la notación\(\langle Ai|\) para denotar el sostén\(\langle i|A^{\dagger}\) correspondiente al ket\(A|i\rangle=|Ai\rangle\), digamos,\[ (A^{\dagger})_{ij}=\langle i|A^{\dagger}|j\rangle=\langle Ai|j\rangle=\langle j|Ai\rangle^*=A_{ji}^* \tag{2.2..22}\]

Entonces el operador adjunto es el conjugado complejo de transposición.

Importante: para un producto de dos operadores (¡demuéstralo!) ,\[ (AB)^{\dagger}=B^{\dagger}A^{\dagger} \tag{2.2..23}\]

Un operador igual a su colindante\(A=A^{\dagger}\) se llama Hermitiano. Como veremos en la próxima conferencia, los operadores hermitianos son de importancia central en la mecánica cuántica. Un operador igual a menos su adjunto,\(A=-A^{\dagger}\), es anti hermitiano (a veces denominado sesgo hermitiano). Estos dos tipos de operadores son esencialmente generalizaciones de número real e imaginario: cualquier operador puede expresarse como una suma de un operador hermitiano y un operador anti hermitiano,\[ A=\frac{1}{2}(A+A^{\dagger})+\frac{1}{2}(A-A^{\dagger}) \tag{2.2.24}\]

La definición de adjunto se extiende naturalmente a vectores y números: la unión de un ket es el sujetador correspondiente, la unión de un número es su complejo conjugado. Esto es útil a tener en cuenta a la hora de tomar el conjunto de un operador que puede estar parcialmente construido de vectores y números, tales como operadores de tipo proyección. La unión de un producto de matrices, vectores y números es el producto de las uniones en orden inverso. (Por supuesto, para los números el orden no importa.)

Operadores Unitarios

Un operador es unitario si\(U^{\dagger }U=1\). Esto implica primero que\(U\) operar sobre cualquier vector da un vector que tenga la misma norma, ya que la nueva norma\(\langle V|U^{\dagger }U|V\rangle=\langle V|V\rangle\). Además, se conservan los productos internos,\(\langle W|U^{\dagger }U|V\rangle=\langle W|V\rangle\). Por lo tanto, bajo una transformación unitaria la base ortonormal original en el espacio debe ir a otra base ortonormal.

Por el contrario, cualquier transformación que tome una base ortonormal en otra es una transformación unitaria. Para ver esto, supongamos que una transformación lineal\(A\) envía los miembros de la base ortonormal\((|1\rangle_1,|2\rangle_1,...,|n\rangle_1)\) al conjunto ortonormal diferente\((|1\rangle_2,|2\rangle_2,...,|n\rangle_2)\)\(A|1\rangle_1=|1\rangle_2\), así, etc. entonces el vector\(|V\rangle= \sum v_i |i\rangle_1\) irá a\(|V'\rangle=A|V\rangle=\sum v_i |i\rangle_2\), teniendo la misma norma,\(\langle V'|V'\rangle= \langle V|V\rangle=\sum |v_i|^2\). Un elemento matricial\(\langle W'|V'\rangle= \langle W|V\rangle=\sum w_i^*v_i\), pero también\(\langle W'|V'\rangle=\langle W|A^{\dagger}A|V\rangle\). Es decir,\(\langle W|V\rangle= \langle W|A^{\dagger}A|V\rangle\) para kets arbitrarios\(|V\rangle, \: |W\rangle\). Esto sólo es posible si\(A^{\dagger}A=1\), así\(A\) es unitario.

Una operación unitaria equivale a una rotación (posiblemente combinada con una reflexión) en el espacio. Evidentemente\(U^{\dagger}U=1\), ya que, lo contiguo\(U^{\dagger}\) gira la base hacia atrás, es la operación inversa, y así\(UU^{\dagger}=1\) también, es decir,\(U\) y\(U^{\dagger}\) conmutar.

Determinantes

Revisamos en esta sección el determinante de una matriz, una función estrechamente relacionada con las propiedades del operador de la matriz.

Empecemos con\(2\times2\) matrices:\[ A=\begin{pmatrix} a_{11} &a_{12} \\ a_{21} &a_{22} \end{pmatrix} \tag{2.2.25}\]

El determinante de esta matriz se define por:\[ \det A=|A|=a_{11}a_{22}-a_{12}a_{21} \tag{2.2.26}\]

Escribiendo las dos filas de la matriz como vectores:\[ \vec a_1^R=(a_{11},a_{12}) \\ \vec a_2^R=(a_{21},a_{22}) \tag{2.2.27}\]

(\(R\)denota fila),\(\det A=\vec a_1^R \times \vec a_2^R\) es solo el área (con signo apropiado) del paralelogramo que tiene los dos vectores de fila como lados adyacentes:

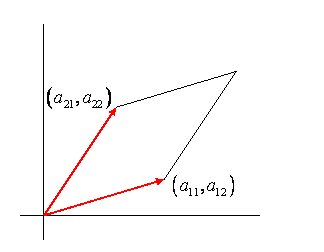
Esto es cero si los dos vectores son paralelos (linealmente dependientes) y no se cambia agregando ningún múltiplo de\(\vec a_2^R\) to\(\vec a_2^R\) (porque el nuevo paralelogramo tiene la misma base y la misma altura que el original; verifique esto dibujando).

Pasemos al caso más interesante de\(3\times3\) las matrices:\[ A=\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix} \tag{2.2.28}\]

El determinante de\(A\) se define como\[ \det A=\varepsilon_{ijk}a_{1i}a_{2j}a_{3k} \tag{2.2.29}\]

donde\(\varepsilon_{ijk}=0\) si dos cualesquiera son iguales, +1 if\(ijk = 123, \; 231 \; or\; 312\) (es decir, una permutación par de 123) y —1 si\(ijk\) es una permutación impar de 123. Los sufijos repetidos, por supuesto, implican aquí una suma.

Escribiendo esto explícitamente,\[ \det A= a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{11}a_{32}a_{23}-a_{21}a_{12}a_{33}-a_{31}a_{22}a_{13} \tag{2.2.30}\]

Al igual que en dos dimensiones, vale la pena mirar esta expresión en términos de vectores que representan las filas de la matriz\[ \vec a_1^R=(a_{11},a_{12},a_{13}) \\ \vec a_2^R=(a_{21},a_{22},a_{23}) \\ \vec a_3^R=(a_{31},a_{32},a_{33}) \tag{2.2.31}\]

por lo\[ A= \begin{pmatrix} \vec a_1^R\\ \vec a_2^R\\ \vec a_3^R \end{pmatrix} \: , \; and \; we \; see \; that \; \det A=(\vec a_1^R \times \vec a_2^R)\cdot \vec a_3^R \tag{2.2.32}\]

Este es el volumen del paralelepípedo formado por los tres vectores siendo lados adyacentes (reuniéndose en una esquina, el origen).

Este volumen paralelepípedo, por supuesto, será cero si los tres vectores se encuentran en un plano, y no se cambia si se agrega un múltiplo de uno de los vectores a otro de los vectores. Es decir, el determinante de una matriz no se cambia si se agrega un múltiplo de una fila a otra fila. Esto se debe a que el determinante es lineal en los elementos de una sola fila,\[ \det \begin{pmatrix} \vec a_1^R+\lambda\vec a_2^R \\ \vec a_2^R \\ \vec a_3^R \end{pmatrix}=\det \begin{pmatrix} \vec a_1^R\\ \vec a_2^R \\ \vec a_3^R \end{pmatrix} +\lambda\det \begin{pmatrix} \vec a_2^R\\ \vec a_2^R\\ \vec a_2^R \end{pmatrix} \tag{2.2.33}\]

y el último término es cero porque dos filas son idénticas, por lo que el producto de triple vector desaparece.

Una forma más general de afirmar esto, aplicable a determinantes mayores, es que para un determinante con dos filas idénticas, la simetría de las dos filas, junto con la antisimetría de\(\varepsilon_{ijk}\), asegura que los términos en la suma todos cancelen en pares.

Dado que el determinante no se altera agregando algún múltiplo de una fila a otra, si las filas son linealmente dependientes, una fila podría hacerse idéntica a cero agregando los múltiplos correctos de las otras filas. Dado que cada término en la expresión para el determinante tiene un elemento de cada fila, el determinante sería entonces idénticamente cero. Para el caso tridimensional, la dependencia lineal de las filas significa que los vectores correspondientes se encuentran en un plano, y el paralelepípedo es plano.

El argumento algebraico generaliza fácilmente a\(n\times n\) determinantes: son idénticamente cero si las filas son linealmente dependientes.

La generalización de\(3\times3\) a\(n\times n\) determinantes es que\(\det A=\varepsilon_{ijk}a_{1i}a_{2j}a_{3k}\) se convierte en:

\[ \det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}...a_{np} \tag{2.2.34}\]

donde\(ijk...p\) se suma sobre todas las permutaciones de\(132...n\), y el\(\varepsilon\) símbolo es cero si dos de sus sufijos son iguales, +1 para una permutación par y - 1 para una permutación impar. (Nota: cualquier permutación puede escribirse como producto de swaps de vecinos. Tal representación en general no es única, pero para una permutación dada, todas esas representaciones tendrán un número impar de elementos o un número par.)

Un teorema importante es que para un producto de dos matrices\(A\),\(B\) el determinante del producto es el producto de los determinantes,\(\det AB=\det A\times \det B\). Esto se puede verificar por fuerza bruta para\(2\times2\) matrices, y una prueba en el caso general se puede encontrar en cualquier libro sobre física matemática (por ejemplo, Byron y Fuller).

También se puede probar que si las filas son linealmente independientes, el determinante no puede ser cero.

(Aquí hay una prueba: tomar una\(n\times n\) matriz con los vectores de\(n\) fila linealmente independientes. Consideremos ahora los componentes de esos vectores en el subespacio\(n – 1\) dimensional perpendiculares a\((1, 0, ... ,0)\). Estos\(n\) vectores, cada uno con solo\(n – 1\) componentes, deben ser linealmente dependientes, ya que hay más de ellos que la dimensión del espacio. Entonces podemos tomar alguna combinación de las filas debajo de la primera fila y restarla de la primera fila para dejar la primera fila\((a, 0, 0, ... ,0)\), y a no puede ser cero ya que tenemos una matriz con filas\(n\) linealmente independientes. Entonces podemos restar múltiplos de esta primera fila de las otras filas para obtener un determinante que tenga ceros en la primera columna debajo de la primera fila. Ahora mira el\(n – 1\) por\(n – 1\) determinante para ser multiplicado por\(a\).

Sus filas deben ser linealmente independientes ya que las de la matriz original lo fueron. Ahora proceda por inducción.)

Para volver a tres dimensiones, queda claro a partir de la forma de\[ \det A= a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{11}a_{32}a_{23}-a_{21}a_{12}a_{33}-a_{31}a_{22}a_{13} \tag{2.2.30}\]

que igualmente podríamos haber tomado las columnas\(A\) como tres vectores,\(A=(\vec a_1^C, \vec a_2^C, \vec a_3^C) \) en una notación obvia,\(\det A=(\vec a_1^C \times \vec a_2^C)\cdot \vec a_3^C\), y la dependencia lineal entre las columnas también asegurará la fuga del determinante, así que, de hecho, la dependencia lineal de las columnas asegura lineal dependencia de las filas.

Esto, también, generaliza a\(n\times n\): en la definición de determinante\(\det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}...a_{np}\), el sufijo de fila es fijo y el sufijo de columna repasa todas las permutaciones permisibles, con el signo apropiado, pero los mismos términos se generarían teniendo los sufijos de columna mantenidos en orden numérico y permitiendo que el sufijo de fila se someta a las permutaciones.

Un Alado: Vectores Recíprocos De

Quizás valga la pena mencionar cómo se puede entender la inversa de un operador\(3\times 3\) matricial en términos de vectores. Para un conjunto de vectores linealmente independientes\((\vec a_1, \vec a_2, \vec a_3)\), se\((\vec b_1, \vec b_2, \vec b_3)\) puede definir un conjunto recíproco mediante\[ \vec b_1 =\frac{\vec a_2\times \vec a_3}{\vec a_1\times \vec a_2 \cdot \vec a_3} \tag{2.2.35}\]

y las definiciones cíclicas obvias para los otros dos vectores recíprocos. Vemos de inmediato que\[\vec a_i\cdot \vec b_j =\delta_{ij} \tag{2.2.36}\]

de lo que se deduce que la matriz inversa a\[ A=\begin{pmatrix} \vec a_1^R\\ \vec a_2^R \\ \vec a_3^R \end{pmatrix} \; is \; B=\begin{pmatrix}\vec b_1^C& \vec b_2^C& \vec b_3^C\end{pmatrix} \tag{2.2.37}\]

(Estos vectores recíprocos son importantes en la cristalografía de rayos x, por ejemplo. Si una red cristalina tiene ciertos átomos en posiciones\(n_1\vec a_1 +n_2\vec a_2+n_3\vec a_3\), donde\(n_1, n_2, n_3\) están los números enteros, los vectores recíprocos son el conjunto de normales a posibles planos de los átomos, y estos planos de átomos son los elementos importantes en la dispersión difractiva de rayos x.)

Eigenkets y Eigenvalues

Si un operador\(A\) que opera en un ket\(|V\rangle\) da un múltiplo del mismo ket,\[ A|V\rangle =\lambda|V\rangle \tag{2.2.38}\]

entonces\(|V\rangle\) se dice que es un eigenket (o, con la misma frecuencia, eigenvector, o eigenstate!) de\(A\) con valor propio\(\lambda\).

Los valores propios y propios son de importancia central en la mecánica cuántica: las variables dinámicas son operadores, una medición física de una variable dinámica produce un valor propio del operador y obliga al sistema a un eigenket.

En esta sección, mostraremos cómo encontrar los valores propios y los propios correspondientes para un operador\(A\). Usaremos la notación\(A|a_i\rangle =a_i|a_i\rangle\) para el conjunto de eigenkets\(|a_i\rangle\) con valores propios correspondientes\(a_i\). (Obviamente, en la ecuación de autovalor aquí el sufijo no\(i\) se suma.)

El primer paso para resolver\(A|V\rangle =\lambda|V\rangle\) es encontrar los valores propios permitidos\(a_i\).

Escribiendo la ecuación en forma de matriz:\[ \begin{pmatrix} A_{11}-\lambda & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-\lambda &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-\lambda \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ .\\ .\\ v_n \end{pmatrix} =0 \tag{2.2.39}\]

¡Esta ecuación en realidad nos está diciendo que las columnas de la matriz\(A-\lambda I\) son linealmente dependientes! Para ver esto, escribe la matriz como un vector de fila cada elemento del cual es una de sus columnas, y la ecuación se convierte en\[ (\vec M_1^C,\vec M_2^C,...,\vec M_n^C) \begin{pmatrix} v_1\\ .\\ .\\ .\\ v_n \end{pmatrix}=0 \tag{2.2.40}\]

que es decir\[ v_1\vec M_1^C+v_2\vec M_2^C+...+v_n\vec M_n^C=0 \tag{2.2.41}\]

las columnas de la matriz son de hecho un conjunto linealmente dependiente.

Sabemos que significa que el determinante de la matriz\(A-\lambda I\) es cero,\[ \begin{vmatrix} A_{11}-\lambda & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-\lambda &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-\lambda \end{vmatrix}=0 \tag{2.2.42}\]

Evaluar el determinante usando\(\det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}....a_{np}\) da un polinomio de\(n^{th}\) orden en\(\lambda\) algunas veces llamado polinomio característico. Cualquier polinomio puede escribirse en términos de sus raíces:\[ C(\lambda-a_1)(\lambda-a_2)....(\lambda-a_n)=0 \tag{2.2.43}\]

donde los\(a_i\)'s, las raíces del polinomio, y\(C\) es una constante global, que a partir de la inspección del determinante podemos ver que es\((-1)^n\). (Es el coeficiente de\(\lambda^n\).) Las raíces polinomiales (que aún no conocemos) son de hecho los valores propios. Por ejemplo, poner\(\lambda=a_1\) en la matriz\(\det (A-a_1I)=0\), lo que significa que\((A-a_1I)|V\rangle=0\) tiene una solución no trivial\(|V\rangle\), y este es nuestro autovector\(|a_1\rangle\).

Observe que el término diagonal en el determinante\((A_{11}-\lambda)(A_{22}-\lambda)....(A_{nn}-\lambda)\) genera los dos órdenes principales en el polinomio\((-1)^n(\lambda^{n}-(A_{11}+...+A_{nn})\lambda^{n-1})\), (y algunos términos de orden inferior también). Equiparando el coeficiente de\(\lambda^{n-1}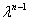\) aquí con el de\((-1)^n(\lambda-a_1)(\lambda-a_2)....(\lambda-a_n)\),\[ \sum_{i=1}^n a_i=\sum_{i=1}^n A_{ii}= Tr A \tag{2.2.44}\]

Poniendo\(\lambda=0\) tanto las representaciones determinantales como las polinomiales (es decir, equiparando los términos\(\lambda\) -independientes),\[ \prod_{i=1}^n a_i=\det A \tag{2.2.45}\]

Entonces podemos encontrar tanto la suma como el producto de los valores propios directamente del determinante, y para una\(2\times 2\) matriz esto es suficiente para resolver el problema.

Para cualquier cosa más grande, el método es resolver la ecuación polinómica\(\det (A-\lambda I)=0\) para encontrar el conjunto de valores propios, luego usarlos para calcular los vectores propios correspondientes. Esto se hace uno a la vez.

Etiquetando el primer valor propio encontrado como\(a_1\), la ecuación correspondiente para los componentes\(v_i\) v _i del autovector\(|a_1\rangle\) es\[ \begin{pmatrix} A_{11}-a_1 & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-a_1 &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-a_1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ .\\ .\\ v_n \end{pmatrix} =0 \tag{2.2.46}\]

Esto parece\(n\) ecuaciones para los\(n\) números\(v_i\), pero no lo es: recuerde que las filas son linealmente dependientes, así que solo hay ecuaciones\(n–1\) independientes. Sin embargo, eso es suficiente para determinar

las relaciones de los componentes del vector\(v_1,...,v_n\), luego finalmente se normaliza el vector propio. El proceso se repite entonces para cada eignevalue. (Se necesita un cuidado extra si el polinomio tiene raíces coincidentes; discutiremos ese caso más adelante).

Valores propios y estados propios de matrices hermitianas

Para una matriz hermitiana, es fácil establecer que los valores propios son siempre reales. (Nota: Un postulado básico de la Mecánica Cuántica, discutido en la siguiente conferencia, es que los observables físicos están representados por operadores hermitianos.) Tomando (en esta sección)\(A\) como hermitiano,\(A=A^{\dagger}\), y etiquetando los eigenkets por el valor propio, es decir,\[ A|a_1\rangle=a_1|a_1\rangle \tag{2.2.47}\]

el producto interior con el sujetador\(\langle a_1|\) da\(\langle a_1|A|a_1\rangle=a_1\langle a_1|a_1\rangle\). Pero el producto interno de la ecuación colindante (recordando\(A=A^{\dagger}\))\[ \langle a_1|A=a_1^*\langle a_1| \tag{2.2.48}\]

con\(|a_1\rangle\) da\(\langle a_1|A|a_1\rangle=a_1^*\langle a_1|a_1\rangle\), entonces\(a_1=a_1^*\), y todos los valores propios deben ser reales.

Ciertamente no tienen que ser todos diferentes —por ejemplo, la matriz unitaria\(I\) es hermitiana, y todos sus valores propios son, por supuesto, 1. Pero primero consideremos el caso donde todos son diferentes.

Es fácil demostrar que los eigenkets que pertenecen a diferentes valores propios son ortogonales.

Si\[ \begin{matrix} A|a_1\rangle=a_1|a_1\rangle \\ A|a_2\rangle=a_2|a_2\rangle \end{matrix} \tag{2.2.49}\]

tomar el adjunto de la primera ecuación y luego el producto interno con\(|a_2\rangle\), y compararlo con el producto interno de la segunda ecuación con\(\langle a_1|\):\[ \langle a_1|A|a_2\rangle=a_1\langle a_1|a_2\rangle=a_2\langle a_1|a_2\rangle \tag{2.2.50}\]

así\(\langle a_1|a_2\rangle=0\) que a menos que los valores propios sean iguales. (Si son iguales, se les denomina valores propios degenerados).

Primero consideremos el caso no degenerado:\(A\) tiene todos los valores propios distintos. Los eigenkets de\(A\), apropiadamente normalizados, forman una base ortonormal en el espacio.

Escribir\[ |a_1\rangle=\begin{pmatrix} v_{11}\\ v_{21}\\ \vdots\\ v_{n1}\end{pmatrix},\; and\, consider\, the\, matrix\; V=\begin{pmatrix} v_{11}&v_{12}&\dots&v_{1n} \\ v_{21}&v_{22}&\dots&v_{2n}\\ \vdots&\vdots&\ddots&\vdots \\ v_{n1}&v_{n2}&\dots&v_{nn} \end{pmatrix}=\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix} \tag{2.2.51}\]

Ahora\[ AV=A\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix}=\begin{pmatrix}a_1|a_1\rangle & a_2|a_2\rangle & \dots & a_n|a_n\rangle \end{pmatrix} \tag{2.2.52}\]

por lo\[ V^{\dagger}AV=\begin{pmatrix} \langle a_1|\\ \langle a_2|\\ \vdots\\ \langle a_n|\end{pmatrix}\begin{pmatrix}a_1|a_1\rangle & a_2|a_2\rangle & \dots & a_n|a_n\rangle \end{pmatrix}=\begin{pmatrix} a_1&0&\dots&0 \\ 0&a_2&\dots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\dots&a_n \end{pmatrix} \tag{2.2.53}\]

Obsérvese también que, obviamente,\(V\) es unitario:\[ V^{\dagger}V=\begin{pmatrix} \langle a_1|\\ \langle a_2|\\ \vdots\\ \langle a_n|\end{pmatrix}\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix}=\begin{pmatrix} 1&0&\dots&0 \\ 0&1&\dots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\dots&1\end{pmatrix} \tag{2.2.54}\]

Hemos establecido, entonces, que para una matriz hermitiana con valores propios distintos (caso no degenerado), la matriz unitaria\(V\) que tiene columnas idénticas a los eigenkets normalizados de\(A\) diagonaliza\(A\), es decir,\(V^{\dagger}AV\) es diagonal. Además, sus elementos (diagonales) son iguales a los valores propios correspondientes de\(A\).

Otra forma de decir esto es que la matriz unitaria\(V\) es la transformación de la base ortonormal original en este espacio a la base formada por los propios mercados normalizados de\(A\).

Prueba de que los vectores propios de una matriz hermitiana abarcan el espacio

Pasaremos ahora al caso general: ¿y si algunos de los valores propios de\(A\) son los mismos? En este caso, cualquier combinación lineal de ellos también es un vector propio con el mismo valor propio. Suponiendo que formen una base en el subespacio, el procedimiento de Gram Schmidt puede ser utilizado para hacerlo ortonormal, y así parte de una base ortonormal de todo el espacio.

Sin embargo, en realidad no hemos establecido que los vectores propios sí forman una base en un subespacio degenerado. ¿Podría ser que (para tomar el caso más simple) los dos vectores propios para el valor propio único resultan ser paralelos? Este es en realidad el caso de algunas\(2\times2\) matrices—por ejemplo,\(\begin{pmatrix}1&1\\0&1\end{pmatrix}\), necesitamos demostrar que no es cierto para las matrices hermitianas, y tampoco lo son las declaraciones análogas para los subespacios degenerados de dimensiones superiores.

Se da una clara presentación en Byron y Fuller, sección 4.7. Lo seguimos aquí. El procedimiento es por inducción del\(2\times2\) caso. La matriz\(2\times2\) hermitiana general tiene la forma\[ \begin{pmatrix}a&b\\b^*&c\end{pmatrix} \tag{2.2.55}\]

donde\(a\),\(c\) son reales. Es fácil comprobar que si los valores propios son degenerados, esta matriz se convierte en un múltiplo real de la identidad, y así trivialmente tiene dos autovectores ortonormales. Como ya sabemos que si los valores propios de\(2\times2\) una matriz hermitiana son distintos se puede diagonalizar por la transformación unitaria formada a partir de sus vectores propios ortonormales, hemos establecido que cualquier matriz\(2\times2\) hermitiana puede ser así diagonalizada.

Para llevar a cabo el proceso de inducción, ahora asumimos que cualquier matriz\((n-1)\times(n-1)\) hermitiana puede ser diagonalizada por una transformación unitaria. Tenemos que demostrar que esto significa que también es cierto para\(n\times n\) una matriz hermitiana\(A\). (Recordemos que una transformación unitaria toma una base ortonormal completa a otra. Si diagonaliza una matriz hermitiana, la nueva base es necesariamente el conjunto de vectores propios ortonormalizados. Por lo tanto, si la matriz puede ser diagonalizada, los vectores propios abarcan el espacio n-dimensional).

Elija un valor propio\(a_1\) de\(A\), con vector propio normalizado\(|a_1\rangle=(v_{11},v_{21},....,v_{n1})^T\). (Ponemos\(T\) para transponer, para salvar la torpeza de llenar la página con algunos vectores de columna.) Construimos un operador unitario\(V\) haciendo de ésta la primera columna, luego rellenando con\(n-1\) otros vectores normalizados para construir, con\(|a_1\rangle\), una base ortonormal n-dimensional.

Ahora, ya que\(A|a_1\rangle=a_1|a_1\rangle\), la primera columna de la matriz solo\(AV\) será\(a_1|a_1\rangle\), y las filas de la matriz\(V^{\dagger}=V^{-1}\) serán\(\langle a_1|\) seguidas por vectores\(n-1\) normalizados ortogonales a la misma, por lo que la primera columna de la matriz\(V^{\dagger}AV\) será \(a_1\)seguido de ceros. Es fácil comprobar que\(V^{\dagger}AV\) es hermitiano, ya que\(A\) es, por lo que su primera fila también es cero más allá del primer término diagonal.

Esto establece que para\(n\times n\) una matriz hermitiana existe una transformación unitaria para ponerla en la forma:\[ V^{\dagger}AV=\begin{pmatrix} a_1 &0&.&.&0\\ 0& M_{22}&.&.&M_{2n} \\ 0&.&.&.&. \\ 0&.&.&.&. \\ 0 &M_{n2}&.&.& M_{nn} \end{pmatrix} \tag{2.2.56}\]

Pero ahora podemos realizar una segunda transformación unitaria en el\((n-1)\times(n-1)\) subespacio ortogonal a\(|a_1\rangle\) (esto por supuesto deja\(|a_1\rangle\) invariante), para completar la diagonalización completa, es decir, la existencia de la\((n-1)\times(n-1)\) diagonalización, más el argumento anterior, garantiza la existencia de la\(n\times n\) diagonalización: la inducción es completa.

Diagonalización de una Matriz Hermitiana

Como se discutió anteriormente, una matriz hermitiana es diagonal en la base ortonormal de su conjunto de vectores propios:\(|a_1\rangle,|a_2\rangle,...,|a_n\rangle\), ya que\[ \langle a_i|A|a_j\rangle=\langle a_i|a_j|a_j\rangle=a_j\langle a_i|a_j\rangle=a_j\delta_{ij} \tag{2.2.57}\]

Si se nos dan los elementos matriciales de\(A\) en alguna otra base ortonormal, para diagonalizarla necesitamos rotar desde la base ortonormal inicial a una compuesta por los propios mercados de\(A\).

Denotando la base ortonormal inicial en la moda estándar\[ |1\rangle=\begin{pmatrix} 1\\0\\0\\ \vdots\\0\end{pmatrix}, \; |2\rangle=\begin{pmatrix} 0\\1\\0\\ \vdots\\0\end{pmatrix}, \; |i\rangle=\begin{pmatrix} 0\\ \vdots\\ 1\\ \vdots\\0\end{pmatrix}... \; (1\, in\, i^{th}\, place\, down), \; |n\rangle=\begin{pmatrix} 0\\0\\0\\ \vdots\\1\end{pmatrix} \tag{2.2.58}\]

los elementos de la matriz son\(A_{ij}=\langle i|A|j\rangle\).

Una transformación de una base ortonormal a otra es una transformación unitaria, como se discutió anteriormente, por lo que la escribimos\[ |V\rangle \to |V'\rangle=U|V\rangle \tag{2.2.59}\]

Bajo esta transformación, el elemento matriz\[ \langle W|A|V\rangle \to \langle W'|A|V'\rangle=\langle W|U^{\dagger}AU|V\rangle \tag{2.2.60}\]

Así podemos encontrar la matriz de transformación apropiada\(U\) requiriendo que\(U^{\dagger}AU\) sea diagonal con respecto al conjunto original de vectores base. (Transformar al operador de esta manera, dejando solo el espacio vectorial, equivale a rotar el espacio vectorial y dejar solo al operador. Por supuesto, en un sistema con más de un operador, se tendría que aplicar la misma transformación a todos los operadores).

De hecho, tal como discutimos para el caso no degenerado (valores propios distintos), la matriz unitaria\(U\) que necesitamos está compuesta solo por los propios mercados normalizados del operador\(A\),\[ U=(|a_1\rangle,|a_2\rangle,...,|a_n\rangle) \tag{2.2.61}\]

Y se deduce como antes que\[ (U^{\dagger}AU)_{ij}=\langle a_i|a_j|a_j\rangle=\delta_{ij}a_j, \; a\, diagonal\, matrix. \tag{2.2.62}\]

(Los sufijos repetidos aquí, por supuesto, no se suman.)

Si algunos de los valores propios son los mismos, el procedimiento de Gram Schmidt puede ser necesario para generar un conjunto ortogonal, como se mencionó anteriormente.

Funciones de Matrices

El mismo operador unitario\(U\) que diagonaliza una matriz\(A\) hermitiana también diagonalizará\(A^2\), porque\[ U^{-1}A^2U=U^{-1}AAU=U^{-1}AUU^{-1}AU \tag{2.2.63}\]

por lo\[ U^{\dagger}A^2U=\begin{pmatrix} a_1^2&0&0&.&0 \\ 0&a_2^2&0&.&0\\ 0&0&a_3^2&.&0 \\ .&.&.&.&. \\ 0&.&.&.&a_n^2\end{pmatrix} \tag{2.2.64}\]

Evidentemente, este mismo proceso funciona para cualquier potencia de\(A\), y formalmente para cualquier función de\(A\) expresable como una serie de potencias, pero por supuesto las propiedades de convergencia deben ser consideradas, y esto se vuelve más complicado al pasar de matrices finitas a operadores en espacios infinitos.

Matrices Hermitianas de Desplazamiento

De lo anterior, el conjunto de potencias de una matriz hermitiana todos conmutan entre sí, y tienen un conjunto común de vectores propios (pero no los mismos valores propios, obviamente). De hecho, no es difícil demostrar que dos matrices hermitianas cualesquiera que se desplazan entre sí tienen el mismo conjunto de vectores propios (después de posibles reordenamientos de Gram Schmidt en subespacios degenerados).

Si dos matrices\(n\times n\) hermitianas\(A\),\(B\) conmutan, es decir\(AB=BA\),, y\(A\) tiene un conjunto no degenerado de vectores propios\(A|a_i\rangle=a_i|a_i\rangle\)\(AB|a_i\rangle=BA|a_i\rangle=Ba_i|a_i\rangle=a_iB|a_i\rangle\), entonces, es decir,\(B|a_i\rangle\) es un vector propio de\(A\) con autovalor\(a_i\). Dado que no\(A\) es degenerado,\(B|a_i\rangle\) debe ser algún múltiplo de\(|a_i\rangle\), y concluimos que\(A\),\(B\) tienen el mismo conjunto de vectores propios.

Ahora supongamos que\(A\) es degenerado, y considera que el\(m\times m\) subespacio\(S_{a_i}\) abarcado por los vectores propios\(|a_i,1\rangle,\; |a_i,2\rangle,...\) de\(A\) tener valor propio\(a_i\). Aplicando el argumento del párrafo anterior, también\(B|a_i,1\rangle,\; B|a_i,2\rangle,...\) debe estar en este subespacio. Por lo tanto, si transformamos\(B\) con la misma transformación unitaria que diagonalizó\(A\), no\(B\) será en general diagonal en el subespacio\(S_{a_i}\), sino que será lo que se denomina diagonal de bloque, en que si\(B\) opera sobre algún vector en\(S_{a_i}\) él da un vector en\(S_{a_i}\).

\(B\)se pueden escribir como dos bloques diagonales: uno\(m\times m\), uno\((n-m)\times (n-m)\), con ceros fuera de estos bloques diagonales, por ejemplo, para\(m=2,\; n=5\):\[ \begin{pmatrix} b_{11}&b_{12}&0&0&0 \\ b_{21}&b_{22}&0&0&0 \\ 0&0&b_{33}&b_{34}&b_{35} \\ 0&0&b_{43}&b_{44}&b_{45} \\ 0&0&b_{53}&b_{54}&b_{55} \end{pmatrix} \tag{2.2.65}\]

Y, de hecho, si solo hay un valor propio degenerado ese segundo bloque solo tendrá términos distintos de cero en la diagonal:\[ \begin{pmatrix} b_{11}&b_{12}&0&0&0 \\ b_{21}&b_{22}&0&0&0 \\ 0&0&b_3&0&0 \\ 0&0&0&b_4&0 \\ 0&0&0&0&b_5 \end{pmatrix} \tag{2.2.65}\]

\(B\)por lo tanto opera en dos subespacios, uno m-dimensional, uno (n - m) -dimensional, independientemente —un vector enteramente en un subespacio permanece allí.

Esto significa que podemos completar la diagonalización de\(B\) con un operador unitario que solo opera en el\(m\times m\) bloque\(S_{a_i}\). Tal operador también afectará a los vectores propios de\(A\), pero eso no importa, porque todos los vectores en este subespacio son vectores propios de\(A\) con el mismo valor propio, por lo que en lo que a esto respecta, podemos elegir cualquier base ortonormal que nos guste —los vectores base seguirán\(A\) ser vectores propios.

Esto establece que cualquiera de dos matrices hermitianas de desplazamiento pueden ser diagonalizadas al mismo tiempo. Obviamente, esto nunca puede ser cierto de las matrices que no se desplazan, ya que todas las matrices diagonales conmutan.

Diagonalización de una Matriz Unitaria

Cualquier matriz unitaria puede ser diagonalizada por una transformación unitaria. Para ver esto, recordemos que cualquier matriz\(M\) puede escribirse como una suma de una matriz hermitiana y una matriz anti hermitiana,\[ M=\frac{M+M^{\dagger}}{2}+\frac{M-M^{\dagger}}{2}=A+iB \tag{2.2.66}\]

donde ambos\(A,\; B\) son hermitianos. Este es el análogo matricial de escribir un número complejo arbitrario como suma de partes reales e imaginarias.

Si se\(A,\; B\) conmutan, se pueden diagonalizar simultáneamente (ver la sección anterior), y por lo tanto se\(M\) pueden diagonalizar. Ahora bien, si una matriz unitaria se expresa en esta forma\(U=A+iB\) con\(A,\; B\) Hermitian, se desprende fácilmente de\(UU^{\dagger}=U^{\dagger}U=1\) ese\(A,\; B\) viaje, por lo que cualquier matriz unitaria\(U\) puede ser diagonalizada por una transformación unitaria. De manera más general, si una matriz\(M\) conmuta con su\(M^{\dagger}\) colindante, puede ser diagonalizada.

(Nota: no es posible diagonalizar a\(M\) menos que ambos\(A,\; B\) estén diagonalizados simultáneamente. Esto se deduce de\(U^{\dagger}AU,\; U^{\dagger}iBU\) ser hermitiano y antihermitiano para cualquier operador unitario\(U\), por lo que sus elementos fuera de diagonal no pueden cancelarse entre sí, todos deben ser cero si M ha sido diagonalizado por\(U\), en cuyo caso las dos matrices transformadas\(U^{\dagger}AU,\; U^{\dagger}iBU\) son diagonales, por lo tanto, conmutar, y también lo hacen las matrices originales\(A,\; B\).)

Vale la pena mirar un ejemplo específico, una simple rotación de una base ortonormal a otra en tres dimensiones. Obviamente, el eje a través del origen alrededor del cual se gira la base es un vector propio de la transformación. Está menos claro cuáles podrían ser los otros dos vectores propios, o, de manera equivalente, ¿cuáles son los vectores propios correspondientes a una rotación bidimensional de base en un plano? La manera de averiguarlo es anotar la matriz y diagonalizarla.

La matriz\[ U(\theta)=\begin{pmatrix} \cos \theta &\sin \theta\\ -\sin \theta &\cos \theta\end{pmatrix} \tag{2.2.67}\]

Obsérvese que el determinante es igual a la unidad. Los valores propios se dan resolviendo\[ \begin{vmatrix} \cos \theta -\lambda &\sin \theta\\ -\sin \theta &\cos \theta -\lambda\end{vmatrix}=0\; to\, give\; \lambda=e^{\pm i\theta} \tag{2.2.68}\]

Los vectores propios correspondientes satisfacen

\[ \begin{pmatrix} \cos \theta &\sin \theta\\ -\sin \theta &\cos \theta\end{pmatrix}\dbinom{u_1^{\pm}}{u_2^{\pm}}=e^{\pm i\theta}\dbinom{u_1^{\pm}}{u_2^{\pm}} \tag{2.2.69}\]

Los vectores propios, normalizados, son:\[ \dbinom{u_1^{\pm}}{u_2^{\pm}}=\frac{1}{\sqrt{2}}\dbinom{1}{\pm i} \tag{2.2.70}\]

Obsérvese que, a diferencia de una matriz hermitiana, los valores propios de una matriz unitaria no tienen que ser reales. De hecho, de\(U^{\dagger}U=1\), intercalado entre el sujetador y ket de un vector propio, vemos que cualquier valor propio de una matriz unitaria debe tener módulo unitario, es un número complejo en el círculo unitario. En retrospectiva, deberíamos habernos dado cuenta de que un valor propio de una rotación bidimensional tenía que ser\(e^{i\theta}\), el producto de dos rotaciones bidimensionales se le da estar sumando los ángulos de rotación, y una rotación a través de los\(\pi\) cambios de todos los signos, así lo tiene el valor propio\(-1\). Tenga en cuenta que el propio vector en sí es independiente del ángulo de rotación: todas las rotaciones se desplazan, por lo que deben tener vectores propios comunes. Los operadores de rotación sucesivos aplicados al vector propio más agregan sus ángulos, cuando se aplican al vector propio menos, se restan todos los ángulos.

Colaborador

• Michael Fowler (Beams Professor, Department of Physics, University of Virginia)