3.1: Ecuación de Schrödinger 1-D - Sistemas de ejemplo

Curvatura de Ondas

Ecuación de Schrödinger en la forma\[ \frac{d^2\psi(x)}{dx^2}=\frac{2m(V(x)-E)}{\hbar^2}\psi(x) \label{3.1.1}\]

se puede interpretar diciendo que el lado izquierdo, la tasa de cambio de pendiente, es la curvatura — por lo que la curvatura de la función es proporcional a\((V(x)-E)\psi(x)\). Esto significa que si\(E>V(x)\), para\(\psi(x)\) positivo\(\psi(x)\) está curvando negativamente, para\(\psi(x)\) negativo\(\psi(x)\) está curvando positivamente. En ambos casos, siempre\(\psi(x)\) está curvándose hacia el eje x —así, pues\(E>V(x)\),\(\psi(x)\) tiene una especie de estabilidad: su curvatura siempre la está trayendo de nuevo hacia el eje, y generando así oscilaciones. El ejemplo más simple es el de un potencial constante\(V(x)=V_0<E\), para lo cual la función de onda es

\[\psi(x)=A\sin(kx+\delta) \label{PIB1}\]

con\(\delta\) una constante y

\[k=\sqrt{(2m/\hbar^2)(E−V_0)}.\]

Por otro lado, para\(V(x)>E\), la curvatura siempre está alejada del eje. Esto significa que\(\psi(x)\) tiende a divergir hasta el infinito. Solo con exactamente las condiciones iniciales correctas la curvatura será la correcta para llevar la función de onda a cero como\(x\) va al infinito. (Esto es posible porque como\(\psi(x)\) tiende a cero, la curvatura tiende a cero, también).

Para un potencial constante\(V_0>E\), la función de onda es

\[\psi(x)=Ae^{\alpha x}+Be^{−\alpha x}\]

con

\[\alpha=\sqrt{(2m/\hbar^2)(V_0−E)}.\]

¡Por supuesto, esta función de onda divergirá en al menos una dirección! Sin embargo, como veremos más adelante, hay situaciones con potenciales espacialmente variables donde esta función de onda solo es relevante para positivo\(x\), y los coeficientes\(A\),\(B\) son funciones de la energía —para ciertas energías resulta que\(A=0\), y la función ondulatoria converge.

Pozo Cuadrado de Profundidad Infinita Unidimensional

En una conferencia anterior, consideramos con cierto detalle las funciones de onda y energías permitidas para una partícula atrapada en un pozo cuadrado infinitamente profundo, es decir, entre muros infinitamente altos a una distancia de\(L\) distancia. Para ese caso, el potencial entre las paredes es idéntico cero por lo que la función de onda tiene la forma (Ecuación\ ref {PIB1}). La función ondulada\(\psi(x)\) necesariamente va a cero justo en las paredes, ya que no puede tener una discontinuidad, y debe ser cero justo dentro de la pared. ¡Incluso una partícula cuántica no puede penetrar una pared infinita!

Una consecuencia inmediata es que el estado más bajo no puede tener cero energía, ya que\(k=0\) da una constante\(\psi(x)\). Más bien, el estado de energía más bajo debe tener la mínima cantidad de flexión de la función ondulada necesaria para que sea cero en ambas paredes pero distinto de cero en el medio — esto corresponde a medio periodo de un seno o coseno (dependiendo de la elección de origen), siendo estas funciones las soluciones de La ecuación de Schrödinger en la región de potencial cero entre las paredes. Las funciones de onda permitidas (estados propios) que se encuentran a medida que aumenta la energía tienen sucesivamente 0, 1, 2,... ceros (nodos) en el pozo.

Paridad de una función de onda

Observe que las funciones propias de onda permitidas del hamiltoniano para el pozo infinito son simétricas o antisimétricas alrededor del centro:

\[\psi(x)=\pm\psi(−x).\]

Llamamos al operador que refleja una función en el origen el operador de paridad\(P\), por lo que estos autoestados del hamiltoniano también son autoestados del operador de paridad, con valores propios\(\pm 1\). Esto se debe a que el hamiltoniano es en sí mismo simétrico:\(d^2/dx^2\) está incluso en\(x\)\(V(x)\), y así es\([H,P]=0\), así, y los dos operadores pueden diagonalizarse simultáneamente, es decir, se puede construir un conjunto común de autoestados.

Pozo Cuadrado de Profundidad Finita

Si el potencial en las paredes no es infinito, el operador de paridad\(P\) continuará viajando con el hamiltoniano\(H\) siempre y cuando el potencial sea simétrico,\(V(x)=V(−x)\).

Tomamos

\[ \begin{matrix} V(x)=V_0,& x<−L/2,\\ V(x)=0,& −L/2≤x≤L/2,\\ V(x)=V_0,& L/2<x.\end{matrix} \label{3.1.2}\]

Solo necesitamos buscar soluciones simétricas o antisimétricas sobre el origen. Esto es importante desde un punto de vista práctico, porque nos permite integrar numéricamente la ecuación de Schrödinger desde el origen en la dirección positiva:\(\psi(x)\) en la dirección negativa se fija por simetría (o antisimetría). Dado que es una ecuación de segundo orden, necesitamos dos condiciones de límite para ponernos en marcha, para estados simétricos, podemos tomar en x=0, para estados antisimétricos,\(\psi(x)=0\),\(\psi′(x)=1\) at\(x=0\). (Por supuesto, eventualmente tendremos que normalizarnos\(\psi(x)\) correctamente).

La estrategia numérica es elegir un valor para la energía\(E\), elegir una de las condiciones límite anteriores e integrar\(\psi(x)\) numéricamente a un gran valor positivo de\(x\). Para casi todos los valores de\(E\), la función de onda aumentará exponencialmente con\(x\). Para los valores particulares correspondientes a estados encuadernados, será exponencialmente decreciente.

Vale la pena construir una intuición para esto jugando con la hoja de cálculo que acompaña a esta conferencia: la hoja de cálculo hace la integración numérica para cualquier profundidad\(E\) y pozo, y tiene una macro para localizar el estado encuadernado más cercano.

Uniéndose a las ondulaciones dentro y fuera del pozo

El método numérico mencionado anteriormente funciona para cualquier potencial simétrico. Afortunadamente, para el pozo cuadrado, un método analítico/gráfico es muy efectivo, y proporciona más perspicacia.

Comencemos por considerar cómo se ve afectada la función de onda del estado de energía más baja al tener paredes finitas en lugar de infinitas. Dentro del pozo, donde\(V=0\), la solución a la ecuación de Schrödinger sigue siendo de forma coseno (para un estado simétrico). Sin embargo, la ecuación de Schrödinger ahora tiene una solución distinta de cero dentro de la pared\((x>L/2)\), donde\(V=V_0\):

\[−\frac{\hbar^2}{2m}\frac{d^ 2\psi(x)}{d x^2}+V_0\psi(x)=E\psi(x), \label{3.1.3}\]

tiene dos soluciones exponenciales, una creciente con\(x\), la otra decreciente,

\[ e^{\alpha x}\; and\; e^{−\alpha x} \label{3.1.4}\]

donde\(\alpha=\sqrt{2m(V_0−E)/\hbar^2}.\) Estamos suponiendo aquí que\(E<V_0\), así la partícula está ligada al pozo. Encontraremos que el estado energético más bajo está siempre ligado en un pozo cuadrado finito, por débil que sea el potencial.

Ahora, la ecuación de Schrödinger debe ser válida en todas partes, incluido el punto\(x=L/2\). Dado que el potencial es finito, la función de onda\(\psi(x)\) y su primera derivada deben ser continuas en\(x=L/2\).

Supongamos, entonces, que elegimos una energía particular\(E\). Entonces la función de onda dentro del pozo (tomando el caso simétrico) es proporcional a coskx, donde\(k=\sqrt{2mE/\hbar^2}\). La función de onda (¡y su derivada!) debe coincidir con una suma de términos exponenciales en\(x=L/2\), por lo que

\[ \begin{matrix} \cos(kL/2)=Ae^{\alpha L/2}+Be^{−\alpha L/2}\\ −k\sin(kL/2)=\alpha Ae^{\alpha L/2}−\alpha Be^{−\alpha L/2} \end{matrix} \label{3.1.5}\]

Resolviendo estas ecuaciones para los coeficientes\(A\),\(B\) de la manera habitual, encontramos que en general la solución coseno dentro del pozo entra suavemente en una combinación lineal de términos exponencialmente crecientes y decrecientes en la pared. Sin embargo, esto no puede representar en general un estado ligado en el pozo. La solución creciente aumenta sin límite a medida que\(x\) va al infinito, por lo que dado que el cuadrado de la función de onda es proporcional a la probabilidad de encontrar la partícula en cualquier punto, es infinitamente más probable que la partícula se encuentre en el infinito que en cualquier otro lugar. ¡Se escapó! Esto claramente no tiene sentido — estamos tratando de encontrar funciones de onda para partículas que permanecen en, o al menos cerca de, el pozo. Nos vemos obligados a concluir que la única función de onda exponencial que tiene sentido es aquella para la que\(A\) es exactamente cero, de manera que solo hay una onda decreciente en la pared.

Encontrar gráficamente las energías del estado unido

Si exigimos que la función de onda disminuya exponencialmente como\(x\) va al infinito, o, en otras palabras, requerimos que A sea cero,\(k\) debemos satisfacer la condición dada de estar dividiendo una de las ecuaciones límite anteriores por la otra:

\[ \tan(kL/2)=\alpha/k. \label{3.1.6}\]

Esta ecuación no se puede resolver analíticamente, pero es fácil de resolver gráficamente trazando los dos lados como funciones de\(k\) (recordar\(\alpha=\sqrt{2m(V_0−E)/\hbar^2}\), y\(k=\sqrt{2mE/\hbar^2}\)) y encontrar dónde se cruzan las curvas.

Desde\[ \alpha^2=\frac{2mV_0}{\hbar^2}−k^2 \;\; we\; find \;\; \frac{\alpha}{k}=\sqrt{\frac{2mV_0}{\hbar^2k^2}−1} \label{3.1.7}\]

tenga en cuenta que esto es real solo para\[ k<\frac{\sqrt{2mV_0}}{\hbar}. \label{3.1.8}\]

(Porque si esta desigualdad no se satisface, ¡la partícula tiene suficiente energía cinética para salir del pozo!)

Ahora se puede escribir la condición para un estado encuadernado

\[ \tan(kL/2)=\frac{\alpha}{k}=\sqrt{\frac{2mV_0}{\hbar^2k^2}−1} \label{3.1.9}\]

Limpiar la apariencia de la ecuación eligiendo variables\(x=\frac{kL}{2}\),\(a^2=\frac{mV_0L^2}{2\hbar^2}\), y trazando\(\tan x\) y\(\sqrt{(\frac{a}{x})^2−1}\) desde\(x=0\) el estado límite\(x=a\) permitido\(k\) -los valores corresponden a los puntos de intersección de las dos curvas. Las energías del estado unido son dadas entonces por\(E=\hbar^2k^2/2m\).

La variable\(a\) es una medida de la fuerza atractiva del pozo. Aquí están las dos curvas para un pozo poco profundo (\(a=1\)):

Es interesante señalar que por pequeña que\(a\) sea, la curva\(y=\sqrt{(\frac{a}{x})^2−1}\) va al infinito como\(x\) va a cero, así que siempre se cruzará\(y=\tan x\): siempre habrá un estado encuadernado.

Un pozo más profundo,\(a=20\), da varios estados ligados:

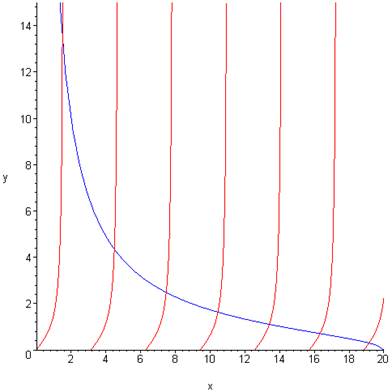
Para las energías inferiores al menos, los\(k\) valores permitidos están aproximadamente linealmente espaciados, a aproximadamente\(\pi/2\),\(3\pi/2\),\(5\pi/2\),... así que las energías del estado unido no están muy lejos del 1, 9, 25,... patrón del pozo cuadrado infinitamente profundo — recordando que solo estamos mirando el par soluciones de paridad (coseno)!

Ejercicio\(\PageIndex{1}\)

Usa la hoja de cálculo con D = 50, W = 4 y encuentra todas las energías de estado ligadas pares. ¿Qué tan bien encajan en este patrón? ¿Se puede dar cuenta de la desviación? Examine las funciones de onda para las diferentes energías propias: observe qué tan lejos penetra en la pared, y cuánto cambia la condición límite en la pared de la de una pared infinita. ¿Cuál de las energías del estado ligado es más afectada por esto, y cómo se ve afectada? ¿Eso lo esperarías de la solución gráfica?

Las soluciones de paridad impares, las ondas sinusoidales dentro del pozo, se pueden encontrar mediante un análisis exactamente similar. Una diferencia es que un pozo arbitrariamente débil no vinculará a un estado de paridad impar. El punto es que para que un potencial débil se vincula a un estado par, solo tiene que curvar ligeramente la función ondulada para pasar de una que decae exponencialmente a la izquierda a una que decae exponencialmente a la derecha. Estas curvas decaen muy lentamente para un potencial débil, y dan un estado unido en el que es más probable que la partícula se encuentre fuera del pozo. Por otro lado, en una extraña solución la función de onda dentro del pozo tiene que tener suficiente curvatura total para encajar dos ondulaciones en descomposición que tienen signo opuesto. Esto requiere mucha más flexión, y no se puede lograr con un potencial muy débil.

Ejercicio\(\PageIndex{2}\)

Revisa esta última afirmación, considerando qué fracción de una longitud de onda de la onda oscilante dentro del pozo es necesaria para hacer una conexión entre las ondulaciones en descomposición en las paredes a izquierda y derecha.

El potencial de la función Delta

Un caso limitante de un pozo cuadrado es un pozo profundo muy estrecho, que puede aproximarse mediante una función delta cuando el rango de variación de la función de onda es mucho mayor que el rango del potencial, por lo que la ecuación de Schrödinger se convierte en\[-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+\lambda\delta(x)\psi(x)=E\psi(x) \label{3.1.10}\]

con\(\lambda\) negativo para un potencial atractivo.

La infinidad de la\(\delta\) función -no puede ser equilibrada por el lado derecho finito, por lo que la función ondulada debe tener una discontinuidad en pendiente en el origen.

Para encontrar la energía del estado fundamental, tenga en cuenta primero que como potencial atractivo unidimensional habrá un estado límite: cualquier cambio en la pendiente es suficiente para conectar una función exponencialmente creciente que viene de\(−\infty\) a una decreciente que va a\(+\infty\), ya que las tasas de aumento y disminución puede ser arbitrariamente lento.

Lejos del origen, entonces, podemos tomar la ondafunción para ser\[ \psi(x)=Ae^{−\alpha|x|}, \label{3.1.11}\]

la energía del ser estatal\(E=−\hbar^2\alpha^2/2m\).

La discontinuidad en pendiente en el origen es solo\[ \frac{d\psi(x=+\varepsilon)}{dx}−\frac{d\psi(x=−\varepsilon)}{dx}=−2A\alpha.\label{3.1.12}\]

Para hacer coincidir esto con la singularidad\(\delta\) -función, integramos la ecuación de Schrödinger término por término de\(−\varepsilon\) a\(+\varepsilon\) en el límite de\(\varepsilon\) ir a cero:

\[ \int_{-\varepsilon}^{\varepsilon}-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}dx+\int_{-\varepsilon}^{\varepsilon}\lambda \delta(x)\psi(x)dx=\int_{-\varepsilon}^{\varepsilon}E\psi(x)dx. \label{3.1.13}\]

Obsérvese primero que el lado derecho, al tener un integrando finito, debe ir a cero en el límite de\(\varepsilon\) ir a cero.

El término\(\delta\) -función debe integrarse a\(\lambda\psi(0)=\lambda A\).

El primer término solo da la discontinuidad en pendiente,

\[ \int_{-\varepsilon}^{\varepsilon}-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}dx=-\frac{\hbar^2}{2m}\int_{-\varepsilon}^{\varepsilon}\frac{d}{dx}\left( \frac{d\psi}{dx}\right) dx=−\frac{\hbar^2}{2m}\left[ \frac{d\psi}{dx}\right]^{\varepsilon}_{−\varepsilon}=\frac{\hbar^2}{2m}2A\alpha. \label{3.1.14}\]

Por lo tanto, la ecuación de Schrödinger se satisface si\(\hbar^2\alpha/m+\lambda =0\) (recordar\(\lambda\) es negativo para un potencial atractivo).

La energía del estado atado es\[ E=−\frac{\hbar^2\alpha^2}{2m}=−\frac{m\lambda^2}{2\hbar^2}.\label{3.1.15}\]

Ejercicio\(\PageIndex{1}\)

Rederivar este resultado tomando el límite de un pozo profundo estrecho, tendiendo a una\(\delta\) función, con una función de onda coseno en su interior.

Un paso potencial

Nuestro análisis hasta ahora se ha limitado a soluciones de valor real de la ecuación de Schrödinger independiente del tiempo. Esto está bien para analizar estados ligados en un potencial, o ondas estacionarias en general, pero no se puede usar, por ejemplo, para representar un electrón que viaja por el espacio después de ser emitido por un cañón de electrones, como en un tubo de televisión anticuado. La razón es que una función de onda de valor real\(\psi(x)\), en una región energéticamente permitida, se compone de términos localmente similares\(\cos kx\) y\(\sin kx\), multiplicada en la función de onda completa por el factor de fase dependiente del tiempo\(e^{-iEt/\hbar}\), dando amplitudes iguales de ondas en movimiento derecho\(e^{i(px−Et)/\hbar}\) y olas en movimiento a la izquierda\(e^{−i(px+Et)/\hbar}\). Entonces, para que un electrón definitivamente se mueva hacia la derecha, incluso la parte independiente del tiempo de la función de onda debe ser necesariamente compleja.

Considere un electrón de energía que\(E\) se mueve en una dimensión a través de una región de potencial cero desde un gran negativo\(x\) y encontrarse con un potencial de escalón ascendente de altura\(V_0\) (\(V_0<E\)) en el origen\(x=0\). Por supuesto, estrictamente hablando, el electrón debería estar representado por un paquete de ondas, y por lo tanto no podría tener una energía definida con precisión\(E\), pero suponemos aquí que es un paquete de onda muy larga, muy cercano a una onda plana, así que tomamos que la función de onda es:\[ \psi(x,t)=Ae^{ikx}e^{-iEt/\hbar}\;\; for\;\; x< 0 \label{3.1.16}\]

(Un análisis más preciso, en el que se usa un paquete de ondas entrantes, se puede hacer resolviendo los componentes de onda plana individualmente. En el límite de un paquete de ondas largo en comparación con la longitud de onda de Broglie, el resultado es el mismo que el que se encuentra aquí.)

Visualizando el cuadro clásico de una partícula acercándose a una colina (suavizando un poco las esquinas) que definitivamente tiene suficiente energía para superar, tal vez esperaríamos que la ondulación continúe más allá\(x=0\) en la forma\[ \psi(x,t)=Be^{ik_1x}e^{-iEt/\hbar}\;\; for\;\; x>0,\label{3.1.17}\]

donde\(k_1\) corresponde a la velocidad más lenta que tendrá la partícula después de subir el cerro.

La ecuación de Schrödinger requiere que la función de onda no tenga discontinuidades ni torceduras (discontinuidades en pendiente) por lo que las funciones de\(x>0\) onda\(x<0\) y ondas deben coincidir suavemente en el origen. Para que tengan el mismo valor, vemos desde arriba eso\(A=B\). Para que tengan la misma pendiente debemos tener \(kA=k_1B\). Desafortunadamente, la única manera de satisfacer ambas ecuaciones con nuestras funciones de onda anteriores es tomar,\(k=k_1\) ¡lo que significa que no hay ningún potencial de paso en absoluto!

Ejemplo\(\PageIndex{1}\)

¿Qué tiene de malo el razonamiento anterior?

¿Solución?

La respuesta es que hemos sido desviados por la representación de las partículas como pequeñas bolas rodando a lo largo de un potencial, con suficiente energía para subir la colina, etc. La ecuación de Schrödinger es una ecuación de onda. Construir la intuición sobre las soluciones debe basarse en la experiencia con las olas. Deberíamos estar pensando en una onda de luz que va del aire al vidrio, por ejemplo. Si lo hacemos, nos damos cuenta de que en cualquier interfaz parte de la luz se refleja. Esto quiere decir que nuestra expresión para la ondafunción para\(x<0\) es incompleta, necesitamos agregar una onda reflejada, dando

\[ \begin{matrix}\psi(x,t)=Ae^{ikx}e^{-iEt/\hbar} +Ce^{-ikx}e^{-iEt/\hbar}& for& x<0,\\ \psi(x,t)=Be^{ik_1x}e^{-iEt/\hbar} & for& x>0. \end{matrix} \label{3.1.18}\]

Ahora coincidiendo con la función de onda y su derivada en el origen,\[ \begin{matrix} A+C=B\\ k(A−C)=k_1B.\end{matrix} \label{3.1.19}\]

La fracción de la onda que se refleja\[ R=\frac{C^2}{A^2}=\left( \frac{k−k_1}{k+k_1}\right)^2. \label{3.1.20}\]

Evidentemente, la fracción de la onda transmitida\[ T=1−R=\frac{4kk_1}{(k+k_1)^2} .\label{3.1.21}\]

Ejemplo\(\PageIndex{2}\)

¿No es el monto transmitido que acaba de dar\(B^2/A^2\)?

¿Solución?

La respuesta es no. La relación\(B^2/A^2\) da la probabilidad relativa de encontrar una partícula en alguna región pequeña en la corriente transmitida en relación con la de la corriente entrante, pero las partículas en la corriente transmitida se mueven más lentamente, por un factor\(k_1/k\). Eso significa que no basta con comparar las densidades de partículas en las corrientes transmitidas y entrantes. La cantidad físicamente significativa es la corriente de probabilidad que fluye más allá de un punto dado, y este es el producto de la densidad y la velocidad. Por lo tanto, el coeficiente de transmisión es\(B^2k_1/A^2k\).

Ejercicio\(\PageIndex{1}\)

Demostrar que incluso un paso hacia abajo da lugar a alguna reflexión.

Hacer un túnel a través de una barrera cuadrada

Si una onda plana que viene desde la izquierda encuentra un paso en el origen de la altura\(V_0>E\), la energía entrante, habrá reflexión total, pero con una onda exponencialmente en descomposición penetrando cierta distancia en el escalón. Esto, por cierto, es un fenómeno de onda general, no confinado a la mecánica cuántica. Si una onda de luz que viaja a través de un trozo de vidrio está totalmente internamente en la superficie, habrá un campo electromagnético exponencialmente en descomposición en el aire fuera de la superficie. Si se acerca otra pieza de vidrio con una superficie paralela (plana), algo de luz “atravesará” el espacio de aire hacia la segunda pieza de vidrio. Estamos considerando aquí el análogo cuántico de este comportamiento clásico.

Supongamos entonces que sustituimos el escalón por una barrera,\[ \begin{matrix} V=0& for& x<0,& call\; this\; region\; I\\ V=V_0& for& 0<x<L,& this\; is\; region\; II\\ V=0& for& L<x,& region\; III.\end{matrix}\label{3.1.22}\]

En esta situación, la función de onda seguirá decayendo exponencialmente en la barrera (asumiendo que la barrera es gruesa en comparación con la longitud de decaimiento exponencial), pero al llegar al extremo lejano en\(x=L\), se permite nuevamente una solución de onda plana, por lo que existe una probabilidad distinta de cero de encontrar la partícula más allá del barrera, moviéndose con su velocidad original. A este fenómeno se le llama tunelización, ya que en la imagen clásica (partícula) la partícula no tiene suficiente energía para sobreponerse a la parte superior de la barrera.

La forma de resolver el problema es resolver la ecuación de Schrödinger en las tres regiones, luego aplicar las condiciones de contorno. Ya que nos interesa la probabilidad de que una partícula atraviese la barrera, no necesitamos preocuparnos por normalizar la función de onda, así que por simplicidad tomamos una onda entrante de amplitud unitaria. En la región I, también habrá una onda reflejada, por lo que\[ \psi_I(x)=e^{ikx}+Be^{-ikx}. \label{3.1.23}\]

En la región II, en general habrá soluciones tanto exponencialmente decrecientes como exponencialmente crecientes, así que tomamos\[ \psi_{II}(x)=Ce^{\alpha x}+De^{-\alpha x}. \label{3.1.24}\]

Recordar\(\alpha=\sqrt{(2m/\hbar^2)(V_0-E)}\)

En la región III, solo existe la onda saliente, para facilitar las ecuaciones absorbimos un factor de fase en el coeficiente, y escribimos:\[ \psi_{III}(x)=Se^{ik(x-L)}.\label{3.1.25}\]

Ahora requerimos\(\psi(x)\) y\(\psi′(x)\) ser continuos en\(x=0\),\(L\). Los cálculos elementales conducen a\[ \begin{matrix}2ik=(ik+\alpha)C+(ik-\alpha)D\\ 2\alpha Ce^{\alpha L}=(ik+\alpha)S\\ 2\alpha De^{-\alpha L}=-(ik-\alpha)S. \end{matrix}\label{3.1.26}\]

Resolver estas ecuaciones da\[ S(k)=\frac{2k\alpha}{2k\alpha\cosh\alpha L+i(\alpha^2-k^2)\sinh\alpha L}. \label{3.1.27}\]

La probabilidad de tunelización es:\[ |S(k)|^2=\frac{4k^2\alpha^2}{(k^2+\alpha^2)^2\sinh^2\alpha L+4k^2\alpha^2}. \label{3.1.28}\]

Un límite importante es el de una barrera gruesa en comparación con la longitud de decaimiento,\(\alpha L\gg1\).

En este límite,\(\sinh^2\alpha L\approx \frac{1}{4}e^{2\alpha L}\), y usando\(\alpha=\sqrt{(2m/\hbar^2)(V_0-E)}\)\(E=\hbar^2k^2/2m\),, encontramos\[ |S(k)|^2\cong 16\left( \frac{E}{V_0}\right) \left( 1-\frac{E}{V_0}\right) e^{-2\alpha L}.\label{3.1.29}\]

En los problemas típicos de tunelización, el término dominante lejano es el\(e^{-2\alpha L}\), que puede diferir de la unidad en muchos órdenes de magnitud.

El problema tridimensional esféricamente simétrico

Los métodos desarrollados anteriormente para el sistema unidimensional son casi inmediatamente aplicables a un caso tridimensional muy importante: una partícula en un potencial esféricamente simétrico. Más adelante se dará un tratamiento más detallado —nos limitamos aquí a soluciones esféricamente simétricas de la ecuación de Schrödinger\(\psi(r,\theta,\phi)=\psi(r)\), un subespacio del espacio de todas las soluciones posibles que siempre incluye el estado fundamental.

El operador de energía cinética en los estados en este subespacio (donde\(d/d\theta\equiv 0\),\(d/d\phi\equiv 0\)) es\[ \frac{\vec{p}^2}{2m}=−\frac{\hbar^2\vec{\nabla}^2}{2m}=-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{d}{dr}). \label{3.1.30}\]

Es fácil verificar que si escribimos la función de onda\[ \psi(r)=\frac{u(r)}{r} \label{3.1.31}\]

la función\(u(r)\) obedece a la ecuación unidimensional\[ -\frac{\hbar^2}{2m}\frac{d^2u(r)}{dr^2}+V(r)u(r)=Eu(r) \label{3.1.32}\]

exactamente como una partícula en una dimensión, excepto que aquí sólo\(r\) es positiva, y\(u(r)\) debe ir a cero en el origen. (Si\(u(r)\) no va a cero,\(\psi(r)\) será en el mejor de los casos de orden\(1/r\) cerca del origen, y, volviendo momentáneamente a tres dimensiones,\(\vec{\nabla}^2\psi\sim \delta(\vec{r})\), por lo que la ecuación de Schrödinger no quedará satisfecha con ningún potencial realizable.)

Ejercicio: para un pozo cuadrado esférico,\(V=0\) si\(r<r_0\),\(V=V_0\) para\(r\ge r_0\), encontrar el valor mínimo\(V_0\) para el cual existe un estado unido para dada\(r_0\) y masa de partículas\(m\). Haga un boceto de la función de onda.

Decaimiento Alfa

Un buen ejemplo de tunelización, y que históricamente ayudó a establecer la validez de las ideas cuánticas a nivel nuclear, es\(\alpha\) -decaimiento. Ciertos núcleos inestables grandes se descomponen radioactivamente al emitir una\(\alpha\) partícula, un estado fuertemente unido de dos protones y dos neutrones. Se piensa que\(\alpha\) -las partículas pueden existir, al menos como resonancias de larga vida, dentro del núcleo. Para tal partícula, la fuerza nuclear fuerte pero de corto alcance crea un pozo esférico de profundidad finita que tiene una pared empinada más o menos coincidente con la superficie del núcleo. Sin embargo, también debemos incluir la repulsión electrostática entre la\(\alpha\) partícula y el resto del núcleo, un potencial\((1/4\pi\varepsilon_0)(Z-2)2e^2/r\) fuera del núcleo. Esto quiere decir que, como se ve desde el interior del núcleo, la pared en la superficie puede no ser un escalón sino una barrera, en el sentido que usamos la palabra anterior, un escalón hacia arriba seguido de un deslizamiento hacia abajo de la curva electrostática:

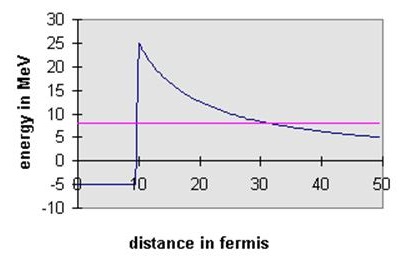
Por lo tanto, una\(\alpha\) partícula que rebota dentro del núcleo puede tener suficiente energía para atravesar el mundo exterior.

\(\alpha\)Las partículas se emiten con simetría esférica, por lo que la función de onda se puede escribir\(\psi(r)=u(r)/r\), como se discutió anteriormente, y la ecuación de Schrödinger es\[ -\frac{\hbar^2}{2m}\frac{d^2u(r)}{dr^2}+V(r)u(r)=Eu(r), \;\; r>0 \label{3.1.33}\]

Es evidente que cuanto más enérgica es la\(\alpha\) partícula, más delgada es la barrera a la que se enfrenta. Dado que la función de onda decae exponencialmente en la barrera, esto puede marcar una gran diferencia en las tasas de tunelización. No es difícil encontrar la energía con la que la\(\alpha\) -partícula golpea la pared nuclear, porque esta será la misma energía con la que escapa. Por lo tanto, si medimos la energía de una emitida\(\alpha\), ya que pensamos que conocemos bastante bien la forma de la barrera, deberíamos poder, al menos numéricamente, predecir la tasa de tunelización. Lo único que necesitamos saber es cuántas veces por segundo\(\alpha\) rebotan en la pared. El tamaño del núcleo es de orden\(10^{-14}\) metros (10 fermis), si asumimos un\(\alpha\) movimiento a, digamos,\(10^{7}\) metros por segundo, va a golpear en la pared\(10^{21}\) veces por segundo. Esto es un poco agitado, pero todos los\(\alpha\) núcleos radiactivos son más o menos del mismo tamaño, así que quizás sea seguro asumir que esto será aproximadamente lo mismo para todos ellos.

Este es un número enorme — ¡la probabilidad de transmisión es evidentemente muy pequeña! En otras palabras, la longitud de decaimiento de la función de onda dentro de la barrera es extremadamente corta (excepto por el último bit a medida que emerge al mundo exterior). Es tan corto, de hecho, que podemos obtener resultados en buena concordancia con el experimento dividiendo la barrera en una secuencia de barreras cuadradas y usando la\(\alpha L\gg 1\) fórmula anterior para cada una de ellas,\[ \psi(r+\Delta r)\approx \psi(r)e^{-\alpha(r)\delta r} \label{3.1.34}\]

(descuidando el\(1/r\) término que varía lentamente y completamente sin importancia) por lo que la atenuación total de la función de onda en esta aproximación es producto de términos como este,\[ \begin{matrix} \psi(exit)=\psi(nucl)\prod_i e^{-\alpha(r_i)\Delta r}\\ \approx \psi(nucl)e^{-\int \alpha(r)dr}\\ =\psi(nucl)e^{-\int \sqrt{(2m/\hbar^2)V(r)-E} dr} \end{matrix} \label{3.1.35}\]

Como conocemos la forma real de la barrera, esta integral se puede hacer con funciones elementales, y el resultado para la velocidad de transmisión es

\[ |S(k)|^2\approx Ae^{-B/\sqrt{E}}. \label{3.1.36}\]

Aquí no\(B=(\pi\sqrt{2m}/\hbar )(Z-2)2e^2\) hay un parámetro ajustable: y trazando\(\ln|S(k)|^2\) contra\(1/\sqrt{E}\) para Polonio ²¹² (que emite\(\alpha\) con energía 8.95MeV, y dura\(3\times 10^{-7}\) segundos) Torio ²³² (\(\alpha\)4.05MeV's,\(1.4\times10^{10}\) años), y varios intermedios núcleos de por vida da una gráfica en línea recta con la pendiente correcta dentro de unos pocos por ciento! Todos estos elementos pueden ser entendidos en términos de esencialmente la misma barrera que se realiza un túnel a través de las diferentes alturas correspondientes a la\(\alpha\) energía.

El tratamiento aquí es una versión ligeramente simplificada del método WKB, que se discutirá en detalle más adelante. Otros refinamientos hacen poca diferencia en el resultado final en este caso.

Fuente: muchos de los temas tratados en esta conferencia son elementales, y tratados en cualquier libro de texto cuántico. Para algunos de ellos he seguido (más o menos) el excelente libro de French y Taylor, An Introduction to Quantum Physics, Norton, 1978.

Colaborador

• Michael Fowler (Beams Professor, Department of Physics, University of Virginia)