13.13: Gato de Schrödinger

Desintegración radiactiva

Algunos elementos son inestables, decayendo a través de la interacción débil en otros elementos. Tales sustancias se llaman radiactivas. Por ejemplo, el Nitrógeno-13 se descompone en Carbono-13 más un electrón más un antineutrino.

Hay dos factores que determinan esa velocidad a la que se descompone una muestra de átomos radiactivos:

1. ¿Cuántos átomos hay? El doble de átomos tendrá una tasa de desintegración total que es el doble.
2. Cuál es la tendencia de un átomo particular a descomponerse.

La tendencia de un elemento a la descomposición se expresa por su vida media.

La vida media del Nitrógeno-13 es casi exactamente de 10 minutos. Lo que significa este número es que si tenemos una gran “olla” de Nitrógeno-13 y esperamos 10 minutos la mitad de los átomos de Nitrógeno-13 se habrán descompuesto y la mitad no se habrá descompuesto. Si esperamos otros 10 minutos la mitad de la muestra restante de átomos habrá decaído y la mitad no lo hará. Después de otros 10 minutos, la mitad de esa muestra restante habrá decaído.

El concepto de medio vivo es una especie de reminiscencia de una famosa paradoja de Xeno, quien argumentó que nunca podremos salir de una habitación. Si nos dirigimos hacia la puerta, eventualmente llegamos a la mitad de camino hacia ella. Si seguimos caminando habremos llegado a la mitad de la distancia restante hasta la puerta. Y entonces si seguimos caminando llegamos a la mitad de esa distancia restante. Así que seguimos llegando a mitad de camino hacia la puerta y nunca llegamos realmente.

Aquí hay algunas vidas medias:

Atom	Half-Vida
protones	> 10 ^32 años (es decir, consistente con ser estable
Carbono-14	5,730 años
Cobalto-60	1,925 días
Nitrógeno-13	10 minutos

Puedes acceder a una animación Flash de 500 átomos radiactivos del elemento ficticio Balonuim haciendo click aquí.

Para las sustancias radiactivas, un factor crucial en la discusión de la vida media es que estábamos discutiendo una gran colección de átomos. ¿Y si solo tenemos dos de esos átomos de Nitrógeno-13? Entonces si esperamos 10 minutos, una vida media, hay un 50% de posibilidades de que uno de los átomos se haya descompuesto. Entonces esto es algo similar a voltear dos monedas. Si una moneda en particular sale de cabeza es aproximadamente un 50% de probabilidad. Para voltear dos monedas podemos obtener ambas cabezas, una cabeza y una cola, o ambas colas. De igual manera para dos átomos radiactivos podríamos terminar con ambos en descomposición, uno en descomposición y el otro no, o ambos no en descomposición.

Imagínese que después de 10 minutos el átomo de la derecha se desintegró y el de la izquierda no se desintegró.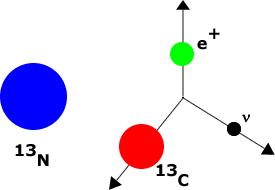

Hacemos una pregunta básica: ¿Cuál es la diferencia entre los dos átomos de Nitrógeno-13?

La respuesta a esto es trivialmente fácil: un átomo se desintegró y el otro no.

Una pregunta más interesante es: ¿Cuál era la diferencia entre los dos átomos de Nitrógeno-13 antes de esperar 10 minutos?

La respuesta a esta mejor pregunta es algo difícil. Según la Mecánica Cuántica no había diferencia entre los dos átomos: teníamos dos átomos completamente idénticos pero uno en descomposición y el otro no.

Einstein nunca aceptó la Mecánica Cuántica, y esta parte de la teoría es una de las razones. Resumió sus objeciones diciendo “Dios no juega a los dados con el universo”. Bohr respondió “¡Deja de decirle a Dios qué hacer!”

Puede que el Dios de Einstein no juegue a los dados, pero hay otras visiones de la divinidad. Por ejemplo, en el Bhagavad Gita Krishna dice:

“Yo soy el juego de los dados. Yo soy el egocéntrico en el corazón de todos los seres”.

Si, con Einstein, rechazamos la idea de que estados iniciales completamente idénticos puedan evolucionar a diferentes resultados, entonces concluimos que inicialmente debió haber alguna diferencia, alguna variable, que distinga a los dos átomos de Nitrógeno-13. A la fecha todos los intentos de descubrir qué es esa variable han fracasado; así diríamos que hay alguna variable oculta dentro de los átomos. En Mecánica Cuántica no existen tales variables.

La paradoja de los gatos

A principios de la década de 1930 Erwin Schrödinger publicó una forma de pensar sobre la circunstancia de la desintegración radiactiva que sigue siendo útil. Imaginamos un aparato que contiene solo un átomo de Nitrógeno-13 y un detector que responderá cuando el átomo decae. Conectado al detector hay un relé conectado a un martillo, y cuando el átomo se descompone, el relé libera el martillo que luego cae sobre un vial de vidrio que contiene gas venenoso. Tomamos todo el aparato y lo metemos en una caja. También colocamos un gato en la caja, cerramos la tapa y esperamos 10 minutos.

Entonces preguntamos: ¿El gato está vivo o muerto? La respuesta según la mecánica cuántica es que está 50% muerto y 50% vivo.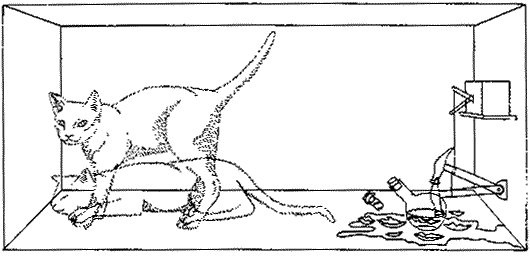

La Mecánica Cuántica describe el mundo en términos de una función de onda. DeWitt escribió sobre el gato que “al final de [una vida media] la función de onda total para el sistema tendrá una forma en la que el gato vivo y el gato muerto se mezclan en porciones iguales”. (Referencia: B.S. DeWitt y N. Graham, eds., La interpretación de muchos mundos de la mecánica cuántica (Princeton, 1973), pág. 156.)

Cuando abrimos la caja, “colapsamos la función de onda” o “colapsamos el estado” y tenemos ya sea un gato vivo o un gato muerto.

Por supuesto, esto es solo un experimento mental. Hasta donde yo sé, en realidad nadie ha hecho este experimento.

En cierto sentido el gato es un “arenque rojo” [¡lo siento!]. La paradoja no es más que una forma iluminadora de pensar que las consecuencias de la desintegración radiactiva son totalmente aleatorias.

Imagina que tenemos un amigo esperando afuera cuando abrimos la caja. Para nosotros la función de onda colapsa y tenemos, digamos, un gato vivo. Pero la función de onda de nuestro amigo no colapsa hasta que entra en la habitación. Esto lleva a un fuerte solipsismo, ya que nuestro amigo pueden decir que debemos nuestra existencia objetiva a su amable intervención en entrar a la habitación y colapsar nuestro estado.

Como dijo Heisenberg, entonces, “La función de onda representa en parte un hecho y en parte nuestro conocimiento de un hecho”.

Nuestro amigo no necesitaba haber entrado a la habitación para colapsar su función de onda: si tenemos un celular podemos llamarlo y decirle el resultado del experimento. Por supuesto, esto supone que no le mentimos y le decimos que el gato está muerto cuando está vivo.

Inexplicable pero aparentemente cierto es el hecho de que cuando un estado colapsa, colapsa en el mismo estado para todos. Si vemos un gato vivo todo el mundo ve un gato vivo (a menos que ellos o nosotros estemos alucinando).

Como comentó de Beauregard: “Finalmente, la necesidad de consistencia de todo el esquema me lleva a pensar en el mundo en el que vivimos como un mundo Leibnitziano, donde los gatos son bastante altos en la jerarquía de las mónadas”. Referencia: Fundamentos de la Física 6, 539 (1976).

Paradojas de la Mecánica Cuántica

Hay dos grandes paradojas de la Mecánica Cuántica, cada una ilustrando diferentes aspectos del misterio cuántico. El Gato de Schrödinger es uno de ellos, y el otro es el Doble Hendidura. Se puede acceder a las notas sobre la doble hendidura ya sea en html o pdf haciendo clic en los enlaces de la izquierda.

Cada paradoja muestra diferentes aspectos del “colapso del Estado”.

Doble Abertura

Muestra que el colapso del estado es real, irreversible, y provoca un cambio cualitativo en la evolución temporal posterior del sistema.

Gato de Schrödingers

Demuestra que nuestra conciencia y conocimiento están de alguna manera mezclados en este proceso.

Etiquetas recomendadas por la plantilla: article:topic