13.15: El modelo Bohr del Átomo

La estructura del átomo

A finales del siglo XIX, la mayoría de la gente había aceptado la propuesta de Dalton de 1808 de que la materia estaba hecha de átomos. Dalton “probó” su teoría con una serie de suposiciones, cada una de las cuales es fácticamente errónea o fue utilizada de una manera lógicamente inconsistente. Sin embargo, la oposición de críticos como Mach, que nunca creyó en los átomos, fue ignorada en gran medida. A lo largo del siglo XIX el atomismo se convirtió en una idea que llegó a dominar el pensamiento en una serie de campos, entre ellos la ciencia política, la sociología, la psicología, la biología y más.

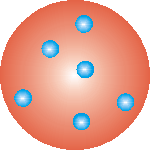Entonces, en 1897 J.J. Thomson descubrió el electrón. Determinó que estos electrones tenían una carga eléctrica negativa y en comparación con el átomo tenían muy poca masa. Así propuso que los átomos consistían en un gran cuerpo masivo cargado positivamente con una serie de pequeños electrones cargados negativamente dispersos por todo el mismo. La carga total de los electrones equilibró exactamente la carga positiva de la gran masa, por lo que la carga eléctrica total fue cero. A esto se le llamó el modelo de pudín de ciruela del átomo. El número de electrones determina el elemento químico particular. El hidrógeno, por ejemplo, tiene un electrón; el helio tiene dos; el carbono tiene seis, etc.

A principios del siglo XX Rutherford estaba experimentando con una de las sustancias radiactivas recién descubiertas, una que emitía partículas alfa. Sabía que estas partículas tenían una masa mucho mayor que el electrón y tenían una carga eléctrica neta positiva; ahora sabemos que estas partículas son idénticas al núcleo del átomo de helio. Estaba dirigiendo un haz de estas partículas alfa sobre una pieza muy delgada de lámina de oro. Si el modelo de pudín de ciruela de Thomson fuera correcto, los experimentos serían algo similares a disparar BB's de una pistola BB a una delgada losa de queso crema con cebolleta. Y de hecho los resultados de los experimentos de Rutherford solían seguir este modelo: casi todas las partículas alfa emergieron del otro lado ligeramente desviadas por su interacción con el oro. No obstante, de vez en cuando observó una partícula alfa que se dispersó de nuevo hacia la fuente radiactiva.

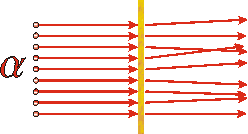
El diagrama anterior muestra cuál esperaríamos que fuera el resultado del experimento de Rutherford si el modelo de “pudín de ciruela” del átomo es correcto.

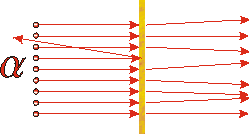
Lo anterior indica el resultado real. La mayoría de las partículas alfa solo están ligeramente desviadas, como se esperaba, pero ocasionalmente una es desviada de nuevo hacia la fuente.

Si estuvieras haciendo el experimento con los BB's y el queso crema y ocasionalmente tuvieras un BB esparcido hacia ti, probablemente concluirías que había algo bastante pequeño y muy masivo dentro de la losa. De igual manera, Rutherford concluyó que dentro de la lámina de oro debe haber algo bastante pequeño, muy masivo y cargado positivamente. Así el modelo de pudín de ciruela del átomo colapsó: la mayor parte de la masa y la carga positiva del átomo se concentró en un volumen muy pequeño. Este pequeño objeto masivo cargado positivamente se llama núcleo.

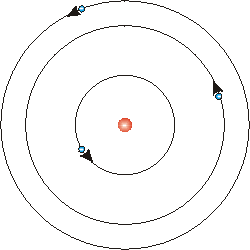Pronto, la gente propuso un modelo planetario del átomo. Los electrones estaban en órbitas alrededor del núcleo, sostenidos en sus órbitas por la fuerza eléctrica que atrae electrones cargados negativamente al núcleo cargado positivamente.

Sin embargo este modelo no tiene sentido. Sabemos por la teoría electromagnética clásica que cualquier cuerpo cargado que se encuentre en un estado de movimiento que no sea en reposo o en movimiento uniforme en línea recta emitirá energía como radiación electromagnética. Así los electrones es este modelo planetario va a estar irradiando energía. A medida que pierden energía entrarán en espiral hacia el núcleo y en cuestión de nanosegundos chocarán con él. Así este átomo no puede ser estable.

Modelo de Bohr

Neils Bohr conocía todos estos hechos, y a principios de siglo estaba colaborando con Rutherford. También conoció la existencia de espectros de líneas a partir de elementos químicos; aquí se puede encontrar un documento sobre este tema. Estaba luchando por darle sentido a todo esto. Como era común con Bohr cuando se enfrentaba a un rompecabezas, esta lucha estaba casi consumiendo todo.

Luego, en 1913 Bohr, por accidente, tropezó con la numerología de Balmer para el espectro de hidrógeno, y en un instante se le ocurrió un modelo viable del átomo. El modelo afirma que:

• El modelo planetario es correcto.
• Cuando un electrón está en una órbita “permitida” no irradia. Así, el modelo simplemente arroja la teoría electromagnética clásica. Nota técnica: una órbita permitida es aquella en la que la masa de electrones multiplicada por su velocidad por el radio de la órbita es igual a un entero positivo n veces la constante de Planck dividida por 2 pi. El entero n puede ser 1, 2, 3, 17, 108, etc. De hecho, hay un número infinito de órbitas permitidas correspondientes al número infinito de enteros positivos.
• Cuando un electrón absorbe energía de la radiación electromagnética incidente, “salta cuántico” a un estado permitido de mayor energía. Este estado de mayor energía corresponde a una órbita permitida con un valor mayor del entero n.
• Cuando un electrón se encuentra en un estado de energía superior, puede saltar cuántico a un estado de menor energía, uno con un valor menor de n, emitiendo toda su energía como un solo fotón de energía electromagnética.

Se ha preparado una animación Flash del modelo de Bohr que muestra la excitación y emisión de fotones del electrón en un átomo de hidrógeno. Requiere el reproductor Flash de la Versión 6 o superior; el reproductor está disponible de forma gratuita en http://www.macromedia.com/. El tamaño del archivo es 74k, y la animación aparecerá en una ventana separada. Para acceder a la animación haz clic aquí.

Nota técnica: las órbitas permitidas vienen dadas por la ecuación de la derecha, donde m es la masa del electrón, v es su velocidad, r es el radio de la órbita y h es la constante de Planck.

Como Bohr se dio cuenta plenamente, este modelo es en gran parte ad hoc, si no francamente feo. Sin embargo, sí “explica” los espectros lineales de los elementos.

Cuando Bohr publicó su modelo Otto Stern, que era el alumno de Einstein, y Max von Laue, que era alumno de Planck, hizo un voto serio: “¡Si esta tontería de Bohr al final resultara acertada, dejaremos la física!”

Dadas estas aseveraciones más las leyes clásicas estándar de atracción entre dos objetos cargados opuestamente, se puede calcular la energía de los electrones en sus órbitas en función del valor de n. Resulta depender de la masa y carga del electrón, la constante de Planck, algunas constantes de la teoría electromagnética, y también depende de 1/n ². La energía de las órbitas permitidas para el hidrógeno se muestra a la derecha; también hemos indicado el valor de n para tres de esos niveles de energía.

Nota técnica: el hecho de que las energías sean negativas sólo se debe a una convención común en cuanto a dónde elegimos el punto cero de la energía en un análisis no relativista.

Recordemos la fórmula de Balmer:

Aquí R es una constante igual a aproximadamente 10,970,000 y n es cualquier entero mayor que 2, como 3, 4, 5, 108, etc. cada valor diferente de n da la longitud de onda de una línea diferente en el espectro de hidrógeno. La constante R se suele llamar la constante de Rydberg.

Las longitudes de onda descritas por esta fórmula corresponden exactamente a la radiación emitida cuando un electrón en el modelo Bohr salta cuántico de una órbita de alta energía, descrita por algunos n mayores que 2, a una órbita cuyo valor de n es igual a 2. En el modelo también se predicen transiciones a otros estados “finales” como n igual a 1 o 3, 4, 5, etc. y se encuentra experimentalmente que las longitudes de onda en el espectro para estos existen. Además, la constante R resulta expresarse en términos de constantes físicas fundamentales. Así que hemos retrocedido un poco la numerología de la obra de Balmer.

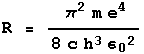Nota técnica: la constante de Rydberg viene dada por la ecuación de la derecha, donde m es la masa del electrón, e su carga, c es la velocidad de la luz, h es la constante de Planck, y la constante que relaciona las fuerzas ejercidas por la carga cuerpos unos sobre otros y las magnitudes de las cargas.

La órbita de menor energía permitida, la que tiene n igual a uno, es el estado fundamental del átomo. Un átomo de hidrógeno no excitado tendrá su electrón en este estado.

Explicando el modelo Bohr

En 1924 Louis de Broglie propuso que los electrones tienen una naturaleza de onda. Como parte de esa propuesta también describió la relación entre la longitud de onda del aspecto de onda y la masa y velocidad de su aspecto de partícula. La propuesta ha sido confirmada experimentalmente y es uno de los aspectos fundamentales de la Mecánica Cuántica.

Imagina un modelo planetario del átomo, pero ahora piensa en los electrones como ondas. ¿Qué estados de olas podrían estar permitidos?

Tal vez recuerdes que las olas que “encajan” en su espacio disponible, las ondas estacionarias, son las que están permitidas. Un documento en el que se discute esto está disponible aquí.

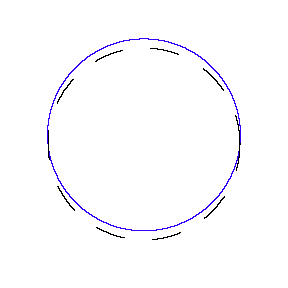
Mostramos algunas de las ondas estacionarias que pueden existir para una órbita circular.

Entonces, en general, la circunferencia es igual a n veces la longitud de onda, donde n es cualquier entero positivo. En las figuras anteriores el valor de n es 1, 2 y 3 respectivamente.

Puede ver una animación simple de cualquiera de las tres órbitas anteriores apuntándola y haciendo clic en el botón izquierdo. Si estás usando un navegador bastante moderno la animación aparecerá en una ventana separada; cierra esa ventana cuando quieras. Si estás usando un navegador más antiguo la animación aparecerá en esta ventana; usa el botón Atrás de tu navegador para volver aquí.

Resulta que estos estados de onda estacionaria para electrones corresponden exactamente a las órbitas de electrones “permitidas” en el modelo de Bohr. Entonces, la Mecánica Cuántica explica el modelo ad-hoc de Bohr del átomo.

Ahora llamamos al entero n el número cuántico principal. Tenga en cuenta que para el átomo de hidrógeno describe completamente el estado del electrón.

“Estamos rastreando la descripción de los fenómenos naturales hasta combinaciones de números puros que trascienden con creces los sueños más audaces de los pitagóricos”. — Bohr

Etiquetas recomendadas por la plantilla: article:topic