2: Los Postulados de la Mecánica Cuántica

Toda la estructura de la mecánica cuántica (incluyendo su extensión relativista) puede formularse en términos de estados y operaciones en el espacio Hilbert. Necesitamos reglas que mapeen las cantidades físicas como estados, observables y mediciones a la estructura matemática de espacios vectoriales, vectores y operadores. Hay varias formas en las que esto se puede hacer, y aquí resumimos estas reglas en términos de cinco postulados.

Hay una serie de aspectos importantes en este postulado. Primero, el hecho de que los estados sean rayos, más que vectores significa que una fase general\(e^{i \varphi}\) del estado no tiene consecuencias físicamente observables, y\(e^{i \varphi}|\psi\rangle\) representa el mismo estado que\(|\psi\rangle\). Segundo, el estado contiene toda la información sobre el sistema. En particular, no hay variables ocultas en esta formulación estándar de la mecánica cuántica. Por último, la dimensión de\(\mathscr{H}\) puede ser infinita, que es el caso, por ejemplo, cuando\(\mathscr{H}\) es el espacio de funciones integrables al cuadrado.

Como ejemplo de este postulado, consideremos un sistema cuántico de dos niveles (un qubit). Este sistema puede ser descrito por dos estados ortonormales\(|0\rangle\) y\(|1\rangle\). Debido a la linealidad del espacio Hilbert, la superposición\(\alpha|0\rangle+\beta|1\rangle\) vuelve a ser un estado del sistema si tiene la norma 1, o

\[(\alpha ^ { * } \langle0|+\beta^{*}\langle 1|)(\alpha|0\rangle+\beta|1\rangle)=1 \quad \text { or } \quad|\alpha|^{2}+|\beta|^{2}=1\tag{2.1}\]

Esto se llama principio de superposición: cualquier superposición normalizada de estados cuánticos válidos vuelve a ser un estado cuántico válido. Es una consecuencia directa de la linealidad del espacio vectorial, y como veremos más adelante, este principio tiene algunas consecuencias extrañas que han sido corroboradas en muchos experimentos.

Utilizamos un sombrero para distinguir entre lo observable y el operador, pero generalmente esta distinción no es necesaria. En estas notas, usaremos sombreros sólo cuando exista peligro de confusión.

Como ejemplo, tomemos al operador\(X\):

\[X|0\rangle=|1\rangle \quad \text { and } \quad X|1\rangle=|0\rangle.\tag{2.2}\]

Este operador puede interpretarse como un bit flip de un qubit. En notación matricial los vectores de estado pueden escribirse como

\[|0\rangle=\left(\begin{array}{l}1 \\ 0 \end{array}\right) \quad \text { and } \quad|1\rangle=\left(\begin{array}{l} 0 \\ 1 \end{array}\right),\tag{2.3}\]

lo que significa que\(X\) está escrito como

\ [X=\ left (\ begin {array} {ll}
0 & 1\\
1 & 0
\ end {array}\ derecha)\ tag {2.4}\]

con valores propios ±1. Los autoestados de\(X\) son

\[|\pm\rangle=\frac{|0\rangle \pm|1\rangle}{\sqrt{2}}.\tag{2.5}\]

Estos estados forman una base ortonormal.

El valor de expectativa de\(A\) con respecto al estado del sistema\(|\psi\rangle\) se denota por\(\langle A\rangle\), y se evalúa como

\[\langle A\rangle=\langle\psi|A| \psi\rangle=\langle\psi|(\sum_{j} a_{j}|a_{j}\rangle\langle a_{j}|)| \psi\rangle=\sum_{j} p(a_{j}) a_{j}\tag{2.8}\]

Este es el promedio ponderado de los resultados de la medición. La dispersión de los resultados de la medición (o la incertidumbre) viene dada por la varianza

\[(\Delta A)^{2}=\left\langle(A-\langle A\rangle)^{2}\right\rangle=\left\langle A^{2}\right\rangle-\langle A\rangle^{2}\tag{2.9}\]

Hasta ahora nos ocupamos principalmente de sistemas discretos en espacios Hilbert de dimensiones finitas. Pero, ¿qué pasa con los sistemas continuos, como una partícula en una caja, o un oscilador armónico? Todavía podemos escribir la descomposición espectral de un operador A pero la suma debe ser reemplazada por una integral:

\[A=\int d a f_{A}(a)|a\rangle\langle a|\tag{2.10}\]

donde\(|a\rangle\) es un autoestado de\(A\). Por lo general, existen problemas con la normalización de\(|a\rangle\), lo que se relaciona con la imposibilidad de preparar un sistema exactamente en el estado\(|a\rangle\). No vamos a explorar más a fondo estas sutilezas en este curso, pero debes ser consciente de que existen. El valor de expectativa de\(A\) es

\[\langle A\rangle=\langle\psi|A| \psi\rangle=\int d a f_{A}(a)\langle\psi \mid a\rangle\langle a \mid \psi\rangle \equiv \int d a f_{A}(a)|\psi(a)|^{2},\tag{2.11}\]

donde definimos la función de onda\(\psi(a)=\langle a \mid \psi\rangle\), y\(|\psi(a)|^{2}\) se interpreta correctamente como la densidad de probabilidad que recuerdas de la mecánica cuántica de segundo año.

La probabilidad de encontrar el valor propio de un operador\(A\) en el intervalo\(a\) y\(a+d a\) dado el estado\(|\psi\rangle\) es

\[\langle\psi|(|a\rangle\langle a| d a)| \psi\rangle \equiv d p(a),\tag{2.12}\]

ya que ambos lados deben ser infinitesimales. Por lo tanto, encontramos que

\[\frac{d p(a)}{d a}=|\psi(a)|^{2}\tag{2.13}\]

Podemos escribir el estado de un sistema en el momento\(t\) como\(|\psi(t)\rangle\), y en algún momento\(t_{0}<t\) como\(\left|\psi\left(t_{0}\right)\right\rangle\). El cuarto postulado nos dice que hay un operador unitario\(U\left(t, t_{0}\right)\) que transforma el estado en el momento\(t_{0}\) al estado en el tiempo\(t\):

\[|\psi(t)\rangle=U\left(t, t_{0}\right)\left|\psi\left(t_{0}\right)\right\rangle\tag{2.14}\]

Dado que la evolución de tiempo\(t\) a\(t\) se denota por\(U(t, t)\) y debe ser igual a la identidad, deducimos que\(U\) depende sólo de las diferencias de tiempo:\(U\left(t, t_{0}\right)=U\left(t-t_{0}\right)\), y\(U(0)=\mathbb{I}\).

Como ejemplo,\(U(t)\) déjese generar por un operador hermitiano de\(A\) acuerdo con

\(U(t)=\exp \left(-\frac{i}{\hbar} A t\right)\tag{2.15}\)

El argumento de lo exponencial debe ser adimensional, por lo que\(A\) debe ser proporcional a\(\hbar\) veces una frecuencia angular (es decir, una energía). Supongamos que ese\(|\psi(t)\rangle\) es el estado de un qubit, y eso\(A=\hbar \omega X\). Si\(|\psi(0)\rangle=|0\rangle\) queremos calcular el estado del sistema en el momento\(t\). Podemos escribir

\[|\psi(t)\rangle=U(t)|\psi(0)\rangle=\exp (-i \omega t X)|0\rangle=\sum_{n=0}^{\infty} \frac{(-i \omega t)^{n}}{n !} X^{n}\tag{2.16}\]

Observe eso\(X^{2}=\mathbb{I}\), para que podamos separar la serie de potencias en valores pares e impares de n:

\[|\psi(t)\rangle=\sum_{n=0}^{\infty} \frac{(-i \omega t)^{2 n}}{(2 n) !}|0\rangle+\sum_{n=0}^{\infty} \frac{(-i \omega t)^{2 n+1}}{(2 n+1) !} X|0\rangle=\cos (\omega t)|0\rangle-i \sin (\omega t)|1\rangle\tag{2.17}\]

En otras palabras, el estado oscila entre\(|0\rangle\) y\(|1\rangle\).

El cuarto postulado también conduce a la ecuación de Schrödinger. Tomemos la forma infinitesimal de la Ec. (2.14):

\[|\psi(t+d t)\rangle=U(d t)|\psi(t)\rangle\tag{2.18}\]

Requerimos que\(U(d t)\) sea generado por algún operador hermitiano\(H\):

\[U(d t)=\exp \left(-\frac{i}{\hbar} H d t\right)\tag{2.19}\]

\(H\)debe tener las dimensiones de la energía, por lo que la identificamos con el operador energético, o el hamiltoniano. Ahora podemos llevar una expansión Taylor de\(|\psi(t+d t)\rangle\) a primer orden en dt:

\[|\psi(t+d t)\rangle=|\psi(t)\rangle+d t \frac{d}{d t}|\psi(t)\rangle+\ldots,\tag{2.20}\]

y ampliamos el operador unitario a primer orden en dt también:

\[U(d t)=1-\frac{i}{\hbar} H d t+\ldots\tag{2.21}\]

Combinamos esto en

\[|\psi(t)\rangle+d t \frac{d}{d t}|\psi(t)\rangle=\left(1-\frac{i}{\hbar} H d t\right)|\psi(t)\rangle,\tag{2.22}\]

que se puede reconvertir en la ecuación de Schrödinger:

\[i \hbar \frac{d}{d t}|\psi(t)\rangle=H|\psi(t)\rangle\tag{2.23}\]Por lo tanto, ¡la ecuación de Schrödinger sigue directamente de los postulados!

Este es el infame postulado de proyección, así llamado porque una medida “proyecta” el sistema al autoestado correspondiente al valor medido. Este postulado tiene como consecuencia observable que una segunda medición inmediatamente después de la primera también encontrará el resultado\(a_{j}\). Cada resultado de medición\(a_{j}\) corresponde a un operador de proyección\(P_{j}\) en el subespacio abarcado por el (los) vector (es) propio (es) perteneciente (s) a\(a_{j}\). Una medición (perfecta) se puede describir aplicando un proyector al estado, y renormalizar:

\[|\psi\rangle \rightarrow \frac{P_{j}|\psi\rangle}{\| P_{j}|\psi\rangle \|}\tag{2.24}\]

Esto también funciona para valores propios degenerados.

Hemos establecido anteriormente que el valor de expectativa de\(A\) puede escribirse como una traza:

\[\langle A\rangle=\operatorname{Tr}(|\psi\rangle\langle\psi| A)\tag{2.25}\]

Ahora, en lugar del operador completo\(A\), calculamos el rastro de\(P_{j}=\left|a_{j}\right\rangle\left\langle a_{j}\right|\):

\[\left\langle P_{j}\right\rangle=\operatorname{Tr}\left(|\psi\rangle\langle\psi| P_{j}\right)=\operatorname{Tr}\left(|\psi\rangle\left\langle\psi \mid a_{j}\right\rangle\left\langle a_{j}\right|\right)=\left|\left\langle a_{j} \mid \psi\right\rangle\right|^{2}=p\left(a_{j}\right)\tag{2.26}\]

Así podemos calcular la probabilidad de un resultado de medición tomando el valor de expectativa del operador de proyección que corresponde al estado propio del resultado de la medición. Este es uno de los cálculos básicos en mecánica cuántica que deberías poder hacer.

El problema de la medición

El postulado de proyección es algo problemático para la interpretación de la mecánica cuántica, porque conduce al llamado problema de medición: ¿Por qué una medición induce una evolución no unitaria del sistema? Después de todo, el aparato de medición también se puede describir cuántico mecánicamente ² y luego el sistema más el aparato de medición evoluciona unitariamente. Pero entonces debemos invocar un nuevo dispositivo que mida el sistema combinado y el aparato de medición. Sin embargo, esto a su vez puede describirse cuántico mecánicamente, y así sucesivamente.

Por otro lado, sí vemos resultados de medición definidos cuando hacemos experimentos, por lo que en algún nivel el postulado de proyección es necesario, y en algún lugar debe haber un “colapso de la función de onda”. Schrödinger ya luchó con esta pregunta, y se le ocurrió su famoso experimento de pensamiento sobre un gato en una caja con un vial lleno de veneno unido a un contador Geiger monitoreando un átomo radiactivo (Figura 1). Cuando el átomo decae, activará el contador Geiger, lo que a su vez provoca la liberación del veneno matando al gato. Cuando no miramos dentro de la caja (más precisamente: cuando ninguna información sobre el sistema atom-contra-vial-gato escapa de la caja), todo el sistema está en una superposición cuántica. No obstante, cuando abrimos la caja, sí encontramos al gato vivo o muerto. Una solución del problema parece ser que el estado cuántico representa nuestro conocimiento del sistema, y que mirar dentro de la caja simplemente actualiza nuestra información sobre el átomo, contador, vial y el gato. Entonces nada “colapsa” excepto nuestro propio estado de ánimo.

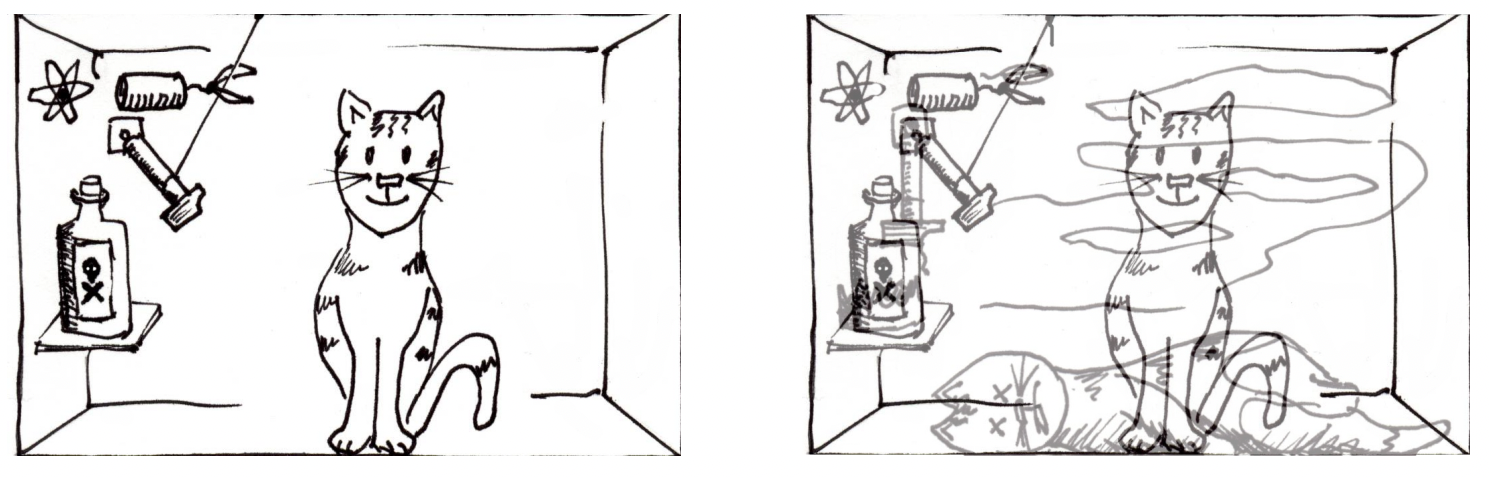Figura 1: Schrödingers Cat.

Sin embargo, esta no puede ser toda la historia, porque la mecánica cuántica claramente no se trata solo de nuestras opiniones sobre los gatos y los átomos en descomposición. En particular, si preparamos un electrón en un estado de spin “up”\(|\uparrow\rangle\), entonces cada vez que medimos el giro a lo largo de la\(z\) -dirección encontraremos el resultado de la medición “arriba”, sin importar lo que pensemos sobre los electrones y la mecánica cuántica. Entonces parece haber alguna propiedad física asociada al electrón que determina el resultado de la medición y es descrita por el estado cuántico.

Diversas interpretaciones de la mecánica cuántica intentan abordar estas (y otras) cuestiones. La interpretación original de la mecánica cuántica fue presentada principalmente por Niels Bohr, y se llama la interpretación de Copenhague. En términos generales, dice que el estado cuántico es una ficción conveniente, utilizada para calcular los resultados de los resultados de medición, y que el sistema no puede considerarse separado del aparato de medición. Alternativamente, hay interpretaciones de la mecánica cuántica, como la interpretación de Ghirardi-Rimini-Weber, que sí atribuyen algún tipo de realidad al estado del sistema, en cuyo caso se debe dar un mecanismo físico para el colapso de la función de onda. Muchas de estas interpretaciones pueden clasificarse como teorías de variables ocultas, que postulan que existe una realidad física más profunda descrita por algunas “variables ocultas” que debemos promediar. Esto a su vez explica la naturaleza probabilística de la mecánica cuántica. El problema con tales teorías es que estas variables ocultas deben ser bastante raras: pueden cambiar instantáneamente dependiendo de eventos a años luz de distancia3, violando así la teoría de la relatividad especial de Einstein. A muchos físicos no les gusta este aspecto de las teorías de variables ocultas.

Alternativamente, la mecánica cuántica puede interpretarse en términos de “muchos mundos”: la interpretación de Muchos Mundos establece que hay un vector de estado para todo el universo, y que cada medición divide el universo en diferentes ramas correspondientes a los diferentes resultados de medición. Es atractivo ya que parece ser una interpretación filosóficamente consistente, y si bien ha ido adquiriendo un número creciente de seguidores en los últimos años ⁴, muchos físicos tienen una profunda aversión a la idea de universos paralelos.

Por último, está la interpretación epistémica, que es muy similar a la interpretación de Copenhague en que trata al estado cuántico en gran medida como una medida de nuestro conocimiento del sistema cuántico (y del aparato de medición). Al mismo tiempo, niega una realidad subyacente más profunda (es decir, no hay variables ocultas). La característica atractiva de esta interpretación es que requiere una cantidad mínima de alboroto, y encaja naturalmente con la investigación actual en la teoría de la información cuántica. El inconveniente es que hay que abandonar el simple realismo científico que permite hablar de las propiedades de los electrones y los fotones, y muchos físicos no están preparados para hacerlo.

Como puede ver, la mecánica cuántica nos obliga a abandonar algunas convicciones profundamente arraigadas (clásicas) sobre la Naturaleza. Dependiendo de su preferencia, puede sentirse atraído por una u otra interpretación. Actualmente no se sabe cuál interpretación es la correcta.

Ejercicios

1. Calcular los valores propios y los estados propios del operador de cambio de bits\(X\), y mostrar que los autoestados forman una base ortonormal. Calcular el valor de expectativa de\(X\) for\(|\psi\rangle=1 / \sqrt{3}|0\rangle+i \sqrt{2 / 3}|1\rangle\).
2. Demostrar que la varianza de\(A\) desaparece cuando\(|\psi\rangle\) es un estado propio de\(A\).
3. Demostrar que un operador es hermitiano si y sólo si tiene valores propios reales.
4. Demostrar que no se\(|\psi\rangle\) puede copiar un qubit en estado desconocido. Este es el teorema de no clonación. Pista: comenzar con un estado\(|\psi\rangle|i\rangle\) para algún estado inicial\(|i\rangle\), y requieren que para\(|\psi\rangle=|0\rangle\) y\(|\psi\rangle=|1\rangle\) el procedimiento de clonación sea una transformación unitaria\(|0\rangle|i\rangle \rightarrow|0\rangle|0\rangle\) y\(|1\rangle|i\rangle \rightarrow|1\rangle|1\rangle\).
5. El principio de incertidumbre.
   1. Utilice la desigualdad Cauchy-Schwarz para derivar la siguiente relación entre observables no desplazamientos\(A\) y\(B\):

      \[(\Delta A)^{2}(\Delta B)^{2} \geq \frac{1}{4}|\langle[A, B]\rangle|^{2}\tag{2.27}\]

      Pista: definir\(|f\rangle=(A-\langle A\rangle)|\psi\rangle\) y\(|g\rangle=i(B-\langle B\rangle)|\psi\rangle\), y usar eso\(|\langle f \mid g\rangle| \geq \frac{1}{2} \mid\langle f \mid g\rangle+\langle g|f\rangle|\).

   2. Demostrar que esto reduce a la relación de incertidumbre de Heisenberg cuando\(A\) y\(B\) son observables conjugados canónicamente, por ejemplo posición e impulso.
   3. ¿Funciona este método para derivar el principio de incertidumbre entre la energía y el tiempo?
6. Consideremos al hamiltoniano\(H\) y al estado\(|\psi\rangle\) dado por

   \ [H=E\ left (\ begin {array} {ccc}
   0 & i & 0\\
   -i & 0 & 0\\
   0 & 0 & -1
   \ end {array}\ derecha)\ quad\ text {y}\ quad|\ psi\ rangle=\ frac {1} {\ sqrt {5}}\ left (\ begin {array} {c}
   1-i\\
   1-i \\
   1
   \ end {array}\ derecha)\ tag {2.28}\]

   donde\(E\) es una constante con dimensiones de energía. Calcular los valores propios de energía y el valor de expectativa del hamiltoniano.

7. Demostrar que el impulso y la energía total se pueden medir simultáneamente solo cuando el potencial es constante en todas partes. ¿Qué significa un potencial constante en términos de la dinámica de una partícula?

---

¹ En los espacios Hilbert de dimensionalidad infinita, existen sutiles diferencias entre los operadores autounidos y hermitianos. Aquí ignoramos estas sutilezas, porque en su mayoría estaremos tratando con espacios finito-dimensionales.

² Esto es algo que la mayoría de la gente requiere de una teoría fundamental: la mecánica cuántica no debe simplemente descomponerse para objetos macroscópicos. En efecto, se ha encontrado evidencia experimental de superposiciones macroscópicas en forma de “estados de gato”.

^3.. a pesar de que el promedio sobre las variables ocultas significa que nunca se puede señalar más rápido que la luz.

⁴ Parece haber alguna evidencia de que la interpretación de Muchos Mundos encaja bien con los últimos modelos cosmológicos basados en la teoría de cuerdas