Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

24.2: Péndulo Físico

Última actualización

30 oct 2022
Guardar como PDF
- 24.1: Introducción a los Péndulos Físicos
- 24.3: Ejemplos trabajados

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Un péndulo físico consiste en un cuerpo rígido que se somete a rotación de eje fijo alrededor de un punto fijo $S$ (Figura 24.2).

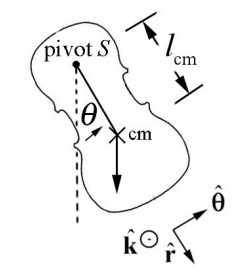
La fuerza gravitacional actúa en el centro de masa del péndulo físico. Denote la distancia del centro de masa al punto de pivote $S$ por $l_{\mathrm{cm}}$ . El análisis de par es casi idéntico al péndulo simple. El par sobre el punto de pivote $S$ viene dado por

$\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, \mathrm{cm}} \times m \overrightarrow{\mathrm{g}}=l_{\mathrm{cm}} \hat{\mathbf{r}} \times m g(\cos \theta \hat{\mathbf{r}}-\sin \theta \hat{\boldsymbol{\theta}})=-l_{\mathrm{cm}} m g \sin \theta \hat{\mathbf{k}} \nonumber$

Siguiendo los mismos pasos que llevaron de la Ecuación (24.1.1) a la Ecuación (24.1.4), la ecuación rotacional para el péndulo físico es

$-m g l_{\mathrm{cm}} \sin \theta=I_{S} \frac{d^{2} \theta}{d t^{2}} \nonumber$

donde $I_{s}$ el momento de inercia sobre el punto de pivote $S$ . Al igual que con el péndulo simple, para ángulos pequeños $\sin \theta \approx \theta$ , la ecuación (24.2.2) se reduce a la ecuación del oscilador armónico simple

$\frac{d^{2} \theta}{d t^{2}} \simeq-\frac{m g l_{\mathrm{cm}}}{I_{S}} \theta \nonumber$

La ecuación para el ángulo $\theta(t)$ viene dada por

$\theta(t)=A \cos \left(\omega_{0} t\right)+B \sin \left(\omega_{0} t\right) \nonumber$

donde la frecuencia angular viene dada por

$\omega_{0} \simeq \sqrt{\frac{m g l_{\mathrm{cm}}}{I_{S}}} \quad(\text { physical pendulum }) \nonumber$

y el periodo es

$T=\frac{2 \pi}{\omega_{0}} \simeq 2 \pi \sqrt{\frac{I_{S}}{m g l_{\mathrm{cm}}}} \quad(\text { physical pendulum }) \nonumber$

Sustituir el teorema del eje paralelo, $I_{S}=m l_{\mathrm{cm}}^{2}+I_{\mathrm{cm}}$ en la Ecuación (24.2.6) con el resultado de que

$T \simeq 2 \pi \sqrt{\frac{l_{\mathrm{cm}}}{g}+\frac{I_{\mathrm{cm}}}{m g l_{\mathrm{cm}}}} \quad(\text { physical pendulum }) \nonumber$

Así, si el objeto es “pequeño” en el sentido de que $I_{\mathrm{cm}}<<m l_{\mathrm{c}}^{2}$ , las expresiones para el péndulo físico se reducen a las del péndulo simple. El componente z de la velocidad angular viene dado por

$\omega_{z}(t)=\frac{d \theta}{d t}(t)=-\omega_{0} A \sin \left(\omega_{0} t\right)+\omega_{0} B \cos \left(\omega_{0} t\right) \nonumber$

Los coeficientes A y B se pueden determinar a partir de las condiciones iniciales estableciendo t = 0 en las Ecuaciones (24.2.4) y (24.2.8) dando como resultado las condiciones que

\ [\ begin {array} {l}
A=\ theta (t=0)\ equiv\ theta_ {0}\\
B=\ frac {\ omega_ {z} (t=0)} {\ omega_ {0}}\ equiv\ frac {\ omega_ {z, 0}} {\ omega_ {0}}
\ end {nonarray}\ umber\]

Por lo tanto, las ecuaciones para el ángulo $\theta(t) \text { and } \omega_{z}(t)=\frac{d \theta}{d t}(t)$ vienen dadas por

\ [\ begin {array} {c}
\ theta (t) =\ theta_ {0}\ cos\ izquierda (\ omega_ {0} t\ derecha) +\ frac {\ omega_ {z, 0}} {\ omega_ {0}}\ sin\ izquierda (\ omega_ {0} t\ derecha)\
\ omega_ {z} (t)\ frac {d\ theta} {d t} (t) =-\ omega_ {0}\ theta_ {0}\ sin\ izquierda (\ omega_ {0} t\ derecha) +\ omega_ {z, 0}\ cos\ izquierda (\ omega_ {0} t\ derecha)
\ end {array}\ nonumber\]

Support Center

How can we help?