2.20: Elipses y Elipsoides

Aquí hay algunos problemas relacionados con elipses y elipsoides que podrían ser de interés.

Determinar los principales momentos de inercia de los siguientes:

1. Una lámina plana uniforme de masa$m$ en forma de elipse de semiejes$a$ y$b$.
2. Un anillo plano uniforme de masa$m$ en forma de elipse de semiejes$a$ y$b$.
3. Un elipsoide triaxial sólido uniforme de masa$m$ y semiejes$a, b$ y$c$.
4. Un elipsoide triaxial hueco uniforme de masa$m$ y semiejes$a, b$ y$c$.

1. Por integración, una lámina elíptica es un poco difícil, ¡pero por perspicacia física es muy fácil!

La distribución de la masa alrededor del eje menor es la misma que para una lámina circular de radio$a$, y por lo tanto el momento$B$ es el mismo que para la lámina circular, es decir$B = \frac{1}{4} ma^2$. De igual manera$A = \frac{1}{4} mb^2$,, y por ende, por el teorema de ejes perpendiculares,$C = \frac{1}{4} m(a^2 + b^2 )$.

Creo que encontrarás que la forma de la elipse momental es la misma que la forma de la lámina elíptica original.

2. Un anillo elíptico (aro) es notablemente difícil. No puede expresarse en términos de funciones elementales, y tiene que calcularse numéricamente. Se puede expresar en términos de integrales elípticas (no es de sorprender allí), pero la mayoría de nosotros no estamos seguros de qué son las integrales elípticas y apenas cuentan como funciones elementales, y de todos modos tienen que calcularse numéricamente. Tomamos la elipse para estar$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,$ con$b≤a$.

Incluso calcular la circunferencia de una elipse no es tan fácil. La circunferencia es

$\oint ds = 4 \int_{0}^{a} [ 1 + (\frac{dy}{dx} )^2] dx$, con$y = b ( 1 - \frac{x^2}{a^2} )^\frac{1}{2}$.

Después de un poco de álgebra, esto se puede escribir como

$\frac{4a}{x} \int_{0}^{a} \sqrt{\frac{c^2 -x^2}{a^2 - z^2}}dx$, donde$c^2 = \frac{a^4}{a^2 - b^2}$.

Al principio esto parece fácil, pero no creo que puedas hacerlo en cuanto a funciones elementales. No hay problema, entonces — solo integrarlo numéricamente. Desafortunadamente el integrando se vuelve infinito en el límite superior, por lo que todavía hay un pequeño problema. Sin embargo, un cambio de variable para$x = a \sin \theta$ resolver ese problema. La expresión de la circunferencia se vuelve simplemente

$4a\int_{0}^{\pi /2 } [1 - (\frac{a^2 - b^2}{a^2}) \sin ^2 \theta ]^\frac{1}{2} d \theta$,

que se puede integrar numéricamente sin problemas infinitos en los límites. Según mis cálculos, la circunferencia de la elipse es$ha$, donde$h$ es una función de$b/a$ lo siguiente:

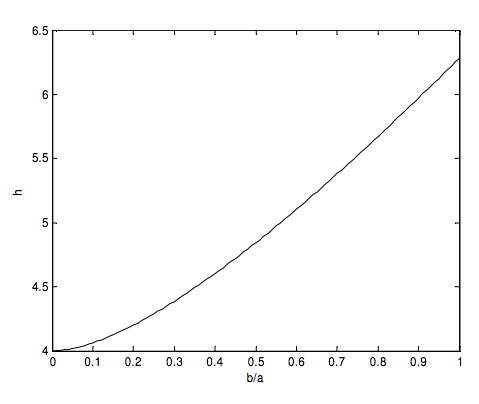
Para encontrar el momento de inercia (o el segundo momento de longitud) alrededor del eje menor, tenemos que multiplicar el integrando por$x^2$, o$a^2 \sin^2 \theta$, e integrar. Así es el momento de inercia del aro elíptico alrededor de su eje menor$c_1ma^2$, donde

\ (c_1 =\ frac {\ int_ {0} ^ {\ pi/2} [1 - (\ frac {a^2 - b^2} {a^2})\ sin^2\ theta] ^ {1/2}\ sin^2
\ theta d\ theta} {\ int_ {0} ^ {\ pi/2} [1- (\ frac {a^2 - b^2} {a^2})\ sen ^2\ theta] ^ {1/2} d\ theta}\)

El momento de inercia sobre el eje mayor es$c_2ma^2$, donde

$c_2 = \frac{ \frac{b^2}{a^2}\int_{0}^{\pi / 2 } [1 - ( \frac{a^2 - b^2}{a^2} ) cos^2]^{1/2} \sin^2 \theta d \theta }{ \int_{0}^{\pi / 2 } [ 1- (\frac{a^2 - b^2}{a^2} )\sin^2 \theta ]^{1/2} d \theta}$

Estos dos coeficientes de$ma^2$ se muestran a continuación en función de$b/a$.

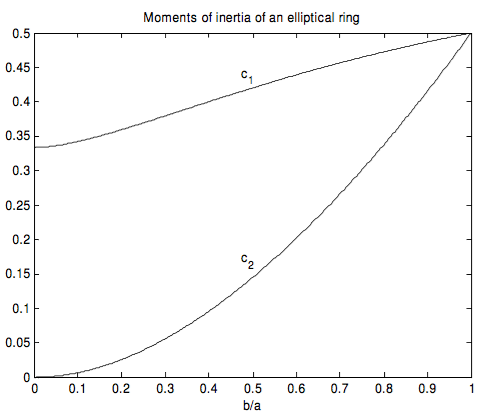
Los momentos de inercia de un anillo elíptico de masa$m$ y ejes semi mayores y semi menores$a$ y$b$ son$c_1ma^2$ alrededor del eje menor y$c_2ma^2$ alrededor del eje mayor, donde$c_1$ y se$c_2$ muestran como funciones de$b/a$.

El momento de inercia alrededor del eje mayor también se puede expresar convenientemente en términos de$b$ más que$a$. Si escribimos el momento de inercia sobre el eje mayor como$c_4mb^2$, entonces$c_4$ como una función de$b/a$ se muestra a continuación.

El momento de inercia alrededor de un eje perpendicular al plano de la elipse y que pasa por su centro es$c_3ma^2$, donde, por supuesto (por el teorema de ejes perpendiculares),$c_3 = c_1 + c_2$.

También es igual a$c_1ma^2 + c_4mb^2$.

3. Para un elipsoide triaxial sólido uniforme, los momentos de inercia son

$A = \frac{1}{5} m(b^2 + c^2) \qquad B = \frac{1}{5} m(c^2 + a^2) \qquad C = \frac{1}{5} m(c^2 + a^2)$

El elipsoide momental no es de la misma forma. Sus ejes están en la relación

Por ejemplo, si las relaciones axiales del elipsoide original son 1:2:3, las relaciones axiales del elipsoide momental correspondiente es$1 : \sqrt{\frac{13}{10}} : \sqrt{\frac{13}{5}} = 1 : 1.140 : 1.612$, que es ligeramente más esférico que el elipsoide original.

4. Carcasa elíptica triaxial. Tenemos que pensar detenidamente qué es un caparazón elíptico triaxial. Si imaginamos que la superficie interna de la concha es un elipsoide, y la superficie externa un elipsoide similar, pero con todas las dimensiones lineales aumentadas en el mismo pequeño incremento fraccional, entonces obtenemos una figura como esta:

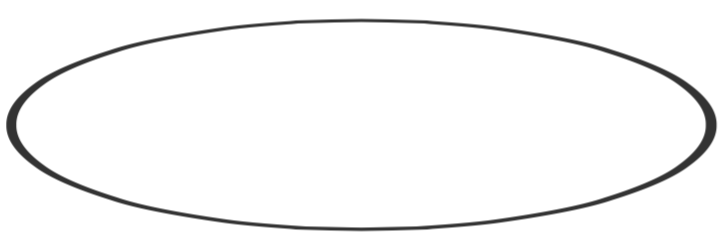
En este dibujo el tamaño lineal de la superficie exterior es 3 por ciento mayor que el de la superficie interna. E. J. Routh muestra correctamente en su tratado sobre cuerpos rígidos que son los principales momentos de inercia de tal figura$\frac{1}{3} m(b^2 + c^2), \frac{1}{3} m(c^2 + a^2), \frac{1}{3}m(a^2 + b^2)$.

Pero se puede ver que tal figura no es (como presumiblemente es una bola rugger) de espesor uniforme. Dibujo debajo un caparazón de espesor uniforme. En tal caso las superficies interna y externa no son exactamente similares.

Al intentar calcular el momento de inercia de tal figura me limitaré al caso de una concha esferoidal de espesor uniforme. Es decir, un elipsoide con dos ejes iguales, representados por la ecuación, en coordenadas cilíndricas

$\frac{\rho^2}{a^2} + \frac{z^2}{c^2} = 1,$

donde$\rho^2 = x^2 + y^2$. Además, si pongo$c = \chi a$, se puede escribir la ecuación al esferoide

$\rho^2 + \frac{z^2}{\chi^2} = a^2,$

Si$\chi < 1$, el esferoide es oblato. Si$\chi > 1$, el esferoide es prolado.

Primero tendremos que calcular su superficie, que es

$A = 4 \pi \int_{0}^{c} \rho [ 1 + (\frac{d\rho}{dz})^2]^\frac{1}{2} dz$

Después de un poco de álgebra, esto llega a

$A = 4 \pi a^2 f (\chi ),$

donde

$f (\chi ) = \dfrac{1}{2}\left[\frac{\chi^2}{\sqrt{1 - \chi^2}} \ln \left( \dfrac{1 + \sqrt{1 - \chi^2}}{\chi}\right)+1\right]$para$\chi \leq 1$

y

$f (\chi ) = \dfrac{1}{2}\left[\frac{\chi^2}{\sqrt{\chi^2-1}} \sin^{-1}\left( \dfrac{\sqrt{\chi^2-1}}{\chi}\right)+1\right]]$para$\chi \geq 1$

Esta función se muestra a continuación en cuanto a$\chi = 2$. Para$\chi = 0$, la cifra es un disco cuya superficie total

(superficie superior e inferior) es$2 \pi a^2$, y$f = \frac{1}{2}$. Porque$\chi = 1$, la figura es una esfera cuya área es$4 \pi a^2$, y$f = 1$. La función va al infinito como$\chi$ va al infinito.

El momento de inercia alrededor del$z$ eje es

$I = \frac{4 \pi m }{A}\int_{0}^{c} \rho ^3 [ 1 +(\frac{d \rho}{dz})^2]^{1/2} dz.$

Después de algo de álgebra esto se convierte

$I = ma^2 g ( \chi )$

$g ( \chi ) = \frac{(2-\chi ^2) (1-\chi ^2) - \chi^4 \ln\left[\left(1 + \sqrt{1- \chi^2}\right)/ \chi\right]}{4 \left\{ (1- \chi^2)^{3/2} + \chi^2 (1-\chi^2) \ln\left[(1 + \sqrt{1- \chi^2})/ \chi \right]\right\} }$para$\chi \leq 1$

$g (\chi) = 1 - \frac{\frac{\chi^4}{(\chi - 1)^{3/2}}sin^{-1}\left(\frac{\sqrt{\chi^2-1}}{\chi}\right)+\frac{\chi^2 -2}{\chi^2 -1 }}{4 \left\{ \frac{\chi^2}{\sqrt{\chi^2-1}}sin^{-1}\left(\frac{\sqrt{\chi^2-1}}{\chi}\right) +1 \right\}}$para$\chi \geq 1$

Esta función se muestra a continuación en cuanto a$\chi = 2$ For$\chi = 0$, la figura es un disco cuyo momento de inercia es$\frac{1}{2} \pi a^2$, y$f = \frac{1}{2}$. Porque$\chi = 1$, la figura es una esfera hueca cuyo momento de inercia es$\frac{2}{3} \pi a^2$, y$f = \frac{2}{3}$. La función va a 1 como$\chi$ va al infinito; el momento de inercia se acerca entonces al de un cilindro hueco.