3.2: Momento de Fuerza

Primero, veamos una situación bidimensional familiar. En la Figura III.1 dibujo una fuerza$\textbf{F}$ y un punto O. El momento de la fuerza con respecto a O puede definirse como

Fuerza tiempos perpendiculares distancia de O a la línea de acción de$\textbf{F}$.

Alternativamente, (Figura III.2) el momento puede definirse igualmente bien por

Componente transversal de la fuerza tiempos distancia desde O hasta el punto de aplicación de la fuerza.

De cualquier manera, la magnitud del momento de la fuerza, también conocida como el par, es$rF \sin\theta$ Podemos considerarla como un vector$\boldsymbol\tau$,, perpendicular al plano del papel:

\ begin {ecuación}\\ negridsymbol\ tau =\ textbf {r}\ times\ textbf {F}\ tag {3.2.1}\ label {eq:3.2.1}\ end {ecuación}

Ahora déjenme hacer una pregunta. ¿Es correcto decir el momento de una fuerza con respecto a (o “sobre”) un punto o con respecto a (o “alrededor”) de un eje?

En el ejemplo bidimensional anterior, no importa, pero ahora permítanme pasar a tres dimensiones, y trataré de aclarar.

En la Figura III.3, dibujo un conjunto de ejes rectangulares, y una fuerza$\textbf{F}$, cuyo vector de posición con respecto al origen es$\textbf{r}$.

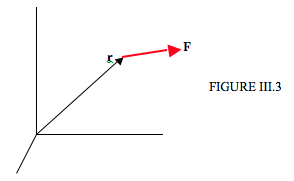
El momento, o par, de$\textbf{F}$ con respecto al origen es el vector

\ begin {ecuación}\\ negridsymbol\ tau =\ textbf {r}\ times\ textbf {F}\ tag {3.2.2}\ label {eq:3.2.2}\ end {ecuación}

Los componentes$x-, y-$ y$z$ - de$\boldsymbol\tau$ son los momentos de$\textbf{F}$ con respecto a los ejes$x-, y-$ y z. Puede encontrar fácilmente los componentes de$\boldsymbol\tau$ expandiendo el producto cruzado$\ref{eq:3.2.2}$:

$$\boldsymbol\tau = \hat{\textbf{x}}(yF_{z}-zF_{y})+\hat{\textbf{y}}(yF_{x}-xF_{z})+\hat{\textbf{z}}(xF_{y}-yF_{x}) \tag{3.2.3}\label{eq:3.2.3}$$

donde$\bf \hat{x},\hat{y},\hat{z}$ están los vectores unitarios a lo largo de los$x,y,z$ ejes. En la Figura III.4, estamos mirando hacia abajo el$x$ -eje, y he dibujado los componentes$F_{y}$ y$F_{z}$, y se puede ver que, efectivamente,$\tau_{x} =yF_{z}-zF_{y}$.

Las dimensiones de momento de una fuerza, o par, son ML ² T ^{- 2}, y las unidades SI son N m. (Lo mejor es dejar las unidades como N m en lugar de expresar el par en julios).