12.1: La cuerda en tres dimensiones

En la mayoría de nuestras discusiones sobre los fenómenos de las olas hasta el momento, hemos asumido que la moción se está llevando a cabo en un plano, para que podamos dibujar imágenes del sistema en una hoja de papel. Nos hemos estado limitando implícitamente a ondas bidimensionales. Esto está bien para oscilaciones longitudinales en tres dimensiones, porque toda la acción se está llevando a cabo a lo largo de una sola línea. Sin embargo, para las oscilaciones transversales, pasar de dos dimensiones a tres dimensiones hace una enorme diferencia porque hay dos direcciones transversales en las que el sistema puede oscilar.

Por ejemplo, considere una cuerda en tres dimensiones, estirada en la\(z\) dirección. Cada punto de la cuerda puede oscilar tanto en la\(x\) dirección como en la\(y\) dirección. Si el sistema no fuera aproximadamente lineal, esto podría ser un problema horrendo. La linealidad nos permite resolver el problema de la oscilación en el\(x\)\(z\) plano por separado del problema de la oscilación en el\(y\)\(z\) plano. Ya hemos resuelto estos problemas bidimensionales en el capítulo 5. Entonces podemos simplemente juntar los resultados para obtener el movimiento más general del sistema tridimensional. En otras palabras, podemos tratar el\(x\) componente de la oscilación transversal y el\(y\) componente como completamente independientes.

Supongamos que hay una onda armónica que viaja en la\(z\) dirección + en la cuerda. El desplazamiento de la cuerda\(z\) desde su posición de equilibrio,\((0, 0, z)\), puede escribirse como\[\vec{\Psi}(z, t)=\operatorname{Re}\left[\left(\psi_{1} \hat{x}+\psi_{2} \hat{y}\right) e^{i(k z-\omega t)}\right]\]

donde\(\hat{x}\) y\(\hat{y}\) son vectores unitarios en la\(y\) dirección\(x\) y\(\psi_{1}\) y y\(\psi_{2}\) son parámetros complejos que describen la amplitud y fase de las oscilaciones en el\(x\)\(z\) plano y el\(y\)\(z\) plano,\[\psi_{j}=A_{j} e^{i \phi_{j}} \text { for } j=1 \text { to } 2.\]

Es conveniente organizar estos parámetros en un vector complejo\ [Z=\ left (\ begin {array} {l}
\ psi_ {1}\
\ psi_ {2}
\ end {array}\ right),\]

que da una descripción completa del movimiento de la cuerda.

Polarización

12-1

“Polarización” se refiere a la naturaleza del movimiento de un punto en la cuerda (u otra oscilación transversal). Esta moción está animada en el programa 12-1. Es posible que desee leer la discusión a continuación con este programa funcionando.

Si\(\phi_{1}=\phi_{2}\), o\(A_{1}\) o\(A_{2}\) es cero, entonces (12.3) representa una cadena linealmente polarizada. La polarización lineal es fácil de entender. Significa que cada punto de la cuerda oscila de un lado a otro en un plano fijo. Por ejemplo,\ [u_ {1} =\ left (\ begin {array} {l}
1\\
0
\ end {array}\ right)\]
\ [u_ {2} =\ left (\ begin {array} {l}
0\\
1
\ end {array}\ right)\]

representan cadenas que oscilan en el\(z\) plano\(x\) - y el\(z\) plano\(y\) - respectivamente. Una cadena que oscila en un plano un ángulo\(\theta\) desde el\(x\) eje positivo (hacia el\(y\) eje positivo) está representada por\ [u_ {\ theta} =\ left (\ begin {array} {l}
\ cos\ theta\
\ sin\ theta
\ end {array}\ right).\]

Esto se muestra en el\(y\) plano\(x\) - en la Figura\( 12.1\). Los vectores de polarización (12.4) - (12.6) se pueden multiplicar por un factor de fase\(e^{i \phi}\), sin afectar el estado de polarización de ninguna manera importante. Esto solo corresponde a un reajuste general del reloj.

Figura\( 12.1\):\(u_{1}\),\(u_{2}\) y\(u_{\theta}\).

Más interesante es la polarización circular. Una onda polarizada circularmente en una cadena está representada por\ [\ left (\ begin {array} {l}
1\\
i
\ end {array}\ right)\]

o\ [\ left (\ begin {array} {c}
1\\
-i
\ end {array}\ right).\]

En (12.7), el\(y\) componente se queda atrás del\(x\) componente por\(\pi / 2\left(=\phi_{2}\right)\). Así, en cualquier punto fijo en el espacio, el campo gira de\(x\) a\(y\), o en sentido contrario a las agujas del reloj visto desde el\(z\) eje positivo (con la onda viniendo hacia usted), como se muestra en la Figura\( 12.2\). A esto se le llama “polarización circular izquierda” porque la cuerda se asemeja a un tornillo zurdo. Asimismo,\ [\ left (\ begin {array} {c}
1\\
-i
\ end {array}\ right).\]

representa la rotación de la cuerda en sentido horario. A esto se le llama “polarización circular derecha”.

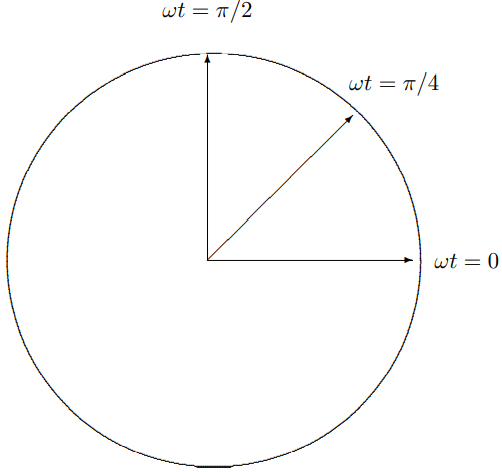
Figura\( 12.2\): Polarización circular.

El vector\ [\ left (\ begin {array} {c}
A\\
i B
\ end {array}\ right)\]

con\(A > B > 0\) representa polarización elíptica. Un punto en la cuerda traza una elipse con semieje mayor\(A\) a lo largo del eje 1 y semi-eje menor\(B\) a lo largo del eje 2, con rotación en sentido antihorario, como se muestra en la Figura\( 12.3\)

Figura\( 12.3\): Polarización elíptica con eje largo en la\(x\) dirección.

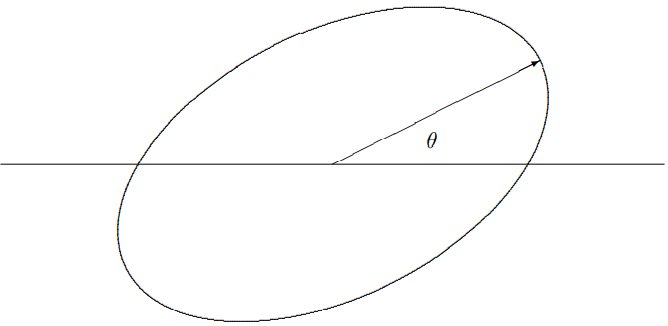
Figura\( 12.4\): Polarización elíptica general.

Se puede escribir un vector completamente general de la siguiente forma:\ [\ left (\ begin {array} {l}
\ psi_ {1}\\
\ psi_ {2}
\ end {array}\ right) =e^ {i\ phi}\ left (\ begin {array} {c}
A\ cos\ theta-i B\ sin\ theta\
A\ sin\ theta+i B\ cos\ theta
\ end {array}\ derecha)\]

con\(A \geq|B|\) y\(0 \leq \theta<\pi\) y\(\phi\) es fase real (que no es muy relevante para la física pero puede estar ahí para hacer que las matemáticas se vean más feas). Esto representa polarización elíptica con semieje mayor\(A\) en un ángulo\(\theta\) con el eje 1, como en\ [u_ {\ theta} =\ left (\ begin {array} {c}
\ cos\ theta\
\ sin\ theta
\ end {array}\ right).\]

y semieje menor\(B\) como se muestra en la Figura\( 12.4\). Si\(B\) es positivo (negativo), la rotación es en sentido antihorario (en sentido horario). Los parámetros físicamente interesantes\(A\),\(B\) y se\(\theta\) pueden encontrar de\(\psi_{1}\) y de la\(\psi_{2}\) siguiente manera:\ [\ begin {reunió}
A^ {2} +B^ {2} =\ izquierda|\ psi_ {1}\ derecha|^ {2} +\ izquierda|\ psi_ {2}\ derecha|^ {2},\\
A B=-\ operatorname {Im}\ left (\ psi_ {1}\ psi_ {2} ^ {*}\ derecha).
\ end {reunido}\]

Por lo tanto,\[A \pm B=\sqrt{\left|\psi_{1}\right|^{2}+\left|\psi_{2}\right|^{2} \mp 2 \operatorname{Im}\left(\psi_{1} \psi_{2}^{*}\right)} ,\]

da\(A\) y\(B\). Entonces\(\theta\) satisface\ [\ comenzar {alineado}
&\ izquierda (A^ {2} -B^ {2}\ derecha)\ cos 2\ theta=\ izquierda|\ psi_ {1}\ derecha|^ {2} -\ izquierda|\ psi_ {2}\ derecha|^ {2},\\
&\ izquierda (A^ {2} -B^ {2}\ derecha)\ sin 2\ theta=2\ nombreoperador {Re}\ izquierda (\ psi_ {1}\ psi_ {2} ^ {*}\ derecha).
\ end {alineado}\]

Observe que el factor de fase general se\(e^{i \phi}\) cancela en (12.11) - (12.13).