4.1.1: Ondas Transversales

Las olas se mueven con el tiempo, lo que dificulta dibujar en una hoja de papel. Hay dos posibles representaciones. Supongamos que hay un corcho flotando en el agua que se fija en un lugar determinado y registramos el desplazamiento (qué tan alto y bajo es desde el equilibrio) en diferentes momentos. Si trazamos el desplazamiento versus tiempo tenemos una gráfica de posición congelada:

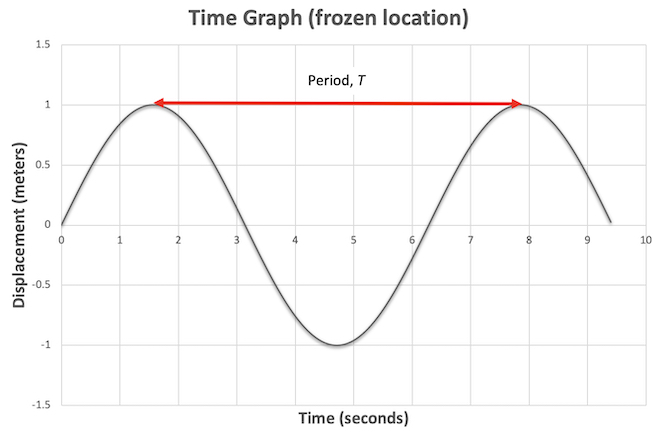
Figura\(\PageIndex{1}\)

El desplazamiento desde la posición de equilibrio se medirá en metros pero la distancia horizontal pico a pico es una medida de tiempo. Esta gráfica se parece a la gráfica de movimiento armónico simple del Capítulo 3. De hecho el corcho está experimentando un simple movimiento armónico y la distancia horizontal pico a pico en el es el periodo,\(T\) de la onda (al igual que la distancia pico a pico de un gráfico de tiempo de movimiento armónico fue el período). De acuerdo con la gráfica el primer pico está en\(1.5\text{ s}\) cuando el segundo está en\(7.8\text{ s}\) así que el periodo es\(7.8\text{ s} - 1.5\text{ s} = 6.3\text{ s}\). Al igual que en los dos últimos capítulos, la frecuencia de onda viene dada por\(f=1/T\) en Hertz por lo que esta oscilación tiene una frecuencia de\(1/6.3\text{ s} = 0.16\text{ Hz}\).

Podemos hacer un segundo tipo de gráfico de la onda si tomamos una instantánea (tiempo congelado) de la ola y luego trazamos la altura (amplitud) versus posición. Esto nos da la siguiente imagen de una ola congelada en el tiempo (al igual que una foto de una ola):

Figura\(\PageIndex{2}\)

El desplazamiento desde la posición de equilibrio se medirá en metros (o centímetros, etc.) al igual que en la gráfica anterior. También podemos medir la distancia horizontal de un pico a otro pero esta vez será en metros en lugar de segundos. Esta distancia se llama la longitud de onda,\(\lambda\). En la gráfica la distancia pico a pico es de\(2.5\text{ m}\) a la\(4.6\text{ m}\) que da una longitud de onda de\(4.6\text{ m} - 2.5\text{ m} = 2.1\text{ m}\) (esta es también la distancia de abajo a abajo o distancia desde donde está aumentando y tiene un desplazamiento de cero al siguiente lugar donde está aumentando y tiene un desplazamiento de cero, etc.).

Ahora imagina una larga línea de corchos flotando en la superficie de un lago. A medida que pasa una ola, el extremo más cercano de la fila de corchos comienza a moverse hacia arriba y hacia abajo y luego el resto de la fila. Cada corcho está experimentando un simple movimiento armónico (que estudiamos en el Capítulo 3) pero en una fase ligeramente diferente. Cada corcho tiene una gráfica de tiempo como la primera gráfica anterior pero tomar una foto del grupo en su conjunto da una gráfica de tiempo congelada como la segunda gráfica anterior. Las ecuaciones que describen una onda serán funciones seno y coseno, al igual que para el simple movimiento armónico que vimos en el Capítulo 3 pero ahora las variables dependerán tanto del tiempo como de la distancia (el ejercicio de simulación a continuación lo explica en detalle).

La velocidad de la onda, su frecuencia y su longitud de onda están relacionadas. Si dos ondas viajan a la misma velocidad pero tienen diferentes longitudes de onda, un corcho que flota en cada una se balanceará hacia arriba y hacia abajo a diferentes velocidades y por lo tanto tendrá diferentes frecuencias. Una longitud de onda más corta hará que el corcho se mueva con más frecuencia, mientras que una longitud de onda más larga hará que el corcho se mueva menos Matemáticamente esta relación se expresa como\(v=\lambda f\) donde\(v\) está la velocidad de la onda en metros por segundo,\(\lambda \) es la longitud de onda en metros y\(f\) es la frecuencia de la onda en Hertz. Esta ecuación se aplica a todo tipo de olas y la usaremos muchas más veces en este libro.

Ejemplos de video/audio:

• Conferencia de la Academia Kahn sobre amplitud, frecuencia, longitud de onda, 15 min.
• Conferencia de onda transversal y longitudinal.
• Conferencia de onda transversal y longitudinal.