8.2: Absorbentes; dicroísmo; polaroides
- Page ID
- 51170
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
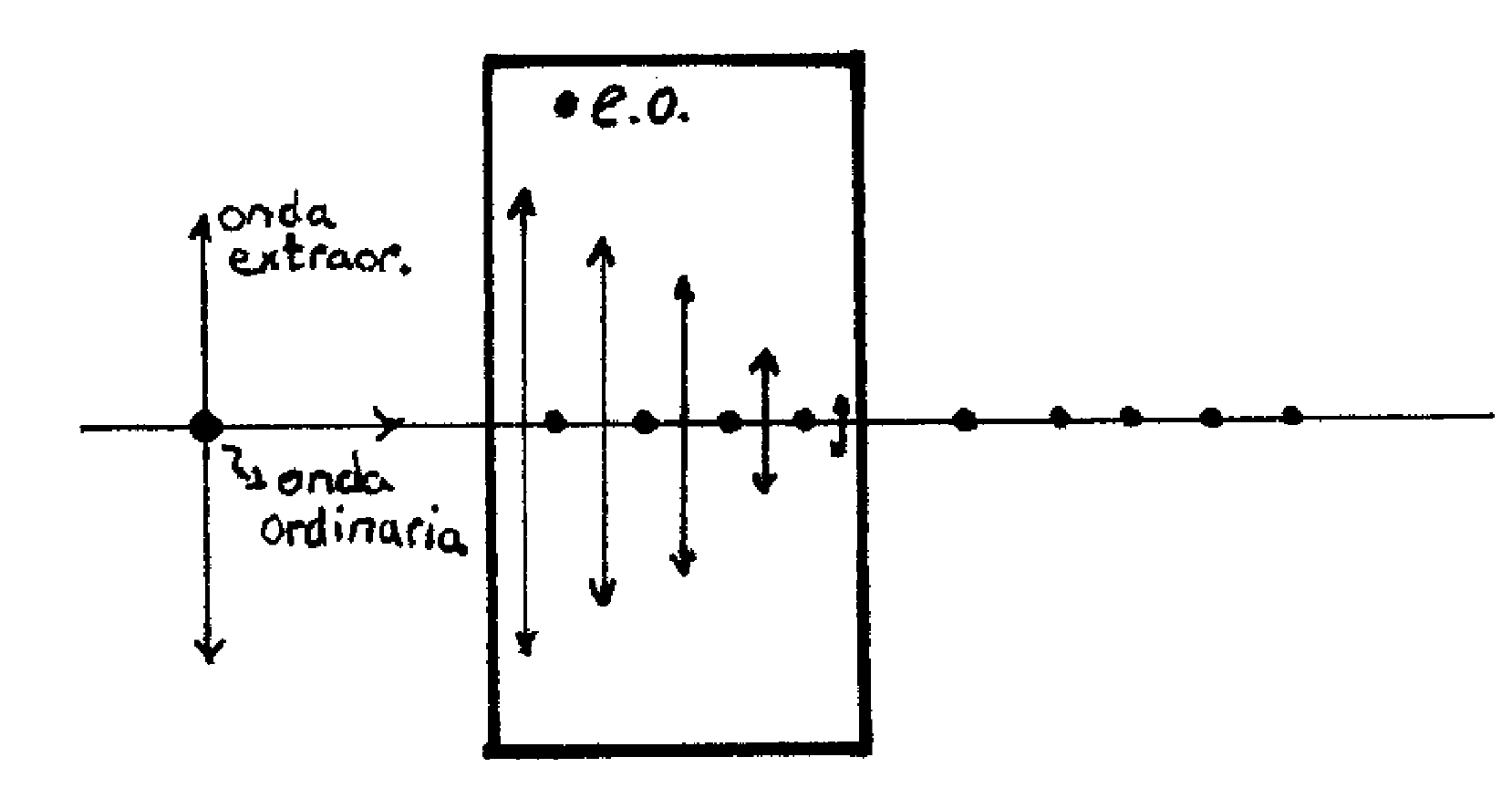
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El objetivo es obtener luz polarizada. Pensemos en un medio anisótropo uniáxico (dos constantes dieléctricas, \(\epsilon_{e}\) y \(\epsilon_{o}\) ). Podemos imaginar una situación en la cual una de estas constantes dieléctricas fuera compleja para la frecuencia de interés. Entonces el medio sería absorbente para una de las ondas y transparente para la otra. Por ejemplo
\[
\begin{aligned}
&n_{o} \rightarrow n_{o}+i \kappa_{o} \\
&n_{e} \rightarrow n_{e}
\end{aligned}
\]
con \(\kappa_{o}(\omega) \neq 0\). Este fenómeno de absorción selectiva recibe el nombre de dicroismo y los medios que producen este efecto se llaman dicroicos. Hay cristales naturales dicroicos, pero los materiales más utilizados son láminas de alcoholes de polivinilo estiradas y dopadas con yodo. La ventaja es que se pueden construirse en tamaños arbitrarios.
A partir de ahora llamaremos eje del polarizador a la dirección de vibración del haz emergente. Vamos a ver un par de ejemplos
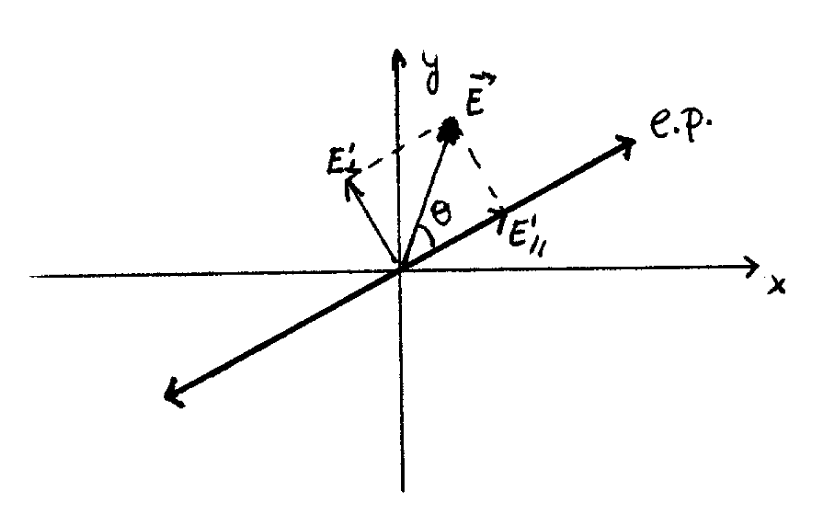
Efecto del polarizador sobre luz linealmente polarizada
El polarizador anula la componente perpendicular a su eje (absorbiéndola o refractándola en otra dirección).
\[
E_{\perp}^{\prime}=0 \notag
\]

Si el polarizador es ideal
\[
E_{\|}^{\prime}=E_{\|} \notag
\]
La intensidad del haz incidente es
\[
I \propto|\mathbf{E}|^{2} \notag
\]
y la del haz emergente
\[
I^{\prime} \propto\left|\mathbf{E}^{\prime}\right|^{2}=\left|E_{\|}^{\prime}\right|^{2}=\left|E_{\|}\right|^{2} \notag
\]
\(\operatorname{como} \cos \theta=\frac{\left|E_{\|}\right|}{|\mathbf{E}|}\) se puede escribir
\[
\begin{aligned}
&I^{\prime} \propto|\mathbf{E}|^{2} \cos ^{2} \theta \\
&I^{\prime}=I \cos ^{2} \theta
\end{aligned}
\]
la última expresión se conoce como Ley de MALUS.
Efecto del polarizador sobre luz circularmente polarizada
Para todos los ejes que escojamos la luz circular se va a escribir así:
\[
\mathbf{E} \propto\left(\begin{array}{c} \notag
1 \\
\pm i
\end{array}\right) \propto\left(\begin{array}{c}
E_{\|} \notag \\
E_{\perp}
\end{array}\right) \notag
\]
Suponiendo un polarizador ideal
\[
\begin{aligned}
E_{\|}^{\prime} &=E_{\|} \\
E_{\perp}^{\prime} &=0
\end{aligned}
\]
Las intensidades cumplen, independientemente de cómo esté colocado el eje del polarizador y, finalmente
\[
I^{\prime}=\frac{I}{2} \notag
\]
\[
\begin{aligned}
& I^{\prime} \propto\left|E_{\|}^{\prime}\right|^{2} \\
& I^{\prime} \propto\left|E_{\|}\right|^{2}+\left|E_{\perp}\right|^{2} \\
& I^{\prime} \propto 2\left|E_{\|}\right|^{2}
\end{aligned}
\]

