10.5: E- Aproximación de Stirling
- Page ID
- 128936
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
La fórmula de Stirling es una aproximación para n! eso es bueno a grandes valores de n.
\[ n !=1 \cdot 2 \cdot 3 \cdots(n-1) \cdot n\]
\[ \ln (n !)=\underbrace{\ln 1}_{0}+\ln 2+\ln 3+\cdots+\ln (n-1)+\ln (n)\]
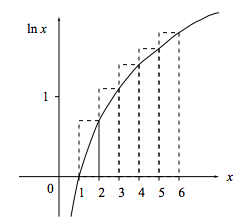
Tenga en cuenta que la función ln x es casi plana para valores grandes de x. Por ejemplo, ln 10 23 es aproximadamente igual a 23.
De la figura
\[ \ln (6 !)=\text { area under the staircase }>\int_{1}^{6} \ln x d x\]
y en general
\[ \ln (n !)>\int_{1}^{n} \ln x d x=[x \ln x-x]_{1}^{n}=n \ln n-n+1. \]
Para valores grandes de n, donde la función ln n es casi plana, las dos expresiones anteriores se vuelven bastante cercanas. Además, el 1 se vuelve despreciable. Concluimos que
\[ \ln (n !) \approx n \ln n-n \quad \text { for } n \gg 1.\]
Esta es la fórmula de Stirling. Para las correcciones a la fórmula, véase M. Boas, Métodos Matemáticos en las Ciencias Físicas, secciones 9-10 y 9-11. Ya sabes que
\[ A^n\]
aumenta rápidamente con n para A positivo, pero
\[ n ! \approx\left(\frac{n}{e}\right)^{n}\]
aumenta un poco más rápidamente aún.
E.1 Problema: Un límite superior para la función factorial
La aproximación de Stirling da un límite inferior riguroso para n!.
a. Utilizar las ideas generales presentadas en la derivación de ese límite inferior para mostrar que
\[ \int_{1}^{n} \ln (x+1) d x>\ln n !.\]
b. Concluir que
\[ (n+1) \ln (n+1)-n+1-2 \ln 2>\ln n !>n \ln n-n+1.\]


