2.4: La Primera Ley de la Termodinámica

Template:MathJaxArovas

Conservación de energía

La primera ley es una declaración de conservación de energía, y se representa en la Fig. [primera ley]. Dice, sencillamente, que durante un proceso termodinámico, el cambio en la energía interna de un sistema\(E\) viene dado por la energía térmica\(Q\) añadida al sistema, menos el trabajo\(W\) realizado por el sistema:\[\RDelta E = Q-W\ .\] La forma diferencial de esta, la Primera Ley de la Termodinámica, es\[dE=\dbar Q - \dbar W\ .\] Utilizamos el símbolo\(\dbar\) en los diferenciales\(\dbar Q\) y\(\dbar W\) para recordarnos que estos son diferenciales inexactos. La energía\(E\), sin embargo, es una función de estado, por lo tanto\(dE\) es un diferencial exacto.

Considere un volumen\(V\) de fluido mantenido en un matraz, inicialmente a temperatura\(T\ns_0\), y mantenido a presión atmosférica. La energía interna es entonces\(E\ns_0=E(T\ns_0,p,V)\). Ahora contemplemos cambiar la temperatura de dos maneras distintas. El primer método (A) consiste en colocar el matraz sobre una placa caliente hasta que la temperatura del fluido suba a un valor\(T\ns_1\). El segundo método (B) consiste en agitar el fluido vigorosamente. En el primer caso, agregamos calor\(Q\subA>0\) pero no se realiza ningún trabajo, entonces\(W\subA=0\). En el segundo caso, si aislamos térmicamente el matraz y utilizamos un agitador de muy baja conductividad térmica, entonces no se agrega calor,\(Q\subB=0\). Sin embargo, el agitador sí funciona\(-W\subB>0\) en el fluido (recuerde\(W\) es el trabajo realizado por el sistema). Si terminamos a la misma temperatura\(T\ns_1\), entonces la energía final es\(E\ns_1=E(T\ns_1,p,V)\) en ambos casos. Entonces tenemos\[\RDelta E = E\ns_1-E\ns_0 = Q\subA = -W\subB\ .\]

[primeraley] La primera ley de la termodinámica es una declaración de conservación de energía.

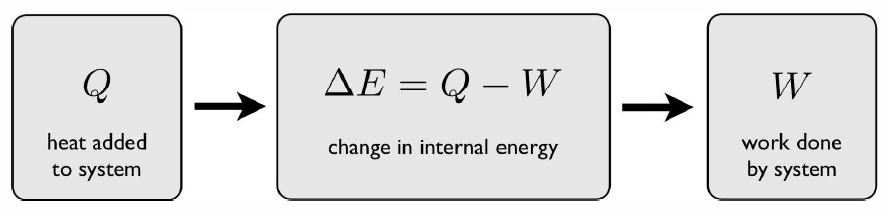
También se deduce que para cualquier transformación cíclica, donde las variables de estado son las mismas al principio y al final, tenemos\[\RDelta E\ns_{cyclic}=Q-W=0 \quad\Longrightarrow\quad Q=W \quad\hbox{(cyclic)}\ .\]

Sistemas de un solo componente

Un sistema de un solo componente se especifica mediante tres variables de estado. En muchas aplicaciones\(N\) se conserva el número total de partículas, por lo que es útil tomar\(N\) como una de las variables de estado. Los dos restantes pueden ser\((T,V)\) o\((T,p)\) o\((p,V)\). La forma diferencial de la primera ley dice\[\begin{aligned} dE&=\dbar Q-\dbar W\nonumber\\ &=\dbar Q - p\,dV + \mu\,dN\ . \label{DFL}\end{aligned}\] La cantidad\(\mu\) se llama el potencial químico. Nos preguntamos: ¿cuánto calor se requiere para hacer un cambio infinitesimal de temperatura, presión, volumen o número de partículas? Comenzamos por reescribir la Ecuación [DFL] ya\[\dbar Q=dE + p\,dV -\mu\,dN\ .\] que ahora debemos arremangarnos y hacer algún trabajo con derivadas parciales.

\(\bullet\)\((T,V,N)\)sistemas: Si las variables de estado son\((T,V,N)\), escribimos\[dE=\pabc{E}{T}{V,N}dT + \pabc{E}{V}{T,N}dV + \pabc{E}{N}{T,V}dN\ .\] Entonces\[\dbar Q=\pabc{E}{T}{V,N}dT + \Bigg[\pabc{E}{V}{T,N}+p\Bigg] dV + \Bigg[\pabc{E}{N}{T,V}-\mu\Bigg]dN\ . \label{QTVN}\]

\(\bullet\)\((T,p,N)\)sistemas: Si las variables de estado son\((T,p,N)\),\[dE=\pabc{E}{T}{p,N}dT + \pabc{E}{p}{T,N}dp+ \pabc{E}{N}{T,p}dN\ .\] escribimos También escribimos\[dV=\pabc{V}{T}{p,N}dT + \pabc{V}{p}{T,N}dp + \pabc{V}{N}{T,p}dN\ .\] Entonces\[\begin{split} \dbar Q&=\Bigg[\pabc{E}{T}{p,N}+p\pabc{V}{T}{p,N}\Bigg] dT + \Bigg[\pabc{E}{p}{T,N}+p\pabc{V}{p}{T,N}\Bigg] dp\\ &\qquad\qquad+\Bigg[\pabc{E}{N}{T,p}+ p\pabc{V}{N}{T,p} -\mu\Bigg]dN\ . \label{QTpN} \end{split}\]

\(\bullet\)\((p,V,N)\)sistemas: Si las variables de estado son\((p,V,N)\), escribimos\[dE=\pabc{E}{p}{V,N}dp + \pabc{E}{V}{p,N}dV + \pabc{E}{N}{p,V}dN\ .\] Entonces\[\dbar Q=\pabc{E}{p}{V,N}dp + \Bigg[\pabc{E}{V}{p,N}+p\Bigg] dV + \Bigg[\pabc{E}{N}{p,V}-\mu\Bigg]dN\ . \label{QpVN}\]

La capacidad calorífica de un cuerpo,\(C\), es por definición la relación entre\(\dbar Q/dT\) la cantidad de calor absorbido por el cuerpo y el cambio infinitesimal asociado en la temperatura\(dT\). La capacidad calorífica en general será diferente si el cuerpo se calienta a volumen constante o a presión constante. Ajuste\(dV=0\) da, de la Ecuación [QTVN],\[C\ns_{V,N}=\bigg({\dbar Q\over dT}\bigg)\ns_{V,N}=\pabc{E}{T}{V,N}\ . \label{cveqn}\] Del mismo modo, si establecemos\(dp=0\), entonces Ecuación [QTPn] rinde A menos que se\[C\ns_{p,N}=\bigg({\dbar Q\over dT}\bigg)\ns_{p,N}=\pabc{E}{T}{p,N}+ p \pabc{V}{T}{p,N}\ . \label{cpeqn}\] indique explícitamente lo contrario, asumiremos que\(N\) es fijo, y escribiremos\(C\ns_V\) para\(C\ns_{V,N}\) y\(C\ns_p\) para \(C\ns_{p,N}\).

[cptab] Calor específico (a\(25^\circ\,\) C, a menos que se indique lo contrario) de algunas sustancias comunes. (Fuente: Wikipedia.)

	\(c\ns_p\)	\({\tilde c}\ns_p\)		\(c\ns_p\)	\({\tilde c}\ns_p\)
SUSTANCIA	(\(\RJ/{mol}\,\RK\))	(\(\RJ/{g}\,\RK\))	SUSTANCIA	(\(\RJ/{mol}\,\RK\))	(\(\RJ/{g}\,\RK\))
Aire	29.07	1.01	\(\RH\ns_2\RO\)(\(25^\circ\,\)C)	75.34	4.181
Aluminio	24.2	0.897	\(\RH\ns_2\RO\)(\(100_+^\circ\,\)C)	37.47	2.08
Cobre	24.47	0.385	Hierro	25.1	0.450
\(\RC\RO\ns_2\)	36.94	0.839	Plomo	26.4	0.127
Diamante	6.115	0.509	Litio	24.8	3.58
Etanol	112	2.44	Neón	20.786	1.03
Oro	25.42	0.129	Oxígeno	29.38	0.918
Helio	20.786	5.193	Parafina (cera)	900	2.5
Hidrógeno	28.82	5.19	Uranio	27.7	0.116
\(\RH\ns_2\RO\)(\(-10^\circ\,\)C)	38.09	2.05	Zinc	25.3	0.387

Las unidades de capacidad calorífica son energía dividida por temperatura,\(\RJ/\RK\). La capacidad calorífica es una cantidad extensa, escalando con el tamaño del sistema. Si dividimos por el número de moles\(N/\NA\), obtenemos la capacidad calorífica molar, a veces llamada calor específico molar:\(c=C/\nu\), donde\(\nu=N/\NA\) está el número de moles de sustancia. El calor específico también se cotiza a veces en unidades de capacidad calorífica por gramo de sustancia. Vamos a definir\[{\tilde c}={C\over m N}={c\over M} = { \hbox{heat capacity per mole}\over \hbox{mass per mole}}\ .\] Aquí\(m\) está la masa por partícula y\(M\) es la masa por mol:\(M=\NA\, m\).

Supongamos que elevamos la temperatura de un cuerpo de\(T=\TA\) a\(T=\TB\). ¿Cuánto calor se requiere? Tenemos\[Q=\int\limits_\TA^\TB\!\!dT\,C(T)\ ,\] donde\(C=C\ns_V\) o\(C=C\ns_p\) dependiendo de si el volumen o la presión se mantiene constante. Para los gases ideales, como discutiremos a continuación,\(C(T)\) es constante, y por lo tanto\[Q=C(\TB-\TA) \quad\Longrightarrow\quad \TB=\TA+{Q\over C}\ .\]

En metales a temperaturas muy bajas se encuentra\(C=\gamma T\), donde\(\gamma\) es una constante ⁶. Entonces tenemos\[\begin{aligned} Q&=\int\limits_\TA^\TB\!\!dT\,C(T)=\half\gamma\big(T_\ssr{B}^2 - T_\ssr{A}^2\big)\\ \TB&=\sqrt{T_\ssr{A}^2 + 2\gamma^{-1} Q}\ .\end{aligned}\]

Gases ideales

La ecuación de estado de gas ideal es\(pV=N\kT\). Para invocar las fórmulas en Ecuaciones\ ref {QTVN},\ ref {QTPn}, y\ ref {QPVn}, necesitamos conocer la función state\(E(T,V,N)\). Un experimento histórico de Joule a mediados del siglo XIX estableció que la energía de un gas de baja densidad es independiente de su volumen ⁷. Esencialmente,\(T\) se permitió que un gas a temperatura se expandiera libremente de un volumen\(V\) a un volumen mayor\(V'>V\), sin calor agregado\(Q\) y sin trabajo\(W\) realizado. Por lo tanto, la energía no puede cambiar. Lo que Joule encontró fue que la temperatura tampoco cambió. Esto quiere decir que\(E(T,V,N)=E(T,N)\) no puede ser una función del volumen.

[CVH2] Capacidad calorífica\(C_V\) para un mol de hidrógeno (\(\RH_2\)) gas. A las temperaturas más bajas, solo los grados de libertad traslacionales son relevantes, y\(f=3\). Alrededor\(200\,\RK\), dos modos de rotación son excitables y\(f=5\). Arriba\(1000\,\RK\), las excitaciones vibracionales comienzan a contribuir. Tenga en cuenta la escala logarítmica de temperatura. (Datos de H. W. Wooley et al. , Jour. Natl. Bureau of Standards, 41, 379 (1948).)

Dado que\(E\) es extenso, concluimos que\[E(T,V,N)=\nu\,\ve(T) \ ,\] donde\(\nu=N/\NA\) está el número de moles de sustancia. Tenga en cuenta que\(\nu\) es una variable extensa. De eqns. [cveqn] y [cpeqn], concluimos\[C\ns_V(T)=\nu\,\ve'(T) \qquad,\qquad C\ns_p(T)=C\ns_V(T) + \nu R\ ,\] donde invocamos la ley ideal del gas para obtener la segunda de estas. Empíricamente se encuentra que\(C\ns_V(T)\) es independiente de la temperatura en un amplio rango de\(T\), lo suficientemente lejos del punto de ebullición. Entonces podemos escribir\(C\ns_V=\nu\, c\ns_V\), dónde\(\nu\equiv N/\NA\) está el número de moles, y dónde\(c\ns_V\) está la capacidad calorífica molar. Entonces tenemos\[c\ns_p=c\ns_V+R\ ,\] donde\(R=\NA\kB = 8.31457\,\RJ/{mol}\,\RK\) esta la constante de gas. Denotamos por\(\gamma=c\ns_p/c\ns_V\) la relación de calor específico a presión constante y a volumen constante.

A partir de la teoría cinética de los gases, se puede demostrar que\[\begin{aligned} \hbox{monatomic gases:} \quad &c\ns_V=\frac{3}{2}R\quad,\quad c\ns_p=\frac{5}{2}R \quad,\quad \gamma=\frac{5}{3}\\ \hbox{diatomic gases:} \quad &c\ns_V=\frac{5}{2}R\quad,\quad c\ns_p=\frac{7}{2}R \quad,\quad \gamma=\frac{7}{5}\\ \hbox{polyatomic gases:} \quad &c\ns_V=3R\quad,\quad c\ns_p=4R\, \quad,\quad \gamma=\frac{4}{3}\ .\end{aligned}\]

Digresión: teoría cinética de los gases

Concluiremos en general a partir de la mecánica estadística clásica no interactuante que es el calor específico de una sustancia\(c\ns_v=\half f R\), donde\(f\) está el número de coordenadas del espacio de fase, por partícula, para lo cual existe una función cinética cuadrática o de energía potencial. Por ejemplo, una partícula puntual tiene tres grados de libertad traslacionales, y la energía cinética es una función cuadrática de sus momentos conjugados:\(H\ns_0=(p_x^2 + p_y^2 + p_z^2)/2m\). Así,\(f=3\). Las moléculas diatómicas tienen dos grados rotacionales adicionales de libertad —no contamos rotaciones alrededor del eje de simetría— y sus momentos conjugados también aparecen cuadráticamente en la energía cinética, conduciendo a\(f=5\). Para las moléculas poliatómicas, los tres ángulos de Euler y sus momentos conjugados están en juego, y\(f=6\).

[CVSolid] Capacidades de calor molar\(c_V\) para tres sólidos. Las curvas sólidas corresponden a las predicciones del modelo de Debye, que discutiremos más adelante.

La razón de que\(f=5\) para las moléculas diatómicas más que\(f=6\) se debe a la mecánica cuántica. Mientras que los autoestados traslacionales forman un continuo, o se cuantifican en una caja con\(\RDelta k\ns_\alpha=2\pi/L\ns_\alpha\) ser muy pequeños, ya que las dimensiones\(L\ns_\alpha\) son macroscópicas, se cuantifica el momento angular, y por lo tanto la energía cinética rotacional. Para rotaciones alrededor de un eje principal con muy bajo momento de inercia\(I\), la escala de energía correspondiente\(\hbar^2/2I\) es muy grande, y se requiere una temperatura alta para poblar térmicamente estos estados. Así, los grados de libertad con una energía de cuantificación en el orden o mayor que\(\ve\ns_0\) se 'congelan' para temperaturas\(T\ltwid \ve\ns_0/\kB\).

En los sólidos, cada átomo está efectivamente conectado a sus vecinos por resortes; tal potencial surge de la consideración cuántica mecánica y electrostática de los átomos que interactúan. Así, cada grado de libertad contribuye a la energía potencial, y su impulso conjugado contribuye a la energía cinética. Esto da como resultado\(f=6\). Asumiendo solo vibraciones de celosía, entonces, se predice que el límite de alta temperatura\(c\ns_V(T)\) para cualquier sólido sea\(3R=24.944\,\RJ/{mol}\,\RK\). A esto se le llama la ley Dulong-Petit. El límite de temperatura alta se alcanza por encima de la llamada temperatura de Debye, que es aproximadamente proporcional a la temperatura de fusión del sólido.

En la tabla [cptab], enumeramos\(c\ns_p\) y\({\tilde c}\ns_p\) para algunas sustancias comunes en\(T=25^\circ\,\) C (a menos que se indique lo contrario). Tenga en cuenta que\(c\ns_p\) para los gases monatómicos He y Ne es de alta precisión dada por el valor de la teoría cinética,\(c\ns_p=\frac{5}{2}R=20.7864\,\RJ/{mol}\,\RK\). Para los gases diatómicos oxígeno (\(\RO\ns_2\)) y aire (mayormente\(\RN\ns_2\) y\(\RO\ns_2\)), predice la teoría cinética\(c\ns_p=\frac{7}{2}R=29.10\), que está cerca de los valores medidos. La teoría cinética predice\(c\ns_p=4R=33.258\) para gases poliatómicos; los valores medidos para\(\RC\RO\ns_2\) y\(\RH\ns_2\RO\) son aproximadamente 10% mayores.

Transformaciones adiabáticas de gases ideales

Suponiendo\(dN=0\) y\(E=\nu\,\ve(T)\), Ecuación [QTVN] nos dice que\[\dbar Q=C\ns_V\, dT + p\,dV\ .\] Invocando la ley de gas ideal para escribir\(p=\nu RT/V\), y recordando\(C\ns_V=\nu\, c\ns_V\), tenemos\(\dbar Q=0\), fijando,\[{dT\over T} + {R\over c\ns_V}\,{dV\over V}=0\ .\] podemos integrarnos inmediatamente para obtener de\[\dbar Q=0 \quad\Longrightarrow\quad\begin{cases} T V^{\gamma-1} = {constant} &\\ p V^\gamma = {constant} & \\ T^\gamma p^{1-\gamma} = {constant} & \end{cases}\] donde se obtienen las dos segundas ecuaciones el primero invocando la ley de gas ideal. Todas estas son ecuaciones adiabáticas de estado. Obsérvese la diferencia entre la ecuación adiabática de estado\(d(pV^\gamma)=0\) y la ecuación isotérmica de estado\(d(pV)=0\). Equivalentemente, podemos escribir estas tres condiciones como\[V^2\, T^f=V_0^2\, T_0^f\qquad,\qquad p^f \,V^{f+2}=p_0^f \,V_0^{f+2} \qquad,\qquad T^{f+2}\, p^{-2}=T_0^{f+2}\, p_0^{-2}\ .\]

Resulta que el aire es un conductor bastante pobre del calor. Esto sugiere el siguiente modelo para una atmósfera adiabática. La disminución de la presión hidrostática asociada a un\(dz\) aumento de altura es\(dp=-\vrh g\,dz\), donde\(\vrh\) está la densidad y\(g\) la aceleración por gravedad. Suponiendo que el gas es ideal, la densidad se puede escribir como\(\vrh=Mp/RT\), donde\(M\) está la masa molar. Así,\[{dp\over p}=-{Mg\over RT}\,dz\ .\] si los cambios de altura son adiabáticos, entonces\(d(T^\gamma p^{1-\gamma})=0\), desde, tenemos\[dT={\gamma-1\over\gamma}\,{T dp\over p}=-{\gamma-1\over\gamma}\,{Mg\over R}\,dz\ ,\] con la solución\[T(z)=T\ns_0-{\gamma-1\over\gamma}\,{Mg\over R}\,z= \bigg(1-{\gamma-1\over\gamma}\,{z\over\lambda}\bigg)\,T\ns_0\ ,\] donde\(T\ns_0=T(0)\) está la temperatura en la superficie terrestre, y\[\lambda={RT\ns_0\over Mg}\ .\] con\(M=28.88\,\Rg\) y\(\gamma=\frac{7}{5}\) para el aire, y suponiendo\(T\ns_0=293\,\RK\), encontramos\(\lambda=8.6\,\) km, y \(dT/dz=-(1-\gamma^{-1})\,T\ns_0/\lambda=-9.7\,\RK/{km}\). Tenga en cuenta que en este modelo la atmósfera termina a una altura\(z\ns_{max}=\gamma\lambda/(\gamma-1)=30\,\) km.

Nuevamente invocando la ecuación adiabática de estado, podemos encontrar\(p(z)\):\[{p(z)\over p\ns_0}=\bigg({T\over T\ns_0}\bigg)^{\gamma\over\gamma-1} = \bigg(1-{\gamma-1\over\gamma}\,{z\over\lambda}\bigg)^{\gamma\over\gamma-1}\] Recordemos que\[e^x=\lim_{k\to\infty} \Big(1+{x\over k} \Big)^{\!k}\ .\] Así, en el límite\(\gamma\to 1\), donde\(k=\gamma/(\gamma-1)\to\infty\), tenemos\(p(z)=p\ns_0\,\exp(-z/\lambda)\). Por último, ya que\(\vrh\propto p/T\) desde la ley de gas ideal, tenemos\[{\vrh(z)\over\vrh\ns_0}=\bigg(1-{\gamma-1\over\gamma}\,{z\over\lambda}\bigg)^{1\over\gamma-1}\ .\]

Expansión libre adiabática

Consideremos la situación representada en la Fig. [AFE]. Se permite que una cantidad (\(\nu\)moles) de gas en equilibrio a temperatura\(T\) y volumen\(V\ns_1\) se expanda libremente en una cámara de volumen evacuada\(V\ns_2\) mediante la eliminación de una barrera. Claramente no se realiza ningún trabajo sobre o por el gas durante este proceso, por lo tanto\(W=0\). Si las paredes están en todas partes aislantes, para que ningún calor pueda pasar a través de ellas, entonces\(Q=0\) también. La Primera Ley da entonces\(\RDelta E=Q-W=0\), y no hay cambio en la energía.

Si el gas es ideal, entonces ya que\(E(T,V,N)=N c\ns_V T\), luego\(\RDelta E=0\) da\(\RDelta T=0\), y no hay cambio de temperatura. (Si las paredes son aislantes contra el paso del calor, también deben impedir el paso de partículas, así que\(\RDelta N=0\).) Por supuesto hay un cambio en el volumen:\(\RDelta V=V\ns_2\), de ahí que haya un cambio en la presión. La presión inicial es\(p=N\kB T/V\ns_1\) y la presión final es\(p'=N\kB T/ (V\ns_1+V\ns_2)\).

[AFE] En la expansión libre adiabática de un gas, hay expansión de volumen sin trabajo ni intercambio de calor con el ambiente:\(\RDelta E = Q = W = 0\).

Si el gas no es ideal, entonces la temperatura cambiará en general. Supongamos\(E(T,V,N)=\alpha\, V^x\, N^{1-x}\, T^y\)\(\alpha\), donde\(x\),, y\(y\) son constantes. Esta forma es propiamente extensa: si\(V\) y\(N\) doble, entonces se\(E\) duplica. Si el volumen cambia de\(V\) a\(V'\) bajo una expansión libre adiabática, entonces debemos tener, de\(\RDelta E=0\),\[\bigg({V\over V'}\bigg)^{\!x} = \bigg({T'\over T}\bigg)^{\!y} \qquad\Longrightarrow\qquad T'=T\cdot\bigg({V\over V'}\bigg)^{\!x/y}\ .\] Si\(x/y>0\), la temperatura disminuye al expandirse. Si\(x/y<0\), la temperatura aumenta. Sin una ecuación de estado, no podemos decir precisamente qué sucede con la presión, aunque sabemos por motivos generales que debe disminuir porque, como veremos, la estabilidad termodinámica conlleva una compresibilidad isotérmica positiva:\(\kappa\ns_T=-{1\over V}\big({\pz V\over\pz p}\big)\ns_{T,N}>0\).

La expansión adiabática libre de un gas es un proceso espontáneo, que surge debido a la dinámica interna natural del sistema. También es irreversible. Si queremos devolver el gas a su estado original, debemos trabajar en él para comprimirlo. Si el gas es ideal, entonces las temperaturas inicial y final son idénticas, por lo que podemos colocar el sistema en contacto térmico con un reservorio a temperatura\(T\) y seguir un camino termodinámico a lo largo de una isoterma. El trabajo realizado sobre el gas durante la compresión es entonces\[\CW=-N\kT\!\int\limits_{V\ns_\Rf}^{V\ns_\Ri}\!{dV\over V} =N\kT\,\ln\!\bigg({V\ns_\Rf\over V\ns_\Ri}\bigg) = N\kT\,\ln\!\bigg(\!1 + {V\ns_2\over V\ns_1}\bigg)\] El trabajo realizado por el gas es\(W=\int\!p\, dV=-\CW\). Durante la compresión, la energía térmica\(Q=W<0\) se transfiere al gas desde el reservorio. Así,\(\CQ=\CW>0\) es desprendido por el gas a su entorno.