7.1: El sistema van der Waals

Template:MathJaxArovas

Ecuación de estado

Recordemos la ecuación de estado de van der Waals,

\[\bigg(p+{a\over v^2}\bigg)(v-b)=RT\ ,\]

donde\(v=N\ns_{\ssr{A}} V/N\) está el volumen molar. Resolviendo para\(p(v,T)\), tenemos

\[p={RT\over v-b}-{a\over v^2}. \label{pvvdw}\]

Fijemos la temperatura\(T\) y examinemos la función\(p(v)\). Claramente\(p(v)\) es una función decreciente del volumen para\(v\) justo por encima del valor mínimo permitido\(v=b\), así como para\(v\to\infty\). Pero, ¿es\(p(v)\) una función monótona para todos\(v\in [b,\infty]\)?

Podemos responder a esto calculando el derivado,

\[\pabc{p}{v}{T}=\dfrac{2a}{v^3} - \dfrac{RT}{(v-b)^2}. \label{vdwdpdva}\]

Estableciendo esta expresión a cero para finitos\(v\), obtenemos la ecuación ¹

\[{2a\over bRT}={u^3\over (u-1)^2} \ , \label{vdwdpdvb}\]

donde\(u\equiv v/b\) es adimensional. Es fácil ver que la función\(f(u)=u^3/(u-1)^2\) tiene un mínimo único para\(u>1\). \(f'(u^*)=0\)Fijando rendimientos\(u^*=3\), y así\(f\ns_{min}=f(3)=\frac{27}{4}\). Así, for\(T>T\ns_\Rc=8a/27bR\), el LHS de la Ecuación\ ref {vdwdpdvb} se encuentra por debajo del valor mínimo del RHS, y no hay solución. Esto significa que\(p(v,T>T\ns_\Rc)\) es una función monótonamente decreciente de\(v\).

En\(T=T\ns_\Rc\) hay una bifurcación de nodo de silla de montar. Fijando\(v\ns_\Rc=b u^*=3b\) y evaluando\(p\ns_\Rc=p(v\ns_\Rc,T\ns_\Rc\)), tenemos que la ubicación del punto crítico para el sistema van der Waals es

\[p\ns_\Rc={a\over 27\,b^2}\qquad,\qquad v\ns_\Rc=3b\qquad,\qquad T\ns_\Rc={8a\over 27\,bR}.\]

Para\(T<T\ns_\Rc\), existen dos soluciones a la Ecuación\ ref {vdwdpdvb}, correspondientes a un mínimo local y un máximo local de la función\(p(v)\). El locus de puntos en el\((v,p)\) plano para el cual\((\pz p/\pz v)\ns_T=0\) se obtiene estableciendo la Ecuación\ ref {vdwdpdva} a cero y resolviendo para\(T\), luego sustituyendo esto en la Ecuación\ ref {pvvdw}. El resultado es

\[p^*(v)={a\over v^2}-{2ab\over v^3}. \label{pstar}\]

Expresado en términos de cantidades adimensionales\({\bar p}=p/p\ns_\Rc\) y\({\bar v}=v/v\ns_\Rc\), esta ecuación se convierte en

\[{\bar p}^*({\bar v})={3\over{\bar v}^2} - {2\over{\bar v}^3}.\]

Figura\(\PageIndex{1}\): Presión versus volumen molar para el gas van der Waals a temperaturas en intervalos iguales de\(T=1.10\, T_\Rc\) (rojo) a\(T=0.85\,T_\Rc\) (azul). La curva púrpura es\({\bar p}^*({\bar v})\).

A lo largo de la curva\(p=p^*(v)\), la compresibilidad isotérmica,\(\kappa\ns_T=-{1\over v}\big({\pz v\over\pz p}\big)\ns_T\) diverge, anunciando una inestabilidad termodinámica. Para entender mejor, calculemos la energía libre del sistema van der Waals,\(F=E-TS\). En cuanto a la energía\(E\), volvimos a demostrar en el capítulo 2 que

\[\pabc{\ve}{v}{T}=T\pabc{p}{T}{V}-p = {a\over v^2}\ ,\]

lo que conlleva

\[\ve(T,v)=\half f RT - {a\over v}\ ,\]

donde\(\ve=E/\nu\) está la energía interna molar. El primer término es la energía molar de un gas ideal, donde\(f\) está el número de libertades moleculares, que es el límite apropiado de baja densidad. El calor específico molar es entonces\(c\ns_V=\big({\pz\ve\over\pz T}\big)\ns_v=\frac{f}{2}R\), lo que significa que la entropía molar es

\[s(T,v)=\int^T\!\!\!\! dT'\ {c\ns_V\over T'} = \frac{f}{2} R \ln(T/T\ns_\Rc) + s\ns_1(v)\ .\]

Luego escribimos\(f=\ve-Ts\), y arreglamos la función\(s\ns_1(v)\) exigiéndolo\(p=-\big({\pz f\over\pz v}\big)\ns_T\). Esto rinde\(s\ns_1(v)=R\ln(v-b)+s\ns_0\), donde\(s\ns_0\) es una constante. Así ²,

\[f(T,v)=\frac{f}{2} R \, T \, \Big( 1- \ln\!\big(T/T\ns_\Rc\big)\Big) - {a\over v} -R T \ln (v-b) - T s\ns_0\ .\]

Tabla\(\PageIndex{1}\): van der Waals parámetros para algunos gases comunes. (Fuente: Wikipedia)

gas	\(a\ \left({\RL^2\cdot{bar}\over {mol}^2}\right)\)	\(b\ \left({\RL\over{mol}}\right)\)	\(p\ns_\Rc\)(barra)	\(T\ns_\Rc\)(K)	\(v\ns_\Rc\)(\(\RL/{mol}\))
Acetona	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">14.09	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.0994	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">52.82	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">505.1	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.2982
Argón	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">1.363	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.03219	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">48.72	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">150.9	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.0966
Dióxido de carbono	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">3.640	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.04267	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">7404	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">304.0	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.1280
Etanol	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">12.18	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.08407	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">63.83	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">516.3	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.2522
Freón	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">10.78	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.0998	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">40.09	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">384.9	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.2994
Helio	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">0.03457	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.0237	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">2.279	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">5.198	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.0711
Hidrógeno	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">0.2476	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.02661	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">12.95	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">33.16	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.0798
Mercurio	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">8.200	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.01696	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">1055	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">1723	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.0509
Metano	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">2.283	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.04278	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">46.20	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">190.2	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.1283
Nitrógeno	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">1.408	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.03913	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">34.06	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">128.2	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.1174
Oxígeno	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">1.378	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.03183	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">50.37	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">154.3	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.0955
Agua	\ (a\\ izquierda ({\ RL^2\ cdot {bar}\ sobre {mol} ^2}\ derecha)\)” style="text-align:center; vertical-align:middle; ">5.536	\ (b\\ left ({\ RL\ over {mol}}\ right)\)” style="text-align:center; vertical-align:middle; ">0.03049	\ (p\ ns_\ Rc\) (bar)” style="text-align:center; vertical-align:middle; ">220.6	\ (T\ ns_\ Rc\) (K)” style="text-align:center; vertical-align:middle; ">647.0	\ (v\ ns_\ Rc\) (\(\RL/{mol}\))” style="text-align:center; vertical-align:middle; ">0.0915

Sabemos que en condiciones de equilibrio,\(f\) es impulsado al mínimo por procesos espontáneos. Ahora supongamos que\({\pz^2\! f\over\pz v^2}\big|\nd_T<0\) sobre algún rango de\(v\) a una temperatura dada\(T\). Esto significaría que un mol del sistema a volumen\(v\) y temperatura\(T\) podría disminuir su energía reordenándose en dos medios moles, con volúmenes molares respectivos\(v\pm\delta v\), cada uno a temperatura\(T\). El volumen total y la temperatura permanecen así fijos, pero la energía libre cambia en una cantidad\(\RDelta f=\half {\pz^2\! f\over\pz v^2} \big|\nd_T(\delta v)^2<0\). Esto significa que el sistema es inestable —puede bajar su energía dividiéndolo en dos subsistemas cada uno con diferentes densidades (volúmenes molares). Tenga en cuenta que el inicio de la estabilidad ocurre cuando

\[{\pz^2 \!f\over\pz v^2}\bigg|\nd_T = -{\pz p\over\pz v}\bigg|\nd_T= {1\over \>v \kappa\ns_p}=0\ ,\]

es decir cuándo\(\kappa\ns_p=\infty\). Como vimos, esto ocurre en\(p=p^*(v)\), dado en la Ecuación [pstar].

Sin embargo, esta condición\({\pz^2\! f\over\pz v^2}\big|\nd_T<0\), de hecho, es demasiado fuerte. Es decir, el sistema puede ser inestable incluso a volúmenes molares donde\({\pz^2\! f\over\pz v^2}\big|\nd_T>0\). La razón se muestra gráficamente en la Figura\(\PageIndex{2}\). A la temperatura fija\(T\), para cualquier volumen molar\(v\) entre\(v\ns_{liquid}\equiv v\ns_1\) y\(v\ns_{gas}\equiv v\ns_2\,\), el sistema puede disminuir su energía libre separando fases en regiones de diferentes volúmenes molares. En general podemos escribir

\[v=(1-x)\,v\ns_1 + x\,v\ns_2\ ,\]

así\(v=v\ns_1\) cuando\(x=0\) y\(v=v\ns_2\) cuando\(x=1\). La energía libre tras la separación de fases es simplemente

\[f=(1-x)\,f\ns_1 + x\,f\ns_2\ ,\]

donde\(f\ns_j=f(v\ns_j,T)\). Esta función viene dada por la línea negra recta que conecta los puntos en volúmenes\(v\ns_1\) y\(v\ns_2\) en la Figura \(\PageIndex{2}\).

Figura Energía libre\(\PageIndex{2}\) molar\(f(T,v)\) del sistema van der Waals\(T=0.85\,T_\Rc\), con línea negra punteada que muestra la construcción de Maxwell conectando volúmenes molares\(v_{1,2}\) en lados opuestos de la curva de coexistencia.

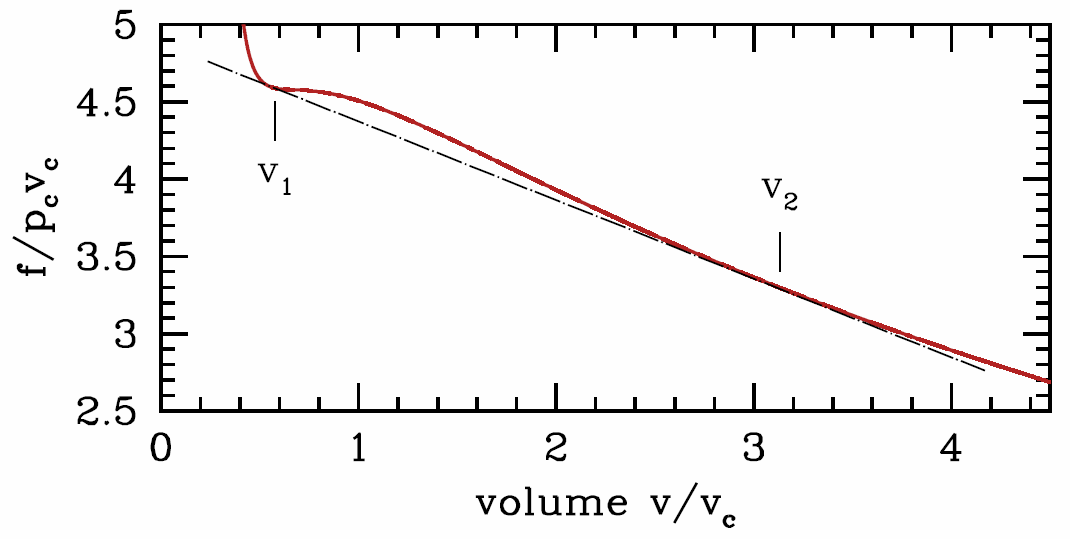
Las dos ecuaciones que nos dan\(v\ns_1\) y\(v\ns_2\) son

\[{\pz f\over\pz v}\bigg|\nd_{v\ns_1,T}=\ {\pz f\over\pz v}\bigg|\nd_{v\ns_2,T} = {f(T,v\ns_2)-f(T,v\ns_1)\over (v\ns_2-v\ns_1)}\quad.\]

Equivalentemente, en términos de la presión,\(p=-{\pz f\over\pz v}\big|\nd_T\), estas ecuaciones son equivalentes a

\[p(T,v\ns_1)=p(T,v\ns_2)= {1\over v\ns_2-v\ns_1} \int\limits_{v\ns_1}^{v\ns_2}\!\!dv\,p(T,v)\quad.\]

Este procedimiento se conoce como la construcción Maxwell, y se representa gráficamente en la Figura\(\PageIndex{3}\). Cuando se impone la construcción de Maxwell, las isotermas se asemejan a las curvas de la Figura\(\PageIndex{1}\). En esta figura, todos los puntos dentro de la región sombreada púrpura tienen\({\pz^2\!f\over\pz v^2}<0\), de ahí que esta región sea inestable a fluctuaciones infinitesimales. El límite de esta región se llama espinodal, y la separación espontánea de fases en dos fases es un proceso conocido como descomposición espinodal. La curva naranja punteada, llamada curva de coexistencia, marca el límite de inestabilidad para la nucleación. En un proceso de nucleación, se debe superar una barrera energética para lograr el menor estado de energía libre. No hay barrera energética para la descomposición espinodal — es un proceso espontáneo.

Forma analítica de la curva de coexistencia cerca del punto crítico

Escribimos\({v\ns_\SL}={v\ns_\Sc}+{w\ns_\SL}\) y\({v\ns_\SG}={v\ns_\Sc}+{w\ns_\SG}\). Una de nuestras ecuaciones es\(p({v\ns_\Sc}+{w\ns_\SL},T)=p({v\ns_\Sc}+{w\ns_\SG},T)\). Taylor expandiéndose en poderes de\({w\ns_\SL}\) y\({w\ns_\SG}\), tenemos

\[0 = p\ns_v({v\ns_\Sc},T)\,({w\ns_\SG}-{w\ns_\SL}) + \half\,p\ns_{vv}({v\ns_\Sc},T)\,\big(w_\SG^2-w_\SL^2\big)+ \frac{1}{6}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_\SG^3-w_\SL^3\big) + \ldots\ , \label{coexeqa}\]

donde

\[p\ns_v\equiv{\pz p\over\pz v} \quad,\quad p\ns_{vv}\equiv{\pz^2p\over\pz v^2} \quad,\quad p\ns_{vvv}\equiv {\pz^3p\over\pz v^3} \quad , \quad p\ns_{vT}\equiv{\pz^2p\over\pz v\,\pz T}\quad,\quad {etc.}\]

La segunda ecuación que escribimos como

\[\int\limits_{w\ns_\SL}^{w\ns_\SG}\!\!dw\>p({v\ns_\Sc}+w,T) = \half({w\ns_\SG}-{w\ns_\SL})\Big(p({v\ns_\Sc}+{w\ns_\SL},T)+p({v\ns_\Sc}+{w\ns_\SG},T)\Big)\ .\]

Expandiendo en poderes de\({w\ns_\SL}\) y\({w\ns_\SG}\), esto se convierte en

\[\begin{split} &p({v\ns_\Sc},T)\,({w\ns_\SG}-{w\ns_\SL}) + \half\,p\ns_v({v\ns_\Sc},T)\,\big(w_\SG^2-w_\SL^2\big) + \frac{1}{6}\,p\ns_{vv}({v\ns_\Sc},T)\,\big(w_\SG^3-w_\SL^3\big)\\ &\hskip1,5in + \frac{1}{24}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_\SG^4-w_\SL^4\big) + \frac{1}{120}\,p\ns_{vvvv}({v\ns_\Sc},T)\,\big(w_\SG^5-w_\SL^5\big) + \ldots \\ &\hskip0.75in=\half({w\ns_\SG}-{w\ns_\SL})\Big\{2\,p({v\ns_\Sc},T) + p\ns_v({v\ns_\Sc},T)\,({w\ns_\SG}+{w\ns_\SL}) + \half\,p\ns_{vv}({v\ns_\Sc},T)\,\big(w_\SG^2+w_\SL^2\big) \\ &\hskip1.7in +\frac{1}{6}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_\SG^3+w_\SL^3\big) + \frac{1}{24}\,p\ns_{vvvv}({v\ns_\Sc},T)\,\big(w_\SG^4+w_\SL^4\big) + \ldots\Big\} \end{split}\]

Al restar el LHS del RHS, encontramos que luego podemos dividirnos por\(\frac{1}{6}\big(w_\SG^2-w_\SL^2\big)\), resultando en

\[0=p\ns_{vv}({v\ns_\Sc},T) + \half \, p\ns_{vvv}({v\ns_\Sc},T)\,({w\ns_\SG}+{w\ns_\SL}) + \frac{1}{20} \, p\ns_{vvvv}({v\ns_\Sc},T)\, \big(3w_\SG^2+4{w\ns_\SG}{w\ns_\SL}+ 3w_\SL^2\big)+\CO\big(w^3_{\SG,\SL}\big)\ . \label{coexeqb}\]

Ahora definimos\(w\ns_\pm\equiv{w\ns_\SG}\pm{w\ns_\SL}\). En términos de estas variables, las ecuaciones\ ref {coexeqa} y\ ref {coexeqb} se convierten

\[\begin{split} 0&=p\ns_v({v\ns_\Sc},T)+\half\,p\ns_{vv}({v\ns_\Sc},T)\,w\ns_+ + \frac{1}{8}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_+^2 + \third \, w_-^2\big) + \CO\big(w_\pm^3\big)\vph\\ 0&=p\ns_{vv}({v\ns_\Sc},T) + \half \, p\ns_{vvv}({v\ns_\Sc},T)\,w\ns_+ + \frac{1}{8} \, p\ns_{vvvv}({v\ns_\Sc},T)\,\big(w_+^2 + \frac{1}{5}\,w_-^2\big) +\CO\big(w^3_\pm\big)\ . \end{split}\]

Figura\(\PageIndex{3}\): Maxwell construcción en el\((v,p)\) plano. El sistema es absolutamente inestable entre volúmenes\(v_\Rd\) y\(v_\Re\). Para\(v\in[v_\Ra,v_\Rd]\) de\(v\in [v_\Re,v_\Rc]\), la solución es inestable con respecto a la separación de fases. Fuente: Wikipedia.

Ahora evaluamos\(w\ns_\pm\) al orden\(T\). Tenga en cuenta que\(p\ns_v({v\ns_\Sc},{T\ns_\Sc})=p\ns_{vv}({v\ns_\Sc},{T\ns_\Sc})=0\), ya que el punto crítico es un punto de inflexión en el\((v,p)\) plano. Así, tenemos\(p\ns_v({v\ns_\Sc},T)=p\ns_{vT}\,\Theta+\CO(\Theta^2)\), dónde\(T={T\ns_\Sc}+\Theta\) y\(p\ns_{vT}=p\ns_{vT}({v\ns_\Sc},{T\ns_\Sc})\). Entonces podemos ver que\(w\ns_-\) es de orden principal\(\sqrt{-\Theta\,}\), mientras que\(w\ns_+\) es de orden principal\(\Theta\). Esto nos permite escribir

\[\begin{split} 0&=p\ns_{vT}\,\Theta + \frac{1}{24}\,p\ns_{vvv}\,w_-^2 + \CO(\Theta^2) \vph\\ 0&=p\ns_{vvT}\,\Theta + \half\,p\ns_{vvv}\,w\ns_+ + \frac{1}{40}\,p\ns_{vvvv}\,w_-^2 + \CO(\Theta^2)\ . \end{split}\]

Por lo tanto,

\[\begin{split} w\ns_-&=\bigg( {24\, p\ns_{vT} \over p_{vvv} } \bigg)^{\!\!1/2} \sqrt{-\Theta\,} + \ldots\vph \\ w\ns_+&=\bigg({6\,p\ns_{vT}\,p\ns_{vvvv}-10\, p\ns_{vvv}\,p\ns_{vvT}\over 5\, p_{vvv}^2} \bigg)\,\Theta + \ldots \ . \end{split}\]

Entonces tenemos

\[\begin{split} {w\ns_\SL}&=-\bigg( {6\, p\ns_{vT} \over p_{vvv} } \bigg)^{\!\!1/2} \sqrt{-\Theta\,} +\bigg({3\,p\ns_{vT}\,p\ns_{vvvv}-5\, p\ns_{vvv}\,p\ns_{vvT}\over 5\, p_{vvv}^2} \bigg) \Theta + \CO\big(\Theta^{3/2}\big)\vph \\ {w\ns_\SG}&=\bigg( {6\, p\ns_{vT} \over p_{vvv} } \bigg)^{\!\!1/2} \sqrt{-\Theta\,} +\bigg({3\,p\ns_{vT}\,p\ns_{vvvv}-5\, p\ns_{vvv}\,p\ns_{vvT}\over 5\, p_{vvv}^2} \bigg) \Theta + \CO\big(\Theta^{3/2}\big) \ . \end{split}\]

Supongamos que seguimos a lo largo de una isoterma a partir de la fase de alto volumen molar (gas). Si\(T>{T\ns_\Sc}\), el volumen\(v\) disminuye continuamente a medida que\(p\) aumenta la presión. Si\(T<{T\ns_\Sc}\), entonces en el instante la isoterma primero cruza la curva límite naranja en la Figura\(\PageIndex{4}\), hay un cambio discontinuo en el volumen molar de alto (gas) a bajo (líquido). Este cambio discontinuo es el sello distintivo de una transición de fase de primer orden. Tenga en cuenta que la discontinuidad de volumen,\(\RDelta v=w\ns_-\propto ({T\ns_\Sc}-T)^{1/2}\). Este es un ejemplo de un comportamiento crítico en el que el parámetro de orden\(\phi\), que en este caso puede tomarse como la diferencia\(\phi={v\ns_\SG}-{v\ns_\SL}\), se comporta como una ley de poder en\(\big|T-T\ns_{\!\Rc}\big|\), donde\(T\ns_{\!\Rc}\) está la crítica temperatura. En este caso, tenemos\(\phi(T)\propto ({T\ns_\Sc}-T)_+^\beta\), dónde\(\beta=\half\) está el exponente, y dónde\(({T\ns_\Sc}-T)_+\) se define para ser\({T\ns_\Sc}-T\) si\(T<{T\ns_\Sc}\) y de\(0\) otra manera. La compresibilidad isotérmica es\(\kappa\ns_T=-v/p\ns_v(v,T)\). Esto es finito a lo largo de la curva de coexistencia — sólo diverge a lo largo de la espinodal. Por lo tanto, diverge en el punto crítico, que se encuentra en la intersección de la curva espinodal y de coexistencia.

Figura Isotermas de\(\PageIndex{4}\): presión-volumen para el sistema van der Waals, como en la Figura\(\PageIndex{1}\), pero corregidas para dar cuenta de la construcción de Maxwell. El límite de la región sombreada púrpura es la línea espinodal\({\bar p}^*({\bar v})\). El límite de la región sombreada naranja es el límite de estabilidad con respecto a la separación de fases.

Es conveniente expresar la ecuación de estado y la curva de coexistencia en términos de variables adimensionales. Escribir

\[{\bar p}={p\over p\ns_\Rc}\quad,\quad {\bar v}={v\over v\ns_\Rc}\quad,\quad {\bar T}={T\over T\ns_\Rc}.\]

La ecuación de estado de van der Waals se convierte entonces

\[{\bar p} = {8{\bar T}\over 3{\bar v}-1} - {3\over {\bar v}^2} \ . \label{vdwscaled}\]

Expresando además estas cantidades adimensionales en términos de distancia desde el punto crítico, escribimos

\[{\bar p}=1+\pi\quad,\quad{\bar v}=1+\eps\quad,\quad{\bar T}=1+t\ .\]

Por lo tanto,

\[\pi(\eps,t)={8(1+t)\over 2+3\eps}-{3\over (1+\eps)^2}-1\ .\]

Tenga en cuenta que el LHS y el RHS de esta ecuación desaparecen idénticamente para\((\pi,\eps,t)=(0,0,0)\). Entonces podemos escribir

\[\eps\ns_{\SL,\SG}=\mp \bigg( {6\, \pi\ns_{\eps t} \over \pi\ns_{\eps\eps\eps}} \bigg)^{\!\!1/2} (-t)^{1/2} +\bigg({3\,\pi\ns_{\eps t}\,\pi\ns_{\eps\eps\eps\eps} - 5\, \pi\ns_{\eps\eps\eps}\,\pi\ns_{\eps\eps t}\over 5\, \pi_{\eps\eps\eps}^2} \bigg) t + \CO\big((-t)^{3/2}\big) \ .\]

Historia de la ecuación de van der Waals

La ecuación de estado de van der Waals aparece por primera vez en la tesis doctoral ³ de van der Waals de 1873, “Over de Continu ï teit van den Gas - en Vloeistoftoestand” (“Sobre la continuidad del estado gaseoso y líquido”). En su conferencia Nóbel ⁴, van der Waals escribe sobre cómo se inspiró en el tratado de Rudolf Clausius de 1857 sobre la naturaleza del calor, donde se postula que un gas de hecho consiste en partículas microscópicas zumeando a altas velocidades. van der Waals razonó que los líquidos, que resultan cuando se comprimen los gases, también consisten en 'pequeñas partículas en movimiento': “Así concibí la idea de que no hay diferencia esencial entre el estado gaseoso y el estado líquido de la materia...”

Figura [Gugg1945] 'Universalidad' de la transición líquido-gas para ocho fluidos atómicos y moleculares diferentes, de E. A. Guggenheim, J. Chem. Phys. 13, 253 (1945). Se muestra temperatura adimensional\(T/T_\Rc\) versus densidad\(\rho/\rho_\Rc=v_\Rc/v\) adimensional. La teoría de campo de van der Waals/media da\(\RDelta v =v_{gas}-v_{liquid}\propto (-t)^{1/2}\), mientras que los experimentos muestran un resultado más cercano a\(\RDelta v \propto (-t)^{1/3}\). Aquí\(t\equiv {\bar T}-1=(T-T_\Rc)/T_\Rc\) está la desviación adimensional de la temperatura con respecto al punto crítico. Imagen utilizada sin permiso.

El tratado de Clausius mostró cómo su teoría cinética del calor era consistente con la ley de Boyle para los gases (\(pV={constant}\)a temperatura fija). van der Waals reflexionó por qué esto podría fallar para la fase líquida no diluida, y razonó que había dos diferencias principales: atracción entre partículas y excluida volumen. Estas consideraciones lo llevaron a postular su famosa ecuación,

\[p={RT\over v-b}-{a\over v^2}.\]

El primer término en el RHS da cuenta de los efectos de volumen excluidos, y el segundo para las atracciones mutuas.

En el caso limitante de\(p\to\infty\), el volumen molar se aproxima\(v=b\). Por razones físicas, cabría esperar\(b=v\ns_0/\zeta\), donde\(v\ns_0=\NA\,\omega\ns_0\) está\(\NA\) multiplicado por el volumen\(\omega\ns_0\) de una sola molécula, y la fracción de empaquetamiento es\(\zeta=N\omega\ns_0/V=v\ns_0/v\), que es la relación entre el volumen molecular total y el volumen total del sistema. En tres dimensiones, la fracción de empaque máxima posible es para celosías fcc y hcp, cada una de las cuales tiene número de coordinación\(12\), con\(\zeta\ns_{max}=\frac{\pi}{3\sqrt{2}}=0.74078\). El empaque aleatorio denso da como resultado\(\zeta\ns_{drp}=0.634\). Expandiendo la ecuación de estado de VdW en potencias inversas de\(v\) rendimientos

\[p={RT\over v}+\bigg(b-{a\over RT}\bigg)\cdot{RT\over v^2} + \CO\big(v^{-3}\big)\ ,\]

y leemos del segundo coeficiente virial\(B\ns_2=\big(b-{a\over RT}\big)/\NA\). Para esferas duras,\(a=0\), y el resultado\(B\ns_2=4\omega\ns_0\) de la expansión del cúmulo de Mayer corresponde a\(b\ns_{Mayer}=4 v\ns_0\), que es mayor que el resultado de incluso el empaque de esfera regular más flojo, que para una celosía cúbica, con\(\zeta\ns_\textsf{cub}=\frac{\pi}{6}\).

Otro de los grandes logros de van der Waals fue su articulación de la ley de los estados correspondientes. Recordemos que la ecuación de van der Waals de estado, cuando se escribe en términos de cantidades adimensionales\({\bar p}=p/p\ns_\Rc\)\({\bar v}=v/v\ns_\Rc\),\({\bar T}=T/T\ns_\Rc\), y, toma la forma de Ecuación\ ref {vdwscaled}. Así, mientras que los\(b\) parámetros\(a\) y son específicos para cada fluido —ver Tabla\(\PageIndex{1}\) — cuando se escriben en términos de estas variables adimensionales escaladas, la ecuación de estado y todas sus propiedades consecuentes (la transición de fase líquido-gas) son universales.

La ecuación de van der Waals es mejor vista como semi-fenomenológica. La interacción y los efectos de volumen excluidos seguramente están presentes, pero la ecuación de van der Waals solo los captura de una manera muy aproximada. Es aplicable a los gases, donde predice con éxito características que no están presentes en los sistemas ideales (estrangulamiento). Es de uso sólo cualitativo y pedagógico en el estudio de los fluidos, cuya física esencial radica en el comportamiento de cantidades como la función de distribución de pares\(g(r)\). Como vimos en el capítulo 6, cualquier derivación adecuada de\(g(r)\) los primeros principios, una función que puede medirse en experimentos de dispersión, implica esquemas de aproximación bastante complicados para cerrar la jerarquía BBGKY. De lo contrario se debe recurrir a simulaciones numéricas como el método Monte Carlo. Sin embargo, las lecciones aprendidas del sistema van der Waals son invaluables y nos proporcionan una primera visión de lo que está sucediendo en las proximidades de una transición de fase, y cómo el comportamiento no analítico, como\(v\ns_\SG-v\ns_\SL\propto (T\ns_\Rc-T)^\beta\) con exponente no entero\(\beta\) puede resultar debido a singularidades en el libre energía en el punto crítico.